Alessandro Zaccagnini ci propone un suo “Dialogo sui numeri primi”, un esercizio di stile in cui cercherà di parlare dei numeri primi in modo interessante senza usare formule, o quasi. Nel dialogo, che qui presentiamo a puntate, o meglio “giornate”, troveremo tre personaggi presi a prestito da Galileo: Salviati, che è un copernicano (un teorico dei numeri analitico), Sagredo, che è un patrizio (un matematico di un altro settore), e Simplicio, che è un tolemaico (un dilettante). Questa è la quarta giornata, nella quale si discutono le formule per i numeri primi. Tutte le puntate le trovate sempre a questo link.

Giornata quarta, nella quale si discutono le formule per i numeri primi

Simplicio. Ieri sera, ripensando a quello che abbiamo discusso ieri mattina, mi è venuto in mente che tutti i problemi sarebbero risolti se si trovasse una formula che ci dà tutti i numeri primi.

Sagredo. O anche una formula che dà solo numeri primi, vero Salviati?

Salviati. Una formula del genere esiste già, anzi, se ne conoscono parecchie, ma paradossalmente non risolvono nessun problema!

Simplicio. Non capisco: se tu hai una formula, puoi calcolarne il valore e ottenere i numeri primi, invece di fare tutti quei calcoli di cui ci hai parlato nei giorni scorsi.

Sagredo. Simplicio, stai dimenticando il fatto che calcolare una formula richiede del tempo.

Salviati. E spazio di memoria.

Simplicio. Quindi le formule non servono?

Salviati. Le formule che si conoscono oggi hanno tutte qualche controindicazione, o per la quantità di calcoli necessari o per la quantità di memoria occupata. Non possiamo escludere che in futuro si scopra una formula che non ha queste limitazioni, ma per il momento le cose stanno cosí.

Sagredo. Salviati, ce ne descrivi una?

Salviati. La prima che mi viene in mente è la formula di Gandhi, un matematico indiano omonimo del Mahatma. Se si conoscono i primi \(n\) numeri primi, questa formula permette di calcolare il numero primo successivo.

Simplicio. Quindi mi stai dando ragione. Se conosco i numeri primi 2, 3 e 5, uso la formula di Gandhi per calcolare 7. A questo punto posso usarla con 2, 3, 5 e 7 e calcolare 11, e cosí via.

Sagredo. C’è qualche problema di complessità computazionale?

Salviati. Precisamente. Nei passaggi intermedi del calcolo della formula di Gandhi per ottenere il numero primo 7 compaiono numeri interi di 10 cifre, ed è necessario fare i calcoli esatti per trovare il risultato richiesto. Inoltre, in generale c’è da eseguire una somma con un numero di addendi che cresce esponenzialmente con \(n\).

Sagredo. Stai dicendo che la quantità di calcoli da fare supera quelli necessari nel crivello di Eratostene?

Salviati. Di gran lunga, e sono anche molto piú complicati. C’è una sproporzione enorme tra la grandezza dei risultati intermedi e quella del risultato finale.

Simplicio. Quindi è una formula del tutto inutile?

Salviati. Dal punto di vista pratico non serve a molto. Però è molto istruttiva dal punto di vista didattico, perché ci costringe a ripensare criticamente al concetto di formula, di complessità, eccetera.

Sagredo. E comunque in matematica si può imparare molto dalle dimostrazioni, anche di cose apparentemente inutili.

Salviati. Infatti, in molti casi sono piú interessanti le dimostrazioni che i teoremi …

Sagredo. Salviati, prima hai parlato di formule, al plurale. Ci puoi parlare di qualche altra formula, oltre a quella di Gandhi?

Salviati. In linea di principio, il teorema di Wilson di cui abbiamo parlato l’altro ieri permette di scrivere una formula che dà il numero dei numeri primi che non superano un certo valore \(N\), ma come dicevamo, anche quando \(N\) è molto piccolo la formula è impraticabile, per gli stessi motivi che abbiamo già discusso e cioè la presenza di risultati parziali molto grandi.

Sagredo. Stai dicendo che conviene usare il crivello, determinare tutti i numeri primi fino ad \(N\) e poi contarli?

Salviati. Rispetto alla formula a cui ho appena alluso, sí senz’altro. Ma se il tuo obiettivo è sapere esattamente quanti numeri primi ci sono fino ad un certo intero \(N\), allora ci sono altre strade, indirette, per ottenere questo risultato.

Simplicio. Cosa intendi per strade indirette, Salviati?

Salviati. Nel diciottesimo secolo, Adrien-Marie Legendre esaminò attentamente il meccanismo del crivello di Eratostene, e scoprí una formula che permette di calcolare il numero dei numeri primi che non superano un dato intero \(N\), senza doverli elencare tutti. Ancora oggi si usano varianti di questa idea per ottenere sempre nuovi record per \(N\).

Sagredo. Ci dici come funziona la formula di Legendre?

Salviati. Si basa su un principio di base della combinatoria, detto principio di inclusione-esclusione. Per dare un’idea molto semplificata, tra 1 ed \(N\) ci sono circa \(N / 2\) numeri pari, che non sono numeri primi.

Sagredo. Tranne il numero 2, che lo è.

Salviati. Precisamente. Restano circa \(N / 2\) interi, circa \(1 / 3\) dei quali sono divisibili per 3, e quindi non sono numeri primi.

Simplicio. Tranne il numero 3, che lo è.

Salviati. Esatto. Quindi, escludendo i multipli di 2 e di 3 restano circa \(N – N / 2 – N / 3 = N / 6\) interi, tra cui cercare i numeri primi. Giusto?

[Simplicio prende un foglio di carta dal tavolino davanti a sé e fa qualche calcolo]

Simplicio. Giusto!

Sagredo. [Sorride] No, sbagliato! Hai contato due volte i multipli di 6.

Simplicio. Cosa vuoi dire, Sagredo?

Sagredo. Devi fare attenzione a non dire che un gatto ha otto zampe perché ne ha due davanti, due dietro, due a destra e due a sinistra. Guarda questa figura, Simplicio.

[Sagredo mostra una figura del principio di inclusione-esclusione applicato ai multipli di 2 e 3: tre cerchi parzialmente sovrapposti, colorati in modi diversi. Il cerchio con il bordo verde indica l’insieme di tutti gli interi positivi, il cerchio rosso indica i numeri pari, il cerchio blu indica i multipli di 3.]

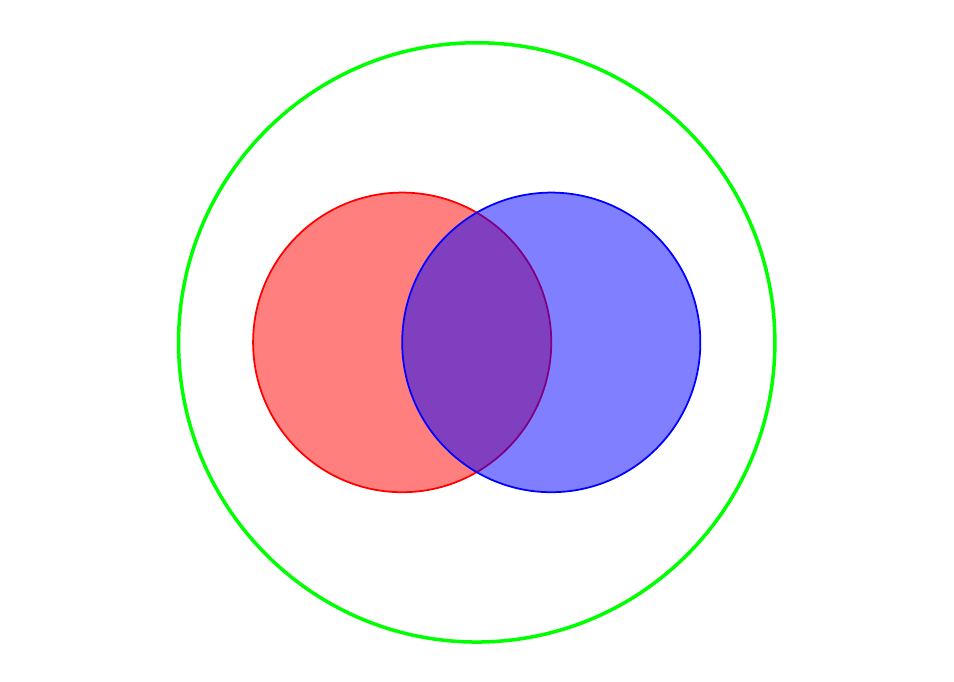
Salviati. È questo il punto del principio di inclusione-esclusione. Bisogna fare molta attenzione agli interi che sono stati “esclusi” due volte per includerli di nuovo.

Simplicio. Oltre al fatto che dobbiamo contare i numeri primi 2 e 3.

Sagredo. E che dobbiamo togliere il numero 1 che non è primo.

Salviati. Dunque, se \(N\) è grande abbiamo circa \(N – N / 2 – N / 3 + N / 6 = N / 3\) interi tra cui cercare i numeri primi.

Sagredo. Se non ho sbagliato i calcoli, questi interi residui sono quelli nelle classi di resto 1 e 5 modulo 6. Quindi 2 classi ogni 6, come dire 1 classe ogni 3, cioè un terzo degli interi.

Salviati. Precisamente. Nel disegno che hai fatto, la classe di resto 0 modulo 6 è la parte comune fra i cerchi blu e rosso; le classi di resto 2 e 4 modulo 6 sono nella parte rimanente del cerchio rosso, a sinistra; la classe di resto 3 modulo 6 è nella parte residua, a destra, del cerchio blu; infine le classi 1 e 5, come dicevi, sono dentro il cerchio con il bordo verde ma fuori dagli altri due.

Simplicio. E quindi non ci sono numeri primi dentro i cerchi rosso e blu.

Salviati. A parte i numeri 2 e 3. Discuteremo domani della distribuzione dei numeri primi nelle classi di resto.

Sagredo. Tornando alla formula di Legendre, immagino che non sia tutto qui.

Salviati. Infatti: dobbiamo ripetere lo stesso procedimento per eliminare i multipli di 5, facendo attenzione a non contare due volte i multipli di 6, 10, 15.

Sagredo. E a non contare tre volte i multipli di 30.

Salviati. E poi devi ripetere da capo per tutti i numeri primi fino alla radice quadrata di \(N\).

Sagredo. Un bel mal di testa …

[Figura del principio di inclusione-esclusione applicato ai multipli di 2, 3 e 5: quattro cerchi parzialmente sovrapposti, colorati in modi diversi. I cerchi verde, rosso e blu hanno lo stesso significato di prima, mentre il cerchio giallo indica i multipli di 5.]

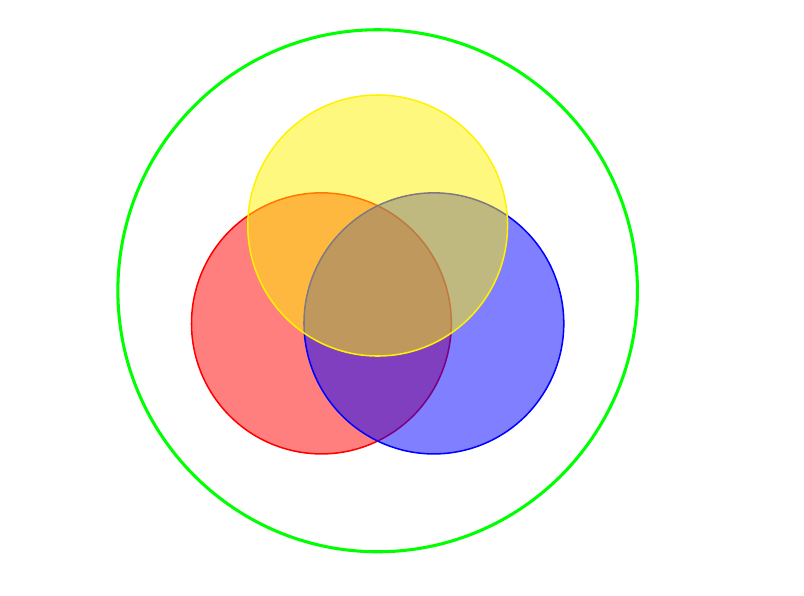
Salviati. Come vedi, non è una cosa semplicissima da realizzare, perché devi tenere conto di tutte le combinazioni possibili. Però, in questo modo si capisce che non è necessario elencare tutti i numeri primi e poi contarli, perché questo metodo indiretto permette di contarli lo stesso e ottenere il risultato voluto in un modo completamente diverso.

Sagredo. E la formula di Legendre è ancora usata per fare questi calcoli?

Simplicio. Prima che tu risponda, Salviati, qual è il record al giorno d’oggi?

Salviati. Qualche anno fa è stato portato a termine il calcolo esplicito del numero dei numeri primi fino a \(10^{27}\). La tecnica usata per i calcoli piú recenti è basata su idee sviluppate alla fine dell’Ottocento da Ernst Meissel e rielaborate da numerosi matematici nel corso dell’ultimo secolo.

Sagredo. Queste idee sono radicalmente diverse da quelle di Legendre?

Salviati. No, in fin dei conti sono sempre tecniche di natura combinatoria, in cui si contano gli elementi di certi insiemi di interi che hanno, o non hanno, dati fattori primi. Come abbiamo accennato sopra, nella formula di Legendre il numero degli addendi, da prendere talvolta con il segno piú e talvolta con il segno meno, cresce molto rapidamente, mentre nelle formule che discendono da quelle di Meissel questo problema è meno accentuato.

Simplicio. Sarebbe molto lungo l’elenco dei numeri primi fino a \(10^{27}\)?

Salviati. Se conoscessimo tutti i numeri primi individualmente avremmo bisogno di circa 25000 TB per ogni abitante della terra! Non abbiamo un elenco, non solo perché è troppo complicato calcolarlo, ma anche perché non abbiamo spazio dove scriverlo.

Sagredo. L’ora di pranzo si avvicina, e vi invito a sospendere la nostra conversazione fino a domani mattina.

Fine della quarta giornata

(L’immagine di copertina è presa da qui)

Alessandro Zaccagnini