Un eccitante prequel della Matematica del colore, attraverso la storia degli scienziati che nel diciottesimo e diciannovesimo secolo hanno dato una struttura rigorosa alla sensazione del colore. Ci regalano questo viaggio, Edoardo Provenzi, Professore all’ Université de Bordeaux e Valentina Roberti, assegnista di ricerca presso l’Università di Padova. Questo è il sesto ed ultimo episodio. Tutti gli episodi usciti li trovate in questa pagina.

Negli episodi precedenti abbiamo visto che la teoria tricromatica di Young è arrivata a una formalizzazione matematica grazie al pionieristico lavoro di Helmholtz. In questo ultimo episodio mostreremo che esiste la possibilità di inquadrare in un formalismo matematico anche la teoria dei colori opponenti di Hering, inizialmente in profondo contrasto con la teoria di Young-Helmholtz.

Ewald Hering (1834-1918) frequentò l’Università a Lipsia e fu allievo di Weber e Fechner, i padri della psicofisica come detto nell’episodio precedente. Hering fece diverse obiezioni alla teoria dei tre recettori di Young: questa era per lui inconsistente con la nostra esperienza del colore, che giudica come fondamentali quattro diverse tinte, giallo, blu, rosso e verde, in linea con la scienza romantica o Naturphilosophie (vedi episodio 3) e non era in grado di spiegare il fenomeno del contrasto di simultaneità (ovvero il fatto che la nostra percezione del colore è profondamente influenzata dal contesto nel quale il colore è immerso). Espose la sua teoria del colore in sei comunicazioni tenute tra il 1872 e il 1874 a Vienna presso l’Accademia delle Scienze, pubblicate nel 1878 in “Zur Lehre vom Lichtsinne” (letteralmente: sull’insegnamento del senso della luce).

La formulazione della sua teoria prende le mosse da alcune evidenze sulla percezione dei colori: come mai non vengono mai osservati un giallo bluastro o un rosso verdastro?

Hering propose di ordinare i colori in 4 serie (intese come quadranti del disco del colore): dal rosso al blu, dal blu al verde, dal verde al giallo e dal giallo al rosso. Ogni colore che si trova in una di queste quattro serie apparirebbe come una miscela dei colori puri che si trovano all’estremità della serie stessa. Queste quattro serie sono organizzate come colori opponenti: il giallo si oppone al blu e il rosso al verde. Vale la pena specificare che il termine “opporsi” significa qui “essere percettivamente non assimilabile”. Così come Young ipotizzò l’esistenza dei tre recettori nella retina, Hering speculò l’esistenza di tre meccanismi bipolari: giallo-blu, rosso-verde e infine bianco-nero (per dare conto delle sensazioni delle gradazioni di grigio). Si dovrà aspettare fino al 1967 per avere la comprova del fatto che questi meccanismi sono implementati da cellule che esistono realmente: si tratta delle “cellule gangliari”.

Ai tempi di Hering,  la sua teoria non era compatibile con la teoria tricromatica: tale controversia durerà diversi anni e sarà definitivamente superata solamente negli anni ‘50 del Novecento, quando gli studi sperimentali di Dorothea Jameson e Leo M. Hurvich e di Karen e Russell DeValois e A. E. Jones mostreranno evidenze sperimentali a favore di entrambe le teorie. Di fatto oggi sappiamo che la teoria tricromatica e la teoria degli opponenti di Hering non sono altro che due descrizioni parziali di quella complessa catena di eventi che provoca la sensazione del colore.

In modo sorprendente, la modellizzazione matematica della teoria di Hering annunciata all’inizio dell’episodio passa per il formalismo della meccanica quantistica. Entrare nei dettagli con poche frasi sarebbe troppo complicato, per questo ci limitiamo a presentare il concetto quantistico che rappresenta l’opposizione cromatica: l’ortogonalità. Per comprendere a cosa ci riferiamo utilizziamo un’analogia: consideriamo due rette in un piano e l’angolo più piccolo che esse definiscono. Se questo angolo è nullo, allora le due rette individuano la stessa direzione e, a mano a mano che l’angolo aumenta, le direzioni delle rette diventano più dissimili. Questo ragionamento non può andare avanti all’infinito: si arriva ben presto ad una “posizione limite”, ovvero la perpendicolarità, detta anche ortogonalità, nella quale l’ampiezza dell’angolo vale 90 gradi. Al di là di questa posizione, l’angolo più piccolo tra le rette ha infatti un’ampiezza inferiore a 90 gradi, come si può vedere nella figura sottostante.

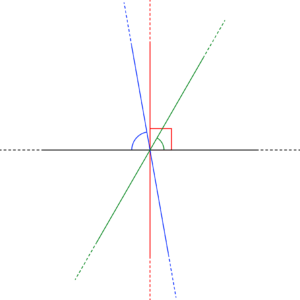
È proprio in questo senso che l’ortogonalità può essere interpretata geometricamente come la maggiore dissimilarità possibile tra le direzioni delle due rette.

In meccanica quantistica, l’ortogonalità si riferisce ai cosiddetti “stati” nei quali le osservabili di un sistema fisico possono essere misurate: la massima diversità tra due stati corrisponde proprio alla situazione in cui essi individuano due direzioni ortogonali in un opportuno spazio astratto chiamato “di Hilbert”. Il più importante risultato della recente teoria quantistica del colore mostra che ogni sensazione cromatica può essere descritta come la sovrapposizione di tre termini: il primo è uno stato quantico che rappresenta la sensazione acromatica e gli altri due sono dati dalla differenza tra due stati quantici ortogonali tra loro. Visto che i colori opponenti sono quelli che massimizzano la dissimilarità percettiva, è naturale identificarli con due stati quantistici ortogonali. Tenendo conto di questa analogia, il risultato appena citato è precisamente la scrittura della teoria dei colori opponenti di Hering nel formalismo matematico della meccanica quantistica.

Per avere più informazioni a riguardo, e per sapere quali sono le conseguenze di questa formulazione quantistica della percezione del colore, il lettore interessato può consultare, ad esempio, l’articolo disponibile gratuitamente alla pagina web seguente: https://www.mdpi.com/2313-433X/7/2/40.

Edoardo Provenzi e Valentina Roberti

#fine della serie

a cura di Barbara Nelli