Una mini-serie a cura di Gabriele Belegni, dove esploreremo i concetti principali di una delle branche più affascinanti della matematica: la topologia. Cercheremo di scoprire le motivazioni e le idee che hanno spinto ad introdurre certi concetti concentrandoci sull’aspetto intuitivo piuttosto che su quello formale. In questa puntata inizieremo a preparare gli strumenti di lavoro in topologia, costruendone l’oggetto alla base: lo spazio topologico. Trovate tutte le puntate su questa pagina.

Nella prima puntata abbiamo detto che la topologia si occupa di studiare deformazioni che non comportano strappi o cuciture. Ma come funzionano queste deformazioni? E, ancora prima, cosa vogliamo deformare? Dobbiamo capire qual è la materia prima e come lavorarla prima di provare a ricavarne qualcosa! La nostra materia prima saranno gli spazi topologici. Vi darò subito la definizione, e non preoccupatevi se vi sembrerà strana o incomprensibile, abbandoneremo subito il formalismo e risulterà tutto più sensato, promesso!

Dato un insieme \(X\), una topologia su \(X\) è una famiglia \(T\) di suoi sottoinsiemi tali che:
–  \(X \in T,\, \emptyset \in T\);
–  dato un qualunque numero, anche infinito, di elementi di \(T\), l’unione di essi è ancora un elemento di \(T\);
–  l’intersezione di un numero finito di elementi di \(T\) è ancora un elemento di\(T\);

Gli elementi di \(T\) (che sono quindi alcuni sottoinsiemi di \(X\)) sono detti aperti. Uno spazio topologico è un insieme con una topologia su di esso.

Vediamo di capire cosa significa tutto ciò. Ci concentreremo sull’aspetto intuitivo della faccenda, rinunciando parzialmente al rigore e prendendoci un po’ di libertà nell’usare termini non sempre troppo corretti, i precisi ci perdoneranno.
Uno degli strumenti fondamentali della matematica è l’insieme: insiemi di numeri, di funzioni, di persone, di oggetti… potete creare insiemi abbastanza liberamente a seconda delle vostre necessità. Dato un insieme, possiamo fare operazioni tra i suoi elementi oppure confrontarli tra di loro, ad esempio possiamo sommare o moltiplicare numeri e confrontare le altezze delle persone.
Un’altra cosa che potremmo provare a fare è dare la nozione di “vicinanza” o “lontananza” tra oggetti di un insieme, che da ora chiameremo punti. Se sapessimo misurare con precisione la distanza tra punti il gioco sarebbe presto fatto. Il problema è che non sempre siamo in grado di compiere questa misura… e poi, è veramente necessario? Per avere un’idea di “vicinanza” tra punti potremmo suddividere l’insieme in varie zone, non necessariamente disgiunte l’una dall’altra, e usarle per raggruppare questi punti. Tali zone sono l’oggetto fondamentale della topologia: gli aperti. Ad esempio, per avere un’idea di vicinanza tra studenti in una scuola potremmo raggrupparli nella varie aule in cui si trovano e dire che studenti in una stessa aula sono “vicini” tra loro.

Un aperto ci permette quindi di raggruppare gli elementi di un insieme e di generalizzare il più possibile la nozione di vicinanza o lontananza tra di essi, e notate che per far questo non serve saper misurare le distanze.
Scegliendo la struttura degli aperti riusciamo a generare una topologia sull’insieme considerato, di conseguenza a seconda della scelta fatta possiamo ottenere diverse topologie su uno stesso insieme. Prendiamo come esempio l’insieme dei punti in un piano. Come possiamo creare delle “zone”, o meglio degli aperti, che raggruppano questi punti? Qualcuno penserebbe a usare dei cerchi (che in topologia chiamiamo bocce), altri preferirebbero delle zone quadrate o, perché no, triangolari: sono tutte scelte valide e ciascuna di esse genera una topologia sul piano, rispettivamente la topologia delle bocce, dei quadrati e dei triangoli.

         
Figura 1: Confronto tra 3 topologie sul piano (disegnato come lo sfondo azzurro): a sinistra quella dei quadrati, al centro quella dei triangoli e a destra quella delle bocce.

Il termine “aperto” non è casuale, ma va inteso come un qualcosa “senza confini”, senza un bordo, insomma un qualcosa che disegnereste usando una linea tratteggiata. Il complementare di un aperto è invece detto chiuso, che come suggerisce il nome è invece ben delimitato da un bordo (che viene solitamente chiamato frontiera).

Ora, ovviamente non basta prendere un po’ di sottoinsiemi, chiamarli aperti e metterli insieme per ottenere una topologia, altrimenti ci ritroveremmo con un ammasso caotico e intrattabile: dobbiamo almeno richiedere che essi soddisfino qualche proprietà e vincolo che ci permettano di iniziare a lavorare, a dedurre risultati e teoremi, altrimenti non sapremmo da dove partire! Ecco quindi che imponiamo le tre condizioni della definizione vista sopra, che servono semplicemente ad assicurarci che uno spazio topologico sia ragionevolmente trattabile e che non si comporti in modo troppo strano, lasciandoci allo stesso tempo un’ampia libertà di movimento ed assicurandoci che questi spazi non siano troppo “rigidi” (ricordate, poi vorremmo deformare gli spazi topologici!).

Le prime due condizioni sembrano ragionevoli: tutto l’insieme deve essere un aperto, così come l’insieme vuoto, e mettendo assieme un qualunque numero (anche infinito) di aperti vogliamo avere ancora un aperto. L’ultima è un pelo più sottile: diciamo che l’intersezione di un numero finito di aperti è ancora un aperto, ma non diciamo nulla su cosa succede se intersechiamo infiniti aperti. Perché intersecare infiniti aperti dovrebbe creare problemi? L’esempio più semplice per spiegarlo è il seguente: prendete un chiuso qualsiasi \(C\) e costruite infiniti aperti che lo contengono in modo che diventino mano a mano “arbitrariamente vicini” ad esso, nel senso che tutti lo racchiudono e tendono a schiacciarsi su di esso come in figura. L’intersezione di tutti questi aperti è proprio \(C\), che però non è aperto! Ecco spiegata la motivazione della terza richiesta nella definizione.

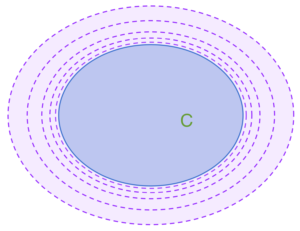
Se questo esempio intuitivo non vi convince, potete vederlo analiticamente prendendo come chiuso \(C\) l’intervallo \([0,1]\) e come aperti gli infiniti intervalli dati da \((-1/n,\ 1+1/n)\) al variare di \(n\) nei numeri naturali.

Ultima cosa, vi ricordate quel che dicevamo prima in merito a generare topologie sul piano usando bocce, quadrati o triangoli? Ecco, in un certo senso tra queste tre non c’è differenza, ossia sono topologie equivalenti: notate che ogni quadrato può essere contenuto in cerchio, così come ogni cerchio può essere messo dentro un quadrato abbastanza grande ed uno stesso discorso vale per i triangoli, quindi non ci sono differenze sostanziali tra gli aperti che vengono usati nelle tre topologie. Formalmente, diciamo che due topologie sono equivalenti se ogni aperto dell’una è contenuto in un aperto dell’altra e viceversa.

Gli spazi topologici sono quindi una struttura dove abbiamo una nozione molto generale di vicinanza e lontananza tra punti senza doverne necessariamente misurare la distanza. Sono la materia prima che stavamo cercando, non ci resta altro da fare che capire come lavorarli, come deformarli: lo strumento che useremo saranno gli omeomorfismi… ma si è fatto tardi, ve ne parlerò nella prossima puntata!

2 – continua

Gabriele Belegni

Gabriele Belegni, laureato in Matematica teorica e studente magistrale in Matematica applicata presso l’Università di Camerino. Mi occupo anche della divulgazione matematica nelle sue varie forme: articoli, conferenze e laboratori.