Presentiamo un progetto realizzato da Alessandro Zaccagnini con le docenti Maria Chiara Gullo e Lorenza Serventi in due classi dell’Istituto Comprensivo “Guatelli” di Collecchio (Parma) nel quale abbiamo preso alcuni elementi di un laboratorio svolto nell’ambito del Piano Nazionale Lauree Scientifiche nel Liceo Classico “G.B. Romagnosi” di Parma. L’obiettivo finale è dare una dimostrazione “combinatoria” del Piccolo Teorema di Fermat mediante la costruzione di piccoli gioielli.
1. Descrizione del progetto
Questo progetto prende spunto dall’articolo pubblicato nella rivista Archimede di Caterina Cozzani, Roberta Sandri e dell’Autore [1 ]C. Cozzani, R. Sandri, A. Zaccagnini, “Collane, orecchini e scatolette — Costruzione di oggetti matematici con materiali della vita quotidiana.” Archimede 1 (2024) 2–19., nel quale, prendendo spunto a nostra volta dall’articolo [2 ]A. Zaccagnini, “Collane, orecchini e …numeri.” Sito Web MaddMaths! (2022a) https://maddmaths.simai.eu/divulgazione/collane-e-orecchini/. e dai video divulgativi [3 ]A. Zaccagnini, “Il Piccolo Teorema di Fermat.” Video-pillola su YouTube (2021). e [4 ]A. Zaccagnini, “La Dimostrazione Combinatoria Del Teorema Di Wilson.” Video-pillola su YouTube (2022b)., descriviamo un laboratorio tenuto nel Liceo Classico “G.B. Romagnosi” di Parma nell’anno scolastico 2022–2023, nell’ambito del Piano Nazionale Lauree Scientifiche. Una parte di questo laboratorio, descritta in dettaglio nel §3 dell’articolo citato sopra, è stata dedicata alla dimostrazione combinatoria del Piccolo Teorema di Fermat e del Teorema di Wilson. Esistono diverse dimostrazioni tradizionali di questi risultati, che sono insegnati solitamente nel corso di “Algebra” nel primo anno del corso di studi in Matematica; per esempio il Piccolo Teorema di Fermat di cui parliamo qui si dimostra molto semplicemente per induzione usando una proprietà del triangolo di Tartaglia. Le dimostrazioni che abbiamo scelto, invece, si basano sulla costruzione di alcuni piccoli oggetti (orecchini e collane o spillette): non è difficile calcolare il numero esatto degli oggetti costruiti ma poi questi sono suddivisi in famiglie di cui è nota la cardinalità e, confrontando i due risultati, si ottiene la dimostrazione cercata. Invitiamo a guardare i video citati sopra per i dettagli.
Il progetto descritto nell’articolo di C. Cozzani, R. Sandri, e dell’Autore è stato presentato dagli stessi studenti che lo hanno realizzato in varie occasioni, l’ultima delle quali è stata la Notte dei Ricercatori del 29 settembre 2023, e dall’Autore nell’ambito di Lucca Comics & Science, 2 e 3 novembre 2023. Proprio in occasione di queste presentazioni ci sono stati i primi contatti fra l’Autore e le docenti coinvolte nel progetto presentato qui, nel quale abbiamo riprodotto in parte, in alcune classi di Scuola Secondaria di primo grado, l’esperienza delle dimostrazioni combinatorie, ma ribaltando la prospettiva utilizzata nel Liceo Classico. Infatti non abbiamo ritenuto opportuno cominciare dalla dimostrazione di un Teorema, cosa che non avrebbe particolarmente interessato gli studenti e le studentesse, ma abbiamo preferito presentare questi argomenti partendo da un problema di realtà: i piccoli gioielli descritti sopra sono costruiti con perline e altri oggetti di bigiotteria; la domanda che facciamo, dunque, è: quante perline dobbiamo comprare per realizzarli tutti, e quanti ne deve costruire ciascuno studente?
2. Sviluppo
La dimostrazione combinatoria del Piccolo Teorema di Fermat si può riassumere in questo modo. Sia \(a\) un intero positivo e \(p\) un numero primo; costruiamo le collane che hanno esattamente \(p\) perline scelte fra \(a\) colori diversi. Queste sono in totale \(a^p\) perché le scelte delle perline nelle varie posizioni sono indipendenti. Tra queste collane ce ne sono esattamente \(a\) che sono monocromatiche, cioè hanno le perline tutte dello stesso colore. Le altre possono essere suddivise in famiglie di collane equivalenti per rotazione delle perline; ogni famiglia contiene esattamente \(p\) collane (è qui che si usa l’ipotesi che \(p\) sia un numero primo) e quindi \(p\) divide \(a^p – a\). Questa dimostrazione, con spillette al posto delle collane per motivi che spieghiamo sotto, è illustrata nelle Figure 3 e 4; la scelta di costruire spillette invece di collane è legata alla facilità di realizzazione, tenendo conto del numero di esemplari necessari. La stessa scelta è stata fatta nel laboratorio originale, descritto nell’articolo già citato.
Come detto sopra, raggiungere questa dimostrazione è l’obiettivo finale, che è stato “nascosto” a studenti e studentesse fino all’ultimo, cosí come le applicazioni di cui parliamo nel §3. Il nostro lavoro è stato suddiviso in tre fasi: i dettagli pratici di come abbiamo proceduto sono descritti nel §5, dedicato al diario delle attività.
2.1 Pianificazione
La domanda che abbiamo posto è questa: vogliamo realizzare tutte le collane descritte sopra. Se ogni collana ha \(n\) perline (in questa fase non è necessario che questo sia un numero primo) e possiamo scegliere fra \(a\) colori diversi, quante sono le collane che dovremo costruire? Studenti e studentesse devono riconoscere che il numero in questione vale \(a^n\), perché ogni perlina può essere scelta in modo indipendente da tutte le altre.
Per realizzare questa fase senza rivelare niente della seconda, le docenti hanno preparato alcune centinaia di carte colorate in cartoncino di 4 colori diversi, e una griglia come quella in alto nella Figura 1, nella quale riportare tutte le possibili disposizioni con ripetizione di due, tre o quattro colori, in tre o quattro posizioni diverse, utilizzando le matite colorate che avevano con loro.

Figura 1. La griglia nella quale riportare le disposizioni trovate, colorando i pallini vuoti. Ogni gruppo di due studenti aveva a disposizione un foglio con alcune decine di righe come quella in alto. In basso una possibile colorazione, corrispondente alla scelta di una carta rossa, una blu e due verdi, in questo ordine.
Studenti e studentesse, suddivisi in gruppi di due elementi ciascuno, hanno dapprima proceduto a caso, poi hanno lentamente realizzato la necessità di trovare un metodo per assicurarsi di non tralasciare nessuna combinazione e di evitare duplicati. Qualcuno ha effettivamente riscoperto le formule che danno il numero totale di disposizioni di questo tipo, come funzione del numero dei colori a disposizione e del numero di posizioni.
Volendo suggerire un problema analogo, possiamo proporre di calcolare il numero di diverse targhe che si possono avere, o il numero di numeri telefonici, … Una possibile interpretazione formale di questa costruzione è proposta nel §3.3; si veda anche la Figura 2.

Figura 2. Le spillette con 4 perline di due colori diversi corrispondono ai numeri interi tra 0 e \(15 = 2^4 – 1\) scritti in base 2 se interpretiamo il colore rosso con la cifra 0 e il colore verde con la cifra 1. La seconda spilletta a sinistra corrisponde a 0001, cioè 1, la penultima a 1110, cioè 14, scritti in base 2. Possiamo usare questa interpretazione per suddividere in modo efficiente e a prova di errore le spillette da costruire fra i vari gruppi di studenti, assegnando a ciascun gruppo le spillette che “cominciano” con un dato colore. Abbiamo indicato in alto l’anellino che hanno le spillette in commercio per un motivo che sarà spiegato nel testo.
In questa fase studenti e studentesse devono arrivare alla scelta di valori plausibili per \(a\) ed \(n\), tenendo conto del fatto che alla fine dovranno effettivamente realizzare gli oggetti. A questo punto è necessario rivelare che \(n\) deve essere un numero primo; scelte ragionevoli per la coppia \((p, a)\) sono \((3, 4)\), \((3, 5)\), \((5, 3)\), \((7, 2)\), \((11, 2)\). Dal punto di vista estetico, consiglio di prendere \(a\) relativamente grande e quindi \(p\) relativamente piccolo. A studenti e studentesse deve essere chiesto quanti oggetti dovranno costruire a testa per ottenere il numero richiesto.
2.2 Progettazione
Una volta scelti i valori di \((p, a)\) è necessario disegnare tutti i gioielli che saranno costruiti: il numero totale è noto ed è necessaria una qualche strategia per assicurarsi di non lasciar fuori nessun elemento dell’insieme. L’interpretazione descritta sotto nel §3.3 permette di procedere in modo ordinato e di assegnare ad ogni studente o gruppo di studenti un insieme ben definito di oggetti da disegnare e poi costruire. La Figura 3 mostra il caso in cui \(p = 3\) ed \(a = 4\).

Figura 3. Le spillette con 3 perline di quattro colori diversi corrispondono ai numeri interi tra 0 e \(63 = 4^3 – 1\) scritti in base 4 se interpretiamo il colore rosso con la cifra 0 e il colore verde con la cifra 1, il colore blu con la cifra 2 e il colore giallo con la cifra 3. Queste spillette si suddividono in modo naturale in 4 gruppi da 16, guardando il colore della sola prima perlina, oppure in otto gruppi da 8, guardando alla prima e alla seconda (che può essere di due colori diversi in ciascun gruppo).
2.3 Costruzione
In questa fase si costruiscono gli oggetti progettati nel punto precedente, con studenti e studentesse divisi nei gruppi che hanno scelto. È necessario verificare che le spillette costruite siano nel numero previsto e siano tutte diverse fra loro. È ragionevole realizzare due copie di ogni spilletta in modo da avere un pannello come quello nella Figura 3 e un altro come quello nella Figura 4.
3 Applicazioni
3.1 Dimostrazione del Piccolo teorema di Fermat
Una volta realizzati tutti gli oggetti descritti nel paragrafo precedente, si possono usare per dimostrare il cosiddetto Piccolo Teorema di Fermat, a cui abbiamo accennato prima. La dimostrazione è illustrata nella Figura 4: disponiamo le spillette nella Figura 3 in classi. Nella prima poniamo quelle monocromatiche, cioè con tutte le perline dello stesso colore; queste sono esattamente 4, oppure \(a\) nel caso generale. Le altre, che sono \(4^3 – 4 = 60\) o in generale \(a^p – a\), sono disposte in “famiglie” che contengono esattamente \(3\) (cioè \(p\)) elementi ciascuna. Ogni spilletta si trova nella classe che si ottiene mediante una permutazione ciclica delle perline: questa permutazione ha periodo \(p\) o un suo divisore; ma il periodo può essere 1 solo se tutte le perline hanno lo stesso colore (cioè per le spillette monocromatiche) e altrimenti vale \(p\). È questo il punto in cui si usa l’ipotesi che \(p\) sia un numero primo e che quindi non abbia divisori propri. In definitiva, le \(a^p – a\) spillette policrome sono suddivise in classi contenenti \(p\) spillette ciascuna e quindi \(p\) divide \(a^p – a\).
3.2 Numeri decimali periodici
Questo Teorema è alla base della periodicità dello sviluppo decimale delle frazioni; si vedano anche [5 ]A. Zaccagnini, “La calcolatrice e le sue limitazioni.” L’Educazione Matematica, Anno XXVII, Serie VII 2 (2007) 35–45. e il §2.3 di [6 ]A. Zaccagnini, “Riesame critico delle operazioni elementari.” In Uno sguardo matematico sulla realtà — Laboratori PLS 2010–2014, a cura di M. Belloni e A. Zaccagnini, 71–91 (2014). Università di Parma: Dipartimento di Matematica e Informatica.. Possiamo illustrare questo fatto con un esempio: se \(p = 7\) ed \(a = 10\) allora \(7\) divide \(10^7 – 10 = 9\,999\,990\), e quindi \(7\) divide \(999\,999 = 7 \cdot 142\,857\) e questo implica che \[\frac17
=
0.\overline{142857},\] perché quando eseguiamo la divisione in colonna dopo 6 iterazioni troviamo di nuovo il resto 1, e il procedimento continua con periodo 6. Infatti, quanto detto significa che \(10^6 = 7 \cdot 142857 + 1\).
3.3 Rappresentazione in basi diverse da 10
Se \(a = 2\), le collane rappresentano i numeri interi da 0 a \(2^n – 1\) scritti in base 2. Analogamente, per \(a \ge 2\) le collane rappresentano i numeri interi da 0 ad \(a^n – 1\) scritti in base \(a\). In altre parole, stiamo rappresentando i numeri interi di \(n\) cifre o meno. Si veda la Figura 2 qui sopra per una versione esplicita della corrispondenza.

Figura 4. Le spillette della figura precedente, suddivise nelle classi che dimostrano il Teorema di Fermat.
4 I materiali
4.1 Gli oggetti costruiti
Le spillette sono state realizzate concretamente utilizzando spille da balia di dimensione opportuna e perline colorate da bigiotteria. Si tratta di materiali poco costosi e facilmente reperibili in quantità adeguata.
4.2 Materiali di partenza
Come accennato, il punto di partenza per questo laboratorio è stato l’articolo di C. Cozzani, R. Sandri e dell’Autore [7 ]C. Cozzani, R. Sandri, A. Zaccagnini, “Collane, orecchini e scatolette — Costruzione di oggetti matematici con materiali della vita quotidiana.” Archimede 1 (2024) 2–19., dove, fra le molte altre cose, trattiamo alcune dimostrazioni combinatorie della Teoria Elementare dei Numeri, per le quali si vedano anche [8 ]A. Zaccagnini, “Collane, orecchini e …numeri.” Sito Web MaddMaths! (2022a) https://maddmaths.simai.eu/divulgazione/collane-e-orecchini/., [9 ]A. Zaccagnini, “Il Piccolo Teorema di Fermat.” Video-pillola su YouTube (2021). e [10 ]A. Zaccagnini, “La Dimostrazione Combinatoria Del Teorema Di Wilson.” Video-pillola su YouTube (2022b)..
5 Diario
Qui descriviamo la prima realizzazione in assoluto di questa esperienza, in collaborazione con le docenti Maria Chiara Gullo e Lorenza Serventi dell’Istituto Guatelli di Collecchio, in provincia di Parma.
5.1 Primo incontro: 14 marzo 2024, presso DSMFI
Nel primo incontro ragazzi e ragazze hanno dovuto pianificare l’attività, senza sapere qual era il nostro obiettivo intermedio (la realizzazione delle spillette descritte sopra) né tantomeno l’obiettivo finale della dimostrazione del Piccolo Teorema di Fermat. Come detto sopra, le docenti hanno preparato alcune centinaia di carte colorate in cartoncino di 4 colori diversi, e la griglia nella Figura 1. Studenti e studentesse sono stati suddivisi in gruppi di due elementi ciascuno; dopo una fase in cui hanno proceduto a caso, hanno trovato un metodo che ha permesso loro non solo di assicurarsi di non tralasciare nessuna combinazione e di evitare duplicati ma anche, in qualche caso sporadico, di scoprire le formule che danno il numero totale di disposizioni di questi tipo, come funzione del numero dei colori a disposizioni e del numero di posizioni.

Le carte colorate

Una fase del lavoro
Una fase intermedia è stata affidata al lavoro in classe: una volta scelto il numero dei colori, cioè 4, e delle posizioni, 3, i ragazzi hanno preparato lo schema relativo, come nella nostra Figura 3.
5.2 Secondo incontro: 11 aprile 2024, presso l’Istituto Guatelli
In questa fase ragazzi e ragazze hanno provveduto alla realizzazione concreta dei gioielli: per prima cosa abbiamo rivelato quale fosse l’attività pratica che avrebbero dovuto svolgere. Abbiamo proiettato su uno schermo la Figura 3 e suddiviso studenti e studentesse (una ventina per ciascuna classe) in 8 gruppi, a ciascuno dei quali abbiamo assegnato 8 spillette da realizzare in duplice copia, usando le perline fornite all’inizio della lezione. È importante che le spillette siano fatte come in figura, con tutti gli anellini in alto.

Come usare il progetto per realizzare gli orecchini.
Al termine del lavoro, ho chiamato i vari gruppi che hanno portato su un tavolo al centro dell’aula le spillette realizzate, in un esemplare ciascuna; queste sono state disposte su un cartoncino e fissate con un filo passante per gli anellini e poi con del nastro adesivo trasparente.
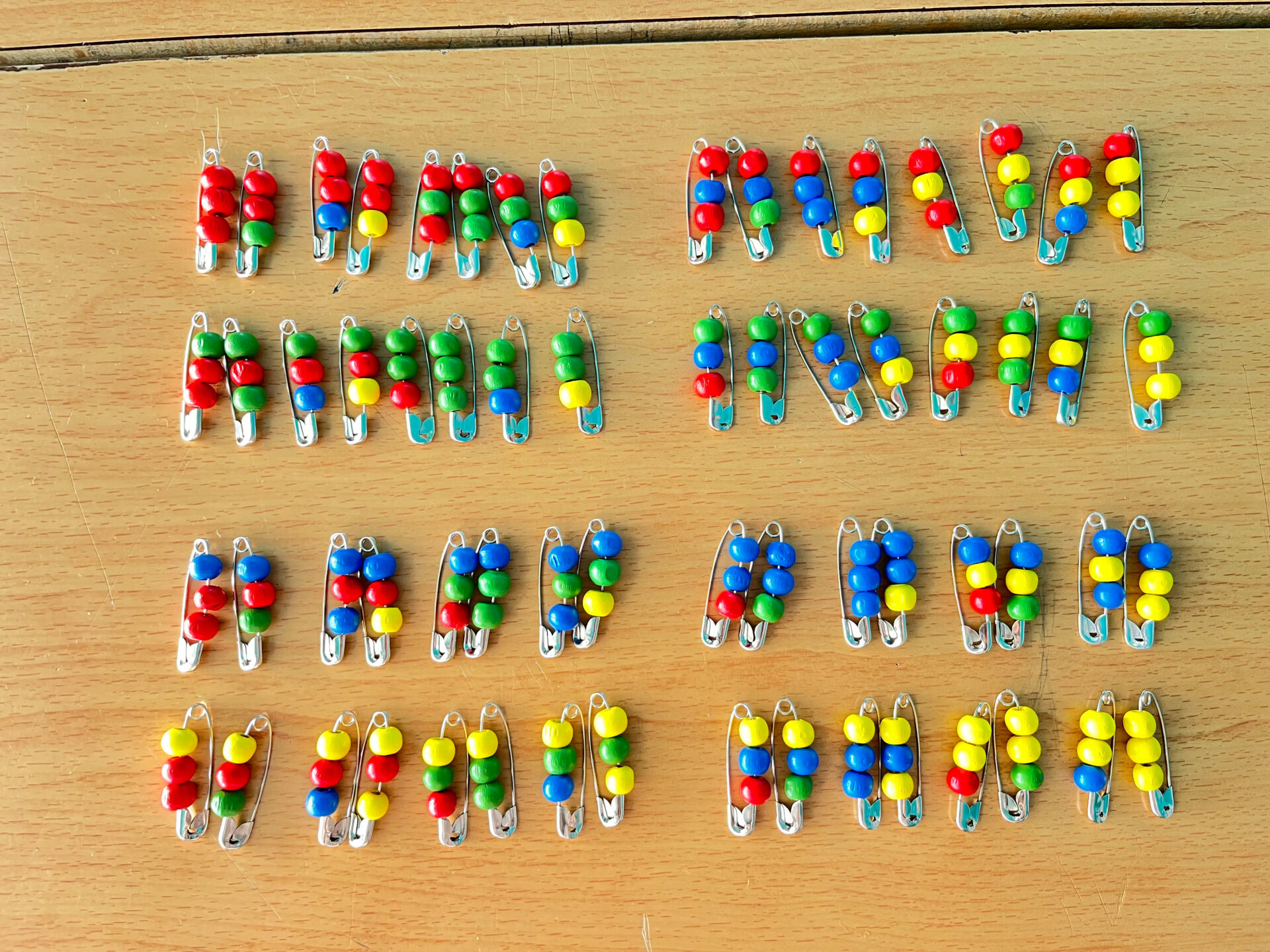
Gli orecchini del primo pannello, come nella Figura 3.
Una volta fatto questo abbiamo proiettato la Figura 4 e ho chiamato di nuovo le spillette nell’ordine dato da questa figura. Questa fase è stata piú caotica perché i gruppi sono chiamati in un ordine quasi casuale. Le spillette, disposte come in figura, sono state appoggiate su un altro cartoncino e fissate come descritto sopra.
6 Conclusioni e ringraziamenti
Studenti e studentesse mostrano di aver particolarmente apprezzato la possibiltà di passare una mattinata al Campus Universitario a sud di Parma, che molti di loro non avevano mai visto prima pur vivendo ad una decina di chilometri di distanza. Il primo incontro è stato abbinato ad una visita della “Mostra di Pitagora” e le due classi si sono alternate fra le due attività. Le docenti sottolineano come anche coloro che solitamente mostrano meno interesse per la matematica abbiano partecipato mettendosi in gioco come tutte le altre persone.
Ringraziamenti.
Ringrazio sentitamente le docenti Maria Chiara Gullo e Lorenza Serventi per l’aiuto fornito, e studenti e studentesse che hanno partecipato, per l’entusiasmo con cui hanno accettato di stare al nostro gioco.
Note e riferimenti
| ⇧1 | C. Cozzani, R. Sandri, A. Zaccagnini, “Collane, orecchini e scatolette — Costruzione di oggetti matematici con materiali della vita quotidiana.” Archimede 1 (2024) 2–19. |
|---|---|
| ⇧2, ⇧8 | A. Zaccagnini, “Collane, orecchini e …numeri.” Sito Web MaddMaths! (2022a) https://maddmaths.simai.eu/divulgazione/collane-e-orecchini/. |
| ⇧3, ⇧9 | A. Zaccagnini, “Il Piccolo Teorema di Fermat.” Video-pillola su YouTube (2021). |
| ⇧4, ⇧10 | A. Zaccagnini, “La Dimostrazione Combinatoria Del Teorema Di Wilson.” Video-pillola su YouTube (2022b). |
| ⇧5 | A. Zaccagnini, “La calcolatrice e le sue limitazioni.” L’Educazione Matematica, Anno XXVII, Serie VII 2 (2007) 35–45. |
| ⇧6 | A. Zaccagnini, “Riesame critico delle operazioni elementari.” In Uno sguardo matematico sulla realtà — Laboratori PLS 2010–2014, a cura di M. Belloni e A. Zaccagnini, 71–91 (2014). Università di Parma: Dipartimento di Matematica e Informatica. |
| ⇧7 | C. Cozzani, R. Sandri, A. Zaccagnini, “Collane, orecchini e scatolette — Costruzione di oggetti matematici con materiali della vita quotidiana.” Archimede 1 (2024) 2–19. |























