In quanti modi posso fare ambo al gioco del Lotto? In quanti modi possono ricadere due dadi lanciati in aria? Quante sono le possibili schedine del totocalcio? Quante strette di mano ci saranno tra cinque amici che s’incontrano? Sono domande a cui risponde il Calcolo Combinatorio. Conoscere le risposte ci aiuta a saper scegliere in modo consapevole e, soprattutto, a non rovinarci al gioco! Anna Cerasoli, matematica, insegnante, scrittrice, divulgatrice, ci propone una piccola introduzione in tre puntate a questa parte della matematica, così semplice e spesso divertente, che però trova poco spazio nei programmi didattici. Tutte le puntate le ritrovate raccolte in questa pagina.

Come programmato, in questa terza parte incontreremo due nuovi modelli:

Alcuni quadri da scegliere
Pasticcini a volontà

Nell’articolo precedente abbiamo studiato quanti sono i modi di disporre 3 quadri su una parete, scegliendoli da 5:

\(5\times 4\times 3=60\)

Tale prodotto ci ha fornito, per ogni terna scelta dai cinque di partenza, i diversi modi di ordinare i quadri sulla parete. Nel modello che stiamo per presentare, invece, siamo interessati soltanto a contare quante diverse terne, cioè quanti diversi sottoinsiemi di 3 quadri, si hanno a partire da un insieme che ne contiene 5. Infatti vogliamo solo scegliere i quadri, non appenderli. Ne deduciamo che basterà dividere il calcolo già fatto per le tutte permutazioni dei 3 quadri. Dunque:

\(\Large \frac{(5)_3}{3!}\)

Facile da ricordare: tanti fattori al numeratore quanti al numeratore!

\(\Large \frac{5\times 4\times 3}{3\times 2\times 1}=10\)

Parlando in generale: se abbiamo un insieme con n elementi e vogliamo conoscere quanti sono i suoi sottoinsiemi che ne contengono k basterà fare la seguente divisione:

\(\Large \frac{(n)_k}{k!}\)

I matematici la riassumono con questo simbolo

\(\Large\left(\begin{array}{c} n\\ k \end{array}\right)\)

chiamato coefficiente binomiale, termine che il lettore capirà più avanti, nel corso degli studi. Ecco subito un dolce esempio: in quanti diversi modi posso servirmi da un piatto con 6 pasticcini se ho deciso di mangiarne solo 2?

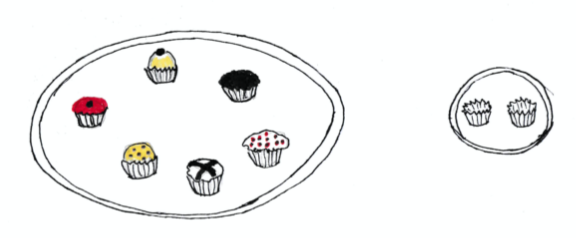
\(\Large \frac{6\times 5}{2\times 1}=15\)

Posso servirmi in 15 modi diversi. Senza fare calcoli, ma riconoscendo che si tratta dello stesso modello e degli stessi dati, so già che sono 15     anche i diversi modi di accendere solo 2 delle 6 lampade di questo ingresso.

La matematica, infatti, ha questa caratteristica: più che ai particolari è interessata alla forma generale del problema, vuole sempre vedere la forma del problema, per poi costruire la formula.

Ma torniamo ai pasticcini e facciamo il caso di un vassoio che ne contenga 4

Questa volta vogliamo studiare tutti i diversi modi di servirsi: da non prenderne alcuno a prenderli tutti. Ecco qui lo schema

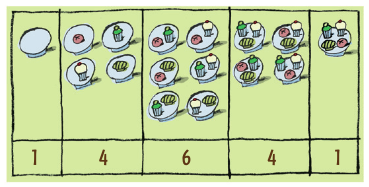
1 4 6 4 1

Una bella sequenza che potremmo definire palindroma! Non è un caso: infatti, come c’è 1 solo modo per prendere zero pasticcini, c’è 1 solo modo per prenderli tutti. Con lo stesso ragionamento si comprende che per ogni pasticcino che prendo ne restano tre, quindi il numero di modi di servirsi di 1 solo pasticcino è uguale al numero di modi di prenderne 3. Generalizziamo il problema e costruiamo il Triangolo di Tartaglia, uno strumento utilissimo per risolvere molti problemi:

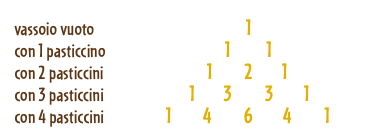
Lasciamo al lettore il compito di scrivere altre righe del Triangolo di Tartaglia: oltre all’1 iniziale e finale, ogni termine è la somma dei due numeri che si trovano nella riga precedente, uno alla sua sinistra e l’altro alla sua destra.

Ebbene, eccoci pronti a comprendere il modello pasticcini a volontà: se non vogliamo stabilire quanti pasticcini prendere dal vassoio, ma ci lasciamo liberi di servirci senza limiti, in quanti modi possiamo servirci? Facile: basterà fare le somme dei termini di ogni riga.Eccole pronte:

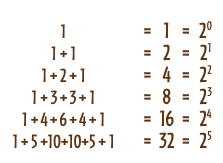
Dunque, in generale, potremmo riassumere così: dato un insieme di n elementi sono \(2^n\) tutti i suoi possibili sottoinsiemi. Questo risultato non ci stupisce perché è inquadrabile nel modello quante parole. Infatti, per ogni elemento dell’insieme basterà scrivere 0 se non è nel sottoinsieme e 1 se c’è: quindi ogni sottoinsieme corrisponderà a una parola lunga n scritta con l’alfabeto \(\{0,1\}\).
Restando in tema di dolci, dal triangolo di Tartaglia possiamo anche conoscere i brindisi che i vari insiemi di persone possono fare: si tratta del terzo numero di ogni riga che, infatti, dice il numero di sottoinsiemi da 2 elementi.

Per concludere ecco pronti due quiz a partire da queste 4 figure

• quanti diversi braccialetti con due di esse posso costruire oltre i due che seguono?

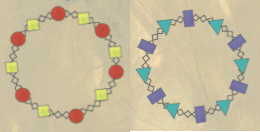
• e, sempre usandone solo 2, quanti diversi segnaposto oltre ai quattro che seguono, si possono disegnare con la stessa struttura?

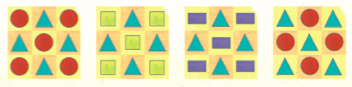
Per ora ci fermiamo qui. Buon divertimento con il Calcolo Combinatorio!

3-fine

Anna Cerasoli

Tutte le puntate le ritrovate raccolte in questa pagina.       

BIBLIOGRAFIA

• Anna Cerasoli. Sono il numero 1. Come mi sono divertito a diventare bravo in matematica!  con Ilaria Faccioli (Illustratrice), Feltrinelli, 2008, Collana: Feltrinelli Kids,129 p., ill. , Brossura, EAN:  9788807921278.

• Anna Cerasoli. La sorpresa dei numeri. Un viaggio nella matematica simpatica,  con A. Gon (Illustratore), Editoriale Scienza, 2013, Collana: Non solo numeri. Pagine: 176 p., ill. , Rilegato, EAN: 9788873076209.

• Anna Cerasoli. Matematica amica. Ediz. illustrata, con Gaia Stella (Illustratrice), Feltrinelli, 2016. Collana: Feltrinelli Kids. Saggistica narrata. 124 p., ill. , Brossura. Età di lettura: Da 8 anni. EAN: 9788807922787

• Anna Cerasoli e Giuseppe Vitale, Quattro artisti che contano.  Artebambini, 2018. 40 p., ill. , Rilegato. Da 3 anni. EAN: 9788898645589

Crediti delle immagini. Se non indicato le immagini sono di proprietà dell’autrice.