Quest’anno ricade il 50-esimo anniversario della \(\Gamma\)-convergenza, una nozione di convergenza introdotta da Ennio de Giorgi nel 1975 e molto utilizzata nel Calcolo della Variazioni. Insieme a Riccardo Moraschi ripercorriamo la sua storia e proveremo a comprenderne il significato in modo intuitivo.
Per il 50-esimo anniversario della \(\Gamma\)-convergenza è doveroso iniziare ricordando la figura di De Giorgi. Ennio De Giorgi (1928-1996) è stato uno dei matematici italiani più brillanti e originali del Novecento. Nato a Lecce e vissuto a lungo a Pisa, ha rivoluzionato il modo in cui si affrontano molti problemi di analisi, introducendo idee nuove come la \(\Gamma\)-convergenza, oggi indispensabile in molti campi della matematica. De Giorgi non era solo uno scienziato di straordinario talento: era anche un pensatore curioso, aperto al dialogo con la filosofia, la teologia e persino con i problemi sociali, convinto che la matematica non fosse una torre d’avorio ma un ponte verso il mondo.
La teoria della \(\Gamma\)-convergenza è stata sviluppata a partire da un esempio semplice e pragmatico che De Giorgi discuteva già a metà degli anni Sessanta. Nell’articolo “Su un tipo di convergenza variazionale” [1 ] E. De Giorgi e T. Franzoni. “Su un tipo di convergenza variazionale”. In: Atti della Accademia Nazionale dei Lincei. Classe di Scienze Fisiche, Matematiche e Naturali. Rendiconti 58.6 (1975), pp. 842–850. del 1975, De Giorgi decide di superare l’approccio della G-convergenza elaborato in precedenza con Sergio Spagnolo, orientandosi verso una formulazione esclusivamente variazionale. La \(\Gamma\)-convergenza svela un tesoro ricco di nuovi problemi, alcuni dei quali sono stati proposti da De Giorgi fin dall’inizio, come stabilire se alcune famiglie di funzionali siano \(\Gamma\)-compatte, o almeno \(\Gamma\)-chiuse. Lo stesso De Giorgi, che di solito era modesto quando parlava dei suoi risultati, era molto orgoglioso di questa creazione, e la considerava uno strumento concettuale con grandi potenzialità.
Leggi l’articolo di De Giorgi e Franzoni conservato nella BDIM
Per capire la \(\Gamma\)-convergenza richiamiamo rapidamente il metodo diretto, una tecnica molto utilizzata nel Calcolo delle Variazioni.
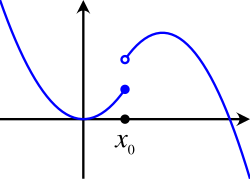
Esempio di funzione semicontinua inferiormente

Esempio di funzione non semicontinua inferiormente
Ora che abbiamo una tecnica per mostrare l’esistenza di un minimo, è interessante domandarsi cosa succede quando abbiamo una successione di minimi: consideriamo una successione di funzionali \(F_n\) e ci domandiamo se riusciamo a trovare un funzionale \(F\) tale che
\[ \inf \left\{F_n(u): u \in X\right\}\to \inf \left\{F(u): u \in X\right\}.\] Quindi quello che vogliamo fare è definire una convergenza di funzionali che riesca a garantirci che i minimi tendano ai minimi: la difficoltà è che per i funzionali esistono molti tipi di convergenza diverse tra loro (puntuale, uniforme, in misura ecc) e capire quale sia quella adatta, se ne esiste una, è molto complicato.
Per intuire come deve essere strutturata questa convergenza, ispirati da quanto detto sul metodo diretto, una strada potrebbe essere generalizzare la nozione di coercività e semicontinuità inferiore. Riguardo alla prima non ci sono particolari problemi (sarà sufficiente prendere i funzionali \(F_n\) coercivi “allo stesso modo”), mentre riguardo alla semicontinuità c’è più lavoro da fare. Ennio De Giorgi ha capito quali erano le condizioni necessarie, definendo così la nozione di \(\Gamma\)-convergenza. Più precisamente dato \((X,d)\) uno spazio metrico, \(F_n: X \to \overline{\mathbb{R}}\) una successione di funzionali, \(u \in X\) e \(F: X \to \overline{\mathbb{R}}\) una funzione, diremo che \(F_n\) \(\Gamma\)-converge a \(F\) in \(u\) se sono verificate le seguenti disuguaglianze:
- liminf inequality: per ogni successione \((u_n)\) convergente a \(u\) vale \[ \liminf_n F_n(u_n)\geq F(u). \]
- limsup inequality: esiste una successione \((u_n)\) convergente a \(u\) tale che \[ \limsup_n F_n(u_n)\leq F(u). \]
Osserviamo che le condizioni sopraindicate ricordano in un certo modo le definizioni di semicontinuità inferiore e superiore, ma con la differenza che nel limite i funzionali variano e non sono fissi. Similmente a quanto detto con il metodo diretto, sfruttando la nozione di \(\Gamma\)-convergenza e assumendo ipotesi analoghe alla coercività, vale il seguente teorema:
- [leggera equi-coercività] esiste un insieme compatto e non vuoto \(K\subset X\) tale che \(\inf_K F_n=\inf_X F_n \) per ogni \(n\).
- [\(\Gamma\)-convergenza] \(F_n\) \(\Gamma\)-converge a \(F\).
Allora \(F\) ammette minimo e \[ \lim_{n} \inf_{u\in X} F_n(u)=\min_{u\in X} F (u). \] Inoltre se \((u_n)\) è una successione di quasi minimi, cioè \[ \lim_n \left(F_n(u_n)- \inf_{X} F_n\right)=0,\] e ammette sottosuccessione convergente a \(\tilde u\), allora \[\tilde u\in \text{argmin}\left\{F(u):u \in X\right\}.\]
Riassumendo, quando si ha una successione di funzionali, la \(\Gamma\)-convergenza ci permette di capire qual è il funzionale per cui un suo minimo è limite dei minimi dei funzionali nella successione: l’obbiettivo è studiare qual è il \(\Gamma\)-limite. Viceversa, la \(\Gamma\)-convergenza può anche essere usata per studiare il minimo di un funzionale appoggiandoci ai minimi di funzionali ausiliari, più semplici da analizzare.
Per concludere facciamo un esempio. Consideriamo un insieme aperto limitato \(\Omega\subseteq \mathbb{R}^n\) e perforiamolo con dei buchi sferici: \[ \Omega_\varepsilon=\Omega\setminus \bigcup_{i\in \mathbb{Z}^n} B(\varepsilon i, \delta(\varepsilon)), \]dove \(\delta(\varepsilon)=\varepsilon^{n/(n-2)}\).

Cosa succede al problema \[ \inf\left\{ \int_{\Omega_\varepsilon} |\nabla u|^2dx: u\in H^1_0(\Omega_\varepsilon) \right\}\] quando \( \varepsilon\to 0\)? (Per chi non conoscesse lo spazio \(H^1_0(\Omega_\varepsilon) \) pensi a delle funzioni \(C^1(\Omega_\varepsilon)\) tali che \(u=0\) su \(\partial\Omega_\varepsilon\). In realtà qui non si chiede che le derivate siano continue, basta che le derivate (deboli) siano limitate in \(L^2(\Omega)\)) Verrebbe da pensare che questi minimi convergano al minimo dello stesso problema con \(\Omega\) anzichè \(\Omega_\varepsilon\) ma quello che accade è ben diverso. Infatti studiando il \(\Gamma\)-limite di questo funzionale si può osservare che converge al problema \[ \inf\left\{ \int_{\Omega} (|\nabla u|^2+C|u|^2)dx : u\in H^1_0(\Omega) \right\}\], ossia appare un termine supplementare che tiene conto dell’accumularsi dei buchi. In altre parole, la \(\Gamma\)-convergenza ci ha permesso di capire qual è il problema limite a cui tendono i minimi presi in considerazione. Questo esempio mostra come la \(\Gamma\)-convergenza sia uno strumento molto forte, in grado di risolvere problemi di notevole complessità.
Ringraziamo De Giorgi per questa meravigliosa idea!
Crediti: le foto sono prese da Wikipedia e [2 ] A. Braides, “\(\Gamma\)-convergence for Beginners”. New York : Oxford University Press, 2002. .
Note e riferimenti
| ⇧1 | E. De Giorgi e T. Franzoni. “Su un tipo di convergenza variazionale”. In: Atti della Accademia Nazionale dei Lincei. Classe di Scienze Fisiche, Matematiche e Naturali. Rendiconti 58.6 (1975), pp. 842–850. |
|---|---|
| ⇧2 | A. Braides, “\(\Gamma\)-convergence for Beginners”. New York : Oxford University Press, 2002. |



















Anche se per le mie conoscenze limitate quasi sconosciute a questi livelli è semplicemente stupendo tuffarsi in questa matematica da un appassionato di matematica con livello studi delle superiori.