Una nuova mini-serie, fatta di video e articoli, di Alessandro Zaccagnini, matematico, esperto di teoria dei numeri, autore del Dialogo sui numeri primi. Questa volta si fa accompagnare da una tartaruga per raccontarci cosa sono le somme esponenziali e perché sono tanto utili nella sua disciplina. Questa è la seconda puntata. Tutte le puntate le trovate su questa pagina.

Un po’ di calcoli

Pentagono regolare e pentagono intrecciatoLe figure viste nella prima puntata sembrano indicare che se ruotiamo il vettore di partenza di \((360 / n)^\circ\) e sommiamo i vettori ottenuti via via, dopo esattamente \(n\) passi torniamo all’origine, dopo aver descritto un \(n\)-agono regolare, per ogni intero \(n \ge 3\). È veramente cosí? E se sí, perché? Se proviamo a fare il contrario, cioè partiamo dal poligono regolare e otteniamo i corrispondenti vettori unitari, è chiaro che questi formano angoli costanti fra ciascuno e il successivo.

Per giustificare questa scoperta empirica e dimostrarla in generale abbiamo bisogno di utilizzare i numeri complessi. In particolare, ci serve ricordare le forma esponenziale dei numeri complessi e la proprietà che moltiplicare corrisponde a sommare la fase. Se \(z_1\) e \(z_2\) sono numeri complessi, esistono numeri reali \(\rho_1 \ge 0\) e \(\rho_2 \ge 0\), e \(\theta_1\), \(\theta_2 \in [0, 2 \pi)\) tali che \[z_1 = \rho_1 \mathrm{e}^{\mathrm{i}\theta_1}
\qquad\text{e}\qquad
z_2 = \rho_2 \mathrm{e}^{\mathrm{i}\theta_2}
\qquad\text{e dunque}\qquad
z_1 z_2 = \rho_1 \rho_2 \mathrm{e}^{\mathrm{i}(\theta_1 + \theta_2)}.\] Tutti i nostri vettori sono unitari, cioè hanno \(\rho = 1\) e quindi ci dobbiamo preoccupare solo delle fasi, cioè dei numeri \(\theta\), che rappresentano gli angoli di cui stiamo parlando.

Per \(n \ge 3\) poniamo \(\alpha_n = 2 \pi / n\); dunque \(\alpha_n\) è un \(n\)-esimo di un angolo giro, misurato in radianti. La rotazione di \(\alpha_n\) corrisponde alla moltiplicazione per \(q = q_n = \mathrm{e}^{\mathrm{i}\alpha_n}\). I vettori che consideriamo sono dunque \[1, q, q^2, q^3 , \dots, q^{n – 1}.\] Questi numeri complessi sono detti radici \(n\)-esime dell’unità, perché sono tutte e solo le soluzioni complesse dell’equazione \(z^n = 1\); sono i punti che si trovano in corrispondenza delle punte delle frecce rosse nelle figure della prima puntata.

Per calcolare il valore di \(S(q) = 1 + q + q^2 + \dots + q^{n – 1}\) abbiamo bisogno di ricordare la formula per la somma dei primi termini di una progressione geometrica: se \(x\) è un qualunque numero complesso diverso da 1 ed \(m \ge 0\) è intero, allora \[%\label{sum-prog}
1 + x + x^2 + \dots + x^m
=
\frac{1 – x^{m + 1}}{1 – x}.\] La dimostrazione di questa formula, che era certamente nota agli antichi Greci, si ottiene facilmente per induzione. Nel caso che ci interessa abbiamo \(x = q\) ed \(m = n – 1\): sostituendo nella formula qui sopra e ricordando che \(q^n = 1\) troviamo che effettivamente \(S(q) = 0\). In alternativa, \(S(q) = 1 + q + q^2 + \dots + q^{n – 1} = q^n + q +
q^2 + \dots + q^{n – 1} = q + q^2 + \dots + q^{n – 1} + q^n = q S(q)\), cioè \((q – 1) S(q) = 0\); poiché \(q \ne 1\) concludiamo che \(S(q) = 0\). In effetti, \(q S(q)\) non è altro che la somma degli stessi vettori cominciando dal secondo e finendo con il primo.

La successione \(1, q, q^2, q^3, \dots\), prolungata oltre i primi \(n\) valori, è periodica di periodo \(n\), proprio perché \(q^n = 1\), e quindi si ripete da capo. Dunque, se invece di sommare \(n\) termini consecutivi ne sommiamo \(2 n\), o \(3 n\) o un qualunque multiplo di \(n\) troviamo 0: la tartaruga ritorna esattamente sui suoi passi e ripete lo stesso percorso in eterno. Questo dipende dal fatto che l’angolo di cui ruotiamo è un sottomultiplo di un angolo giro; lo stesso succede, piú in generale, se l’angolo è in rapporto razionale con l’angolo giro. Questo è il caso illustrato nella prossima figura, nella quale abbiamo un poligono “intrecciato.”

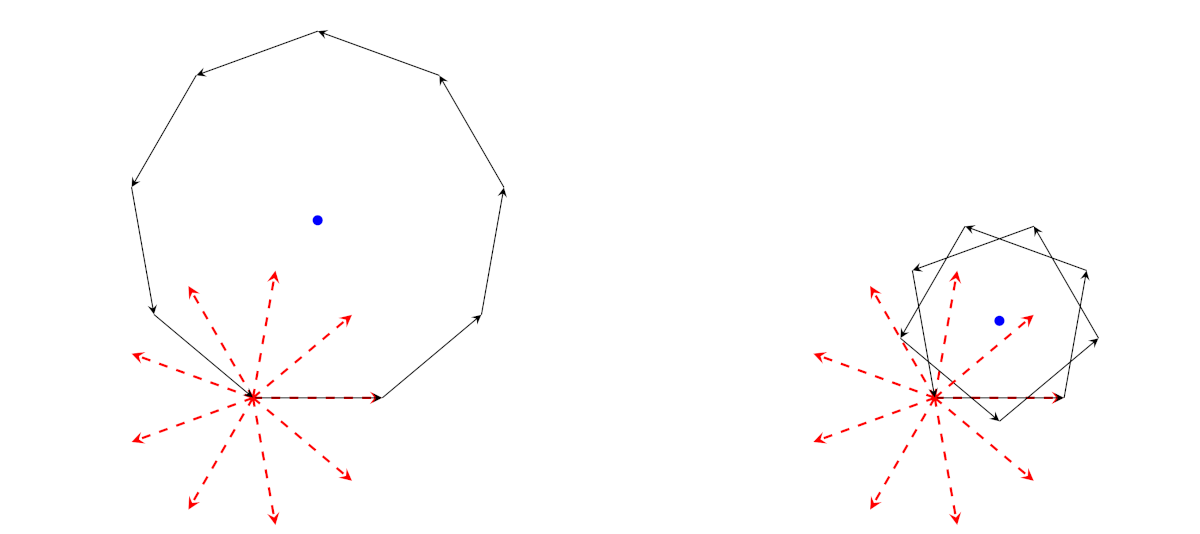
A sinistra il caso \(n = 9\); a destra prendiamo gli stessi vettori in un altro ordine. Invece di ruotare di \(40^\circ = (360 / 9)^\circ\) ruotiamo di \(80^\circ\). La somma di tutti i vettori, evidentemente, ha lo stesso valori di prima e cioè 0, ma invece di ottenere il poligono regolare otteniamo un poligono intrecciato.

to poligono :lunghezza :angolo :iterazioni
  clearscreen
  showturtle
  setheading 90
  pendown
  setcolor pick [red]
  repeat :iterazioni [
    fd :lunghezza
    setxy 0 0
    rt -:angolo
    wait 10]
  penup
  home
  pendown
  setheading 90
  setcolor pick [black]
  repeat :iterazioni [
    fd :lunghezza
    rt -:angolo
    wait 10]
end

Una funzione in logo per generare una sequenza di :iterazioni vettori di lunghezza :lunghezza, ciascuno ruotato di :angolo gradi in direzione antioraria rispetto al precedente, ed il “poligono” associato. Qui l’angolo di rotazione è specificato esplicitamente e non calcolato a partire dagli altri dati: il “poligono” che si ottiene potrebbe non chiudersi, come negli esempi che seguiranno, e quindi è necessario indicare il numero di iterazioni desiderate. L’istruzione poligono 200 80 9 richiama la funzione e disegna il poligono intrecciato della figura precedente.