Una nuova mini-serie, fatta di video e articoli, di Alessandro Zaccagnini, matematico, esperto di teoria dei numeri, autore della fortunata serie “Dialogo sui numeri primi“, questa volta per raccontarci tante diverse dimostrazioni di un unico Teorema: 

Teorema (Euclide). Esistono infiniti numeri primi.

Questa è la prima puntata (trovi la presentazionedella serie qui).

La dimostrazione di Euclide

Sia $\mathcal{P}= \{ p_1$, $p_2$, …, $p_k \}$ un insieme finito di numeri primi. Il numero $N = p_1 \cdot p_2 \cdots p_k + 1$ non è divisibile per nessuno dei numeri primi in $\mathcal{P}$, perché la divisione dà resto $1$. $N$ è primo, o prodotto di numeri primi non appartenenti a $\mathcal{P}$. In ogni caso, $\mathcal{P}$ non è l’insieme di tutti i numeri primi.

Vediamo due esempi di quello che può accadere. Se $\mathcal{P}= \{2$, $3$, $5 \}$, allora $N = 2 \cdot 3 \cdot 5 + 1 = 31$ è primo. Se $\mathcal{P}= \{2$, $5$, $11 \}$: allora $N = 2 \cdot 5 \cdot 11 + 1 = 111 = 3 \cdot 37$ non è primo. In entrambi i casi abbiamo trovato almeno un numero primo non appartenente a $\mathcal{P}$.

Una formulazione equivalente

I Matematici greci preferivano non parlare di insiemi infiniti. Possiamo usare l’idea esposta sopra per enunciare e dimostrare una variante.

L’insieme dei numeri primi è illimitato superiormente.

Sia $n$ un qualsiasi intero positivo e sia $p$ un qualsiasi fattore primo di $M = n! + 1$: evidentemente $p > n$ dato che $M \equiv 1 \bmod m$ per ogni intero $m \in [2, n]$. Dunque l’insieme dei numeri primi è illimitato superiormente.

In questa tabella $p_n$ indica il piú piccolo fattore primo di $n! + 1$. 
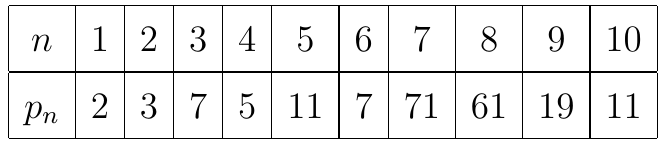Oltre a verificare la correttezza della dimostrazione qui sopra, questa tabella ci permette di “indovinare” il Teorema di Wilson: se $p$ è un numero primo (2, 3, 5, 7, 11, nel nostro caso) allora $(p – 1)! + 1$ è divisibile per $p$.

La figura illustra cosa vuol dire in concreto dimostrare che l’insieme dei numeri primi è illimitato: scelto comunque l’intero $n$, possiamo determinare un numero primo $p_n > n$, e quindi $n$ non è una limitazione superiore per l’insieme dei numeri primi.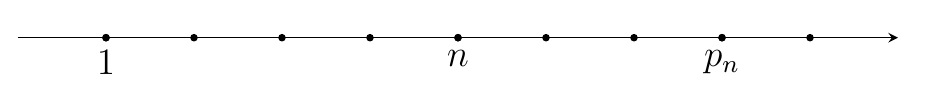

Qualche osservazione per concludere: per $n \ge 3$, anche i fattori primi di $M = n! – 1$ sono tutti $> n$, perché dividendo $M$ per un qualunque intero $m \in [2, n]$ troviamo il resto $m – 1$. Possiamo dunque usare le idee esposte per dimostrare anche altri risultati simili al Teorema di Euclide.

1. Osserviamo che $n! – 1 \equiv 3 \bmod 4$ per $n \ge 4$. Quindi esistono infiniti numeri primi nella progressione $3$ modulo $4$: per esempio $5! – 1 = 120 – 1 = 7 \cdot 17$ e $7 \equiv 3 \bmod 4$. Infatti, se tutti i numeri primi da un certo punto in poi appartenessero alla classe $1$ modulo $4$, allora per $n$ abbastanza grande anche $n! – 1$ dovrebbe avere tutti i suoi fattori primi in questa classe di resto, e quindi $n! – 1$ sarebbe $\equiv 1 \bmod 4$.
2. Analogamente, $n! – 1 \equiv 5 \bmod 6$ per $n \ge 3$. Quindi esistono infiniti numeri primi nella progressione $5$ modulo $6$: per esempio $6! – 1 = 720 – 1$ è primo ed è $\equiv 5 \bmod 6$.
3. I campi finiti non sono algebricamente chiusi: basta considerare il prodotto di tutti i polinomi monici di primo grado e aggiungere $1$. Per esempio, se prendiamo il campo con 5 elementi, il polinomio $p(x) = x (x – 1) (x – 2) (x – 3) (x – 4) + 1$ non ha radici poiché $p(a) = 1$ per ogni elemento $a$ del campo stesso. In realtà, questo fatto è collegato al Piccolo Teorema di Fermat, perché anche il polinomio $q(x) = x^5 – x + 1$ ha la stessa proprietà e infatti $p(x) \equiv q(x) \bmod 5$.

Alessandro Zaccagnini