Nei giorni scorsi è stato annunciato che Roger Penrose è uno dei tre vincitori del premio Nobel per la fisica 2020. Raccogliamo qui una serie di ricordi di Michele Emmer, che ha conosciuto Penrose e con cui ha collaborato in passato.
Era ora! È il caso di dirlo. Finalmente a Sir Roger Penrose, alla soglia dei 90 anni (è nato il 8 agosto 1931) viene assegnato il premio Nobel per la fisica per le sue ricerche sui buchi neri dell’universo, iniziate molto decenni fa. Ha lavorato per molti anni con Stephen Hawking, morto due anni fa. Nel film sulla vita di Hawking, The Theory of Everything [1 ]J. Marsh, regia, The theory of Everything, con E. Redmayne, F. Jones, E. Watson, soggetto di Jane Wolde Hawking, sceneggiatura di Anthony McCarten, 123’, Working Title Films, UK-Giappone-USA (2014), per il quale Eddie Redmayne ha ricevuto l’Oscar come migliore attore, compariva brevemente anche Roger Penrose, impersonato dall’attore Christian McKay. Non scriverò di buchi neri, ma di due altri interessi che Penrose ha avuto nella sua vita, tra i tanti: Escher e i quasi cristalli. Penrose è sempre stato una persona piena di interessi e creativa, ma anche gentile, disponibile, che mi ha affascinato sin da subito, e così i mei studenti di fisica che hanno passato con lui dei giorni indimenticabili durante il convegno su Escher a Roma nel 1985.
M. C. Escher e Penrose
L’incontro tra Penrose ed Escher era inevitabile. Avviene al congresso mondiale di matematica di Amsterdam nel 1954, Penrose è uno studente di matematica. Al convegno era presentata la prima mostra importante dedicata al grafico olandese. Nel film Escher: Geometries and Impossible Worlds [2 ]M. Emmer, regia, Escher: Geometries and Impossible Worlds, seconda parte del film The Fantastic World of M. C. Escher, serie Art and Mathematics, con D. Coxeter, R. Penrose, C. Macgillavry, B. Ernst, sceneggiatura M. Emmer, 50’, prod. M. Emmer, 2000 che abbiamo girato a Roma, così racconta:
“Mi fu detto che le stampe e i disegni di Escher avrebbero interessato particolarmente i matematici. Si sapeva che mi interessavo di curiosità matematiche, in particolare di quelle geometriche. In effetti quando andai a vederla la trovai particolarmente affascinante. Quando tornai in Inghilterra cominciai a pensare se sarei stato capace di fare anch’io qualcosa di geometricamente bizzarro, ma non proprio dello stesso genere delle cose che avevo visto alla mostra di Escher. Quindi ho cominciato a fare dei disegni che erano in un certo senso impossibili. Li ho via via semplificati finché ho disegnato il triangolo, che è un tipo di cosa, come potrei dire, un oggetto impossibile [oggi è noto come triangolo di Penrose]. Qual è l’idea? È che nel triangolo ogni parte della figura potrebbe esistere come oggetto tridimensionale, ma tutta la configurazione è un qualcosa che non potrebbe esistere nello spazio. Mostrai il disegno a mio padre Lionel (psichiatra e genetista) e lui disegnò un certo numero di figure impossibili e arrivò a disegnare le scale che scendono sempre in un modo impossibile. Qualche tempo dopo inviammo un articolo che conteneva un certo numero di disegni al British Journal of Psychology [3 ]L. S. Penrose e R. Penrose, Impossible Objects: A Special Type of Visual Illusion, vol. 49, n. 1, p 31-33 (1958), il triangolo e le scale dei Penrose sono divenuti un classico non solo in teoria della percezione visiva ma anche in psicologia]. Quando vennero pubblicati ne inviammo una copia a Escher, ed egli incorporò i disegni in alcune delle sue opere.

Triangolo e scala di Penrose
Roger Penrose ha poi ribadito nel suo lavoro Escher and the Visual Representation of Mathematical Ideas [4 ]R.Penrose, Escher and the Visual Representation of Mathematical Ideas, in H.S. M. Coxeter, M. Emmer, R. Penrose, M.L. Teuber, eds M.C. Escher: Art and Science, North-Holland, Elsevier Publ., Amsterdam (1986), p. 143-158 che Escher aveva creato nello stesso periodo ma in modo del tutto indipendente la sua incisione Belvedere. Nella sezione del suo primo libro, dedicata agli oggetti impossibili, Escher ricorda come siano stati i disegni dei Penrose a ispirare le sue opere Ascending and descending e Waterfall [5 ]M.C. Escher, The Graphic Work, MacDonald & C. Publ., London (1961). (Vale la pena ricordare che né i Penrose né Escher sono stati i primi a utilizzare graficamente gli oggetti impossibili, in particolare il triangolo. A parte le situazioni dovute a errori più o meno consapevoli da parte di artisti, sembra che il primo sia stato l’artista svedese Oscar Reutersvärd sin dal 1934. Sia Escher che i Penrose lo ignoravano.)

M. C. Escher, Belvedere, litografia 1958
Avevo conosciuto Penrose quando stavo realizzando il film su Escher. Se non ricordo male era stato il matematico inglese, trasferitosi a Toronto, Harold Scott MacDonald (Donald) Coxeter che mi inviò i suoi recapiti. Anche Coxeter partecipava al film. Penrose accettò di venire a Roma per le riprese. Penso che fosse il 1980 o il 1981. Per semplicità i suoi due interventi, uno per il film su Escher di circa 13 minuti e quello sulle simmetrie aperiodiche di circa 5 minuti vennero realizzati il primo nel salotto e il secondo nello studio libreria a casa mia. Penrose aveva portato con sé i modelli originali del triangolo e delle scale. Il film fu girato in pellicola 16 mm con il sonoro in presa diretta. A parte vennero filmati i dettagli dei due oggetti e poi inseriti in fase di montaggio.

M. C. Escher, Waterfall, litografia, 1961
Penrose e i quasicristalli
Una delle cose che interessavano molto Escher erano le simmetrie dei ricoprimenti piani, quelle che si chiamano tassellazioni. Un motivo che riempie tutto il piano in modo simmetrico e ripetitivo all’infinito. I pesci, gli uccelli, tanti sono i disegni periodici inventati da Escher. Solo dopo la sua morte nel 1972 furono trovati da un collezionista, che aveva acquistato il materiale lasciato dall’artista, i taccuini di Escher con più di un centinaio di acquarelli e disegni periodici. Tutto materiale di cui il Gemeentemuseum dell’Aia si disfece. I disegni ed acquarelli dei notebooks vennero venduti separatamente dal collezionista, ma fortunatamente prima della loro distruzione fu permesso a Doris Schattschneider di farli riprodurre insieme a molti altri disegni preparatori nel libro M. C. Escher: Vision of Symmetry [6 ]D. Schattshneider, M. C. Escher: Vision of Symmetry, Freeman, New York, 1990.. Simmetrie presenti in molte opere del grafico olandese che si chiamano cristallografiche perché sono tipiche dei cristalli. Queste simmetrie sono per loro natura periodiche. Per esempio non possono esistere simmetrie periodiche con struttura pentagonale: con delle mattonelle pentagonali non si può riempire il piano, resterebbero dei vuoti. Insomma, cristalli con simmetria pentagonale non possono esistere.
Questa certezza viene messa in discussione nel 1984 in uno degli esempi più interessanti di come la matematica sia irragionevolmente legata alla realtà fisica e in tutto questo c’entra ancora Penrose. Nel novembre 1984 viene pubblicato un lavoro intitolato Metallic Phase with Long-Range Orientational Order and no Translational Symmetry, autori i fisici Dany Schechtman, Ilan Blech, Denis Gratias e John Cahn [7 ]D. Shechtman, I. Blech, D. Gratias, and J. W. Cahn. Metallic Phase with Long-Range Orientational Order and No Translational Symmetry, Phys. Rev. Lett., 53, 195, 12 November 1984. La pubblicazione di questo lavoro ha dato origine a un vastissimo dibattito tra i matematici, i fisici, i cristallografi e i chimici. Metteva in crisi una delle basi della cristallografia. Nei cristalli la presenza di un ordine a lungo raggio è sinonimo di periodicità, e ogni struttura periodica ha una cella che ripetuta all’infinito costruisce tutta la struttura. Ecco allora che, già nel titolo il lavoro pubblicato nel 1984 contraddiceva le idee alla base della cristallografia: ordine a lungo raggio e assenza di simmetria traslatoria, due proprietà che sembravano in netto contrasto tra loro. In questa sorta di quasicristalli, osservati con tecniche di microscopia elettronica o di diffrazione, si osservava una sistemazione su larga scala della simmetria di tipo pentagonale, e non vi era alcuna cella che ripetuta all’infinito generasse tutta la struttura. Si era verificato l’impossibile, come hanno scritto Marjorie Senechal e Jean Taylor. La Taylor dimostrò tra l’altro nel 1976 in un famoso articolo che le regole che il fisico Joseph Plateau aveva indicato per gli angoli delle lamine saponate erano corrette.
Dal 1984 gli scienziati hanno cercato di modificare i loro modelli per tener conto delle nuove esperienze. Bisogna dire che Schechtman fu trattato malissimo, gli vennero tolti i fondi di ricerca, fu attaccato in malo modo. Era già molto tempo che si discuteva, in linea teorica, se potesse esistere una nuova area della cristallografia in cui fosse possibile avere la simmetria pentagonale e le altre non ammissibili. Questa domanda veniva posta spesso, tra la fine degli anni settanta e l’inizio degli anni ottanta, a Roger Penrose, che aveva scoperto in quegli anni un certo numero di ricoprimenti del piano che avevano le due proprietà di avere simmetrie non ammesse nella cristallografia classica e di non essere di tipo periodico, nel senso che vi erano chiaramente regioni simmetriche che si ritrovavano nella struttura in scale diverse senza tuttavia una periodicità globale. I ricoprimenti di Penrose erano quasiperiodici. Il nome quasicristalli deriva dalla contrazione di cristalli quasiperiodici. Quando gli veniva chiesto se i suoi risultati potessero essere la premessa per un’area del tutto nuova della cristallografia, di solito Penrose rispondeva: “In linea di principio, sì; ma come potrebbe la natura operare in questo modo?”.
Di alcuni di questi ricoprimenti Penrose fece anche una versione per bambini; modificò le due figure geometriche che servivano a generare uno dei ricoprimenti, chiamati per la loro forma dard e kite, in due tipi di uccelli; purtroppo, a parte alcuni prototipi, la versione giocattolo del ricoprimento trovata da Penrose non venne mai costruita su larga scala: era ritenuta troppo complicata. Nel film Symmetry and tassellation [8 ]M. Emmer, regia, Symmetry and tessellations, serie Art and Mathematics, con R. Penrose, R. Vlad, M. Wurtz, sceneggiatura M. Emmer, 25’, prod. M. Emmer, 1980, sempre girato a Roma, Penrose illustrava il suo mosaico-puzzle con i due tipi di uccelli; la sequenza terminava con la composizione in animazione del puzzle.
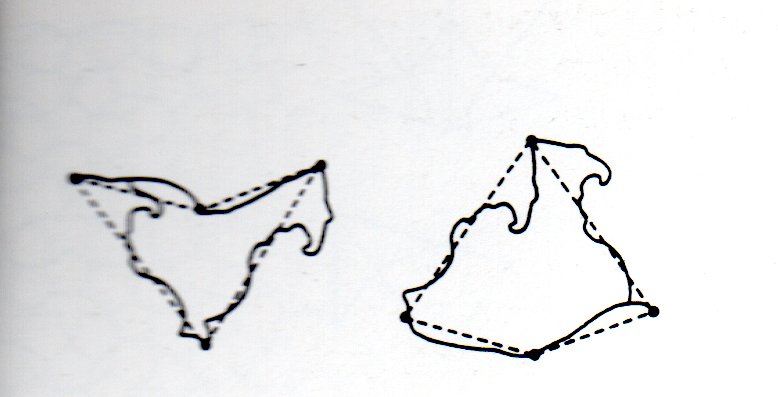
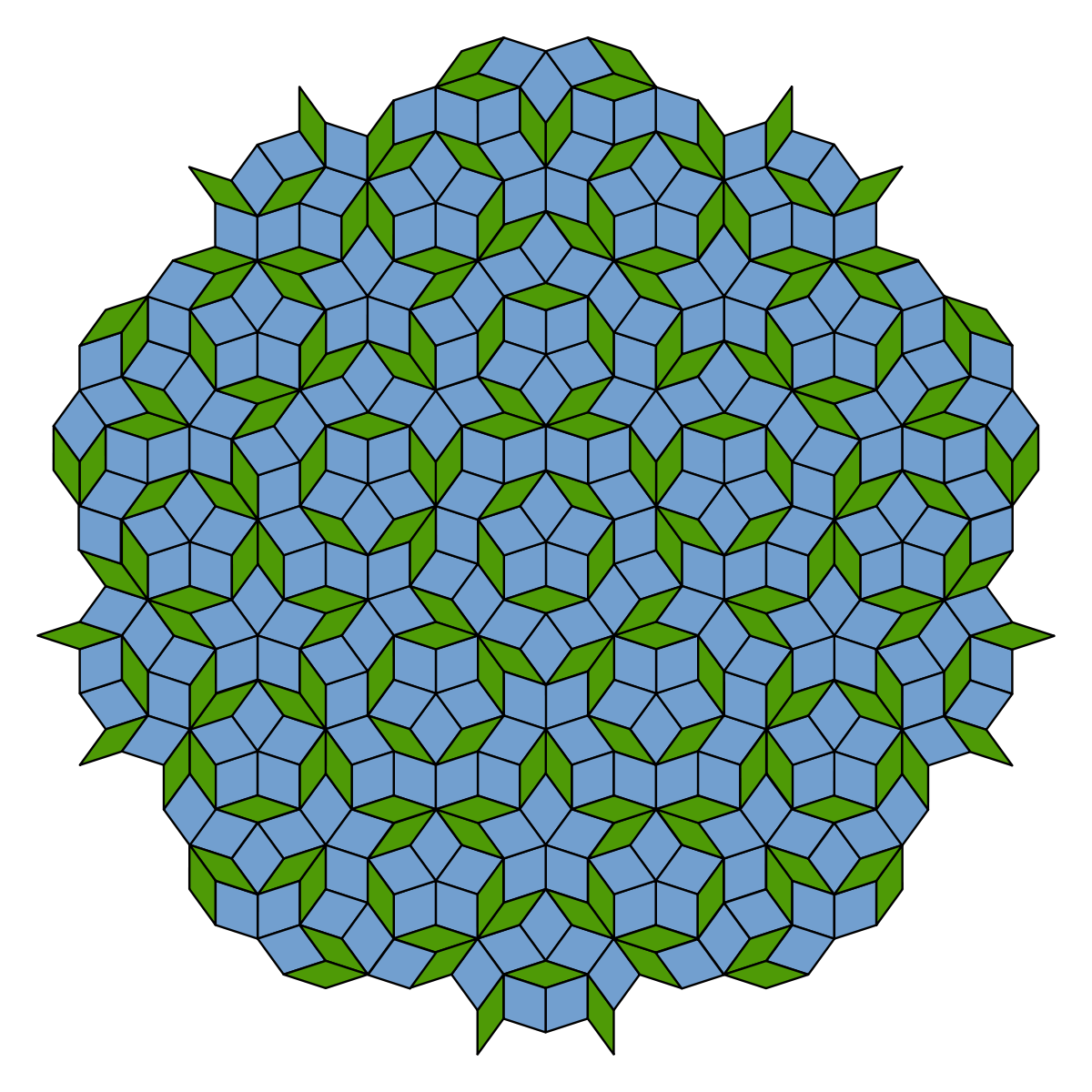
Ricoprimenti di Penrose
Penrose era in piedi davanti un tavolo e dopo aver montato un paio di mosaici periodici di Escher faceva vedere i due tipi di uccelli che servivano alla realizzazione della tassellazione che aveva inventato. Alla fine poggiava i due uccelli sul tavolo e la ripresa si interrompeva. Quindi tutti i pezzi del mosaico sono stati portati in un laboratorio di animazione per realizzare il filmato a passo uno, cioè a dire ogni fotogramma è una fotografia separata dell’immagine che si vuole animare e le migliaia di fotografie che si ottengono vengono poi montate insieme per vedere l’animazione completa. È un lavoro di grande pazienza. In realtà per il film su Escher si fecero 4 foto di ogni fotogramma per avere un movimento più fluido e lineare, altrimenti sarebbe stato troppo veloce e incomprensibile. Per le riprese si usò una macchina da presa speciale che si chiamava truka verticale. Parallela al piano delle riprese e fissata solidamente per tutte le riprese, fotografava le diverse posizioni dell’animazione. Il cameramen scattò tante copie della stessa posa, in questo caso quattro. Ovviamente le animazioni si fanno al contrario. Si parte dalla fine, con l’immagine che sarà quella finale, quando le riprese saranno riversate al contrario per la proiezione. Penrose compose la sua tassellazione, operazione non facile da fare dato che non è globalmente periodica. Ma il trucco c’era. Dall’altra parte dei singoli pezzi del mosaico erano tracciate delle linee che permettevano facilmente di ricomporre la tassellazione che era grande un metro per un metro e composta da centinaia di piccoli pezzi. Poi con pazienza si toglieva un pezzo alla volta, lo si fotografava 4 volte e si continuava. Bisognava fare estrema attenzione perché se un pezzo si muoveva anche di un millimetro nel film si sarebbe visto un saltino. All’epoca avevo imparato a fare tutte queste operazioni, soprattutto per realizzare il film tutto in animazione Flatland tratto dal racconto di Edwin Abbott, con le musiche originali di Ennio Moricone [9 ]M. Emmer, regia, Flatland, animazione, scenografia, sceneggiatura M. Emmer, 24’, prod. M. Emmer 2000; M. Emmer, ed., introduzione e postfazione, Flatlandia di E. A. Abbott con testo a fronte, con DVD del film (2008), senza DVD (2019), Bollati Boringhieri, Torino. Alla fine del lavoro, durato quattro giorni tra le riprese in casa, le animazioni in studio, la stampa della pellicola, la visione del girato, il montaggio alla moviola, la scena durava compresa l’animazione non più di due minuti. Ma il risultato fu molto buono. Ovviamente non ero solo, c’erano il cameraman, il fonico, il tecnico delle luci, il tecnico della truka e Penrose.

Fotogrammi dal film Symmetry and Tessellations
Tornando ai quasicristalli la cosa irragionevole è che se si ricostruisce con un computer la figura di diffrazione generata dalla distribuzione di punti ai vertici dei rombi di un ricoprimento di Penrose, si ottiene la stessa simmetria delle immagini di diffrazione ottenute con i quasicristalli! Un esempio clamoroso di come ricerche matematiche a priori del tutto futili, ovvero del tutto interne alla matematica, siano divenute un punto fondamentale di riferimento per ricerche di fisica e cristallografia.
Nel 2011 il Nobel per la chimica fu assegnato a Shechtman per la scoperta dei quasicristalli. Successivamente se ne sono trovati allo stato naturale. L’articolo di Penrose con i disegni quasi periodici era stato pubblicato in origine su una rivista di studenti della Cambridge University Eureka, n. 39. Nel 1985 ho organizzato a Roma alla Sapienza il convegno su Escher. Del comitato organizzatore faceva parte anche Penrose che venne a Roma e come ho detto fece la felicità dei miei studenti di fisica, 50 di loro collaboravano al convegno per qualsiasi necessità ed erano sempre intorno a Penrose, sempre molto disponibile. Immagino che molti di loro, che sono divenuti fisici in giro per il mondo, saranno stati felici della notizia del Nobel. Gli atti del convegno vennero pubblicati da Elsevier-North Holland [10 ]R.Penrose, Escher and the Visual Representation of Mathematical Ideas, in H.S. M. Coxeter, M. Emmer, R. Penrose, M.L. Teuber, eds M.C. Escher: Art and Science, North-Holland, Elsevier Publ., Amsterdam (1986), p. 143-158 con l’appoggio del governo Olandese che ottenne, o meglio impose, alla fondazione Escher di non pretendere alcun diritto di autore delle immagini di Escher. Penrose era tra gli editor, oltre che scrivere l’articolo già citato. Parallelamente al convegno viene organizzata una mostra di opere di Escher all’Istituto Olandese di Valle Giulia a Roma dove Escher stesso era stato studente. La Regina d’Olanda inaugurò la mostra. Il piccolo catalogo andò esaurito subito [11 ]M. Emmer, J. Offerhaus, ed, M.C. Escher, Istituto Olandese, Roma, 1985, testi di G. Escher, M. Emmer, C. MacGillavry, D. Coxete.
Nel 1985 ho organizzato la mostra itinerante L’occhio di Horus: itinerari nell’immaginario matematico con la Citè des Sciences de la Villette e l’Istituto della Enciclopedia Italiana. Nel catalogo con il permesso di Penrose è stata inserita la versione italiana dell’introvabile articolo di Penrose su ricoprimenti non periodici pubblicato su Eureka [12 ]M. Emmer, ideazione e direzione scientifica, L’occhio di Horus: Itinerari nell’immaginario scientifico, Ist. Enciclopedia Italiana, Roma, 1989, testi tra gli altri di E. Giusti, P. Zellini, F.Clerici, L. Saffaro, M. Emmer, D. Coxeter, G. Francis, R. Penrose. Qualche anno dopo ebbi l’idea di pubblicare un numero speciale della rivista Leonardo, pubblicata sempre dalla Elsevier sulla Visual Math. Penrose scrisse un altro articolo intitolato On the cohomology of Impossible Figures [13 ]R. Penrose, On the cohomology of Impossible Figures, in M. Emmer, ed, The Visual Mind: Art and Mathematics, MIT Press, Boston, 1993. Nel frattempo la rivista era passata alla casa editrice MIT Press e il volume inaugurò la nuova serie dei Leonardo Books con il titolo The Visual Mind. Un secondo volume The Visual Mind 2 uscì nel 2005 sempre con la MIT Press.
Quando il film su Escher fu finito, (richiese anni dato che vi sono inserite numerose animazioni realizzate in 35 mm molto complesse e costose e la versione lunga di 50 minuti fu pronta solo nel 2000), fui inviato da Penrose al Institute of Mathematics di Oxford, per tenere una conferenza e proiettare il film. Purtroppo la macchina di proiezione prese fuoco ed anche il mio film, era una copia ovviamente. Quindi la proiezione non ebbe luogo.
In uno dei suo libri più famosi The Emperor’s New Mind [14 ]R. Penrose, The Emperor’s New Mind, Oxford University Press, Oxford, 1989 Penrose ha scritto: “Gli oggetti matematici non sono che concetti; sono le idealizzazioni mentali dei matematici, alle volte stimolate da taluni aspetti del mondo intorno a noi, ma sempre idealizzazioni mentali. Possono essere quindi altra cosa da semplici costruzioni arbitrarie della mente umana? Allo stesso tempo capita di frequente che vi siano legami profondi con la realtà, legami che vanno al di là delle possibili elaborazioni mentali di un qualsiasi matematico. Si ha l’impressione che il pensiero umano sia guidato verso una verità esterna ed eterna – una verità che esiste di per sé, e che si rivela solo parzialmente a qualcuno di noi.”
Sono molto felice della notizia del Nobel e sono molto lieto di avere avuto la fortuna di organizzare tante cose con Penrose, una persona gentilissima che mi sembra di aver incontrato solo pochi giorni fa, nel ricordo.
Lunga vita a Roger Penrose!
Michele Emmer
Note e riferimenti
| ⇧1 | J. Marsh, regia, The theory of Everything, con E. Redmayne, F. Jones, E. Watson, soggetto di Jane Wolde Hawking, sceneggiatura di Anthony McCarten, 123’, Working Title Films, UK-Giappone-USA (2014) |
|---|---|
| ⇧2 | M. Emmer, regia, Escher: Geometries and Impossible Worlds, seconda parte del film The Fantastic World of M. C. Escher, serie Art and Mathematics, con D. Coxeter, R. Penrose, C. Macgillavry, B. Ernst, sceneggiatura M. Emmer, 50’, prod. M. Emmer, 2000 |
| ⇧3 | L. S. Penrose e R. Penrose, Impossible Objects: A Special Type of Visual Illusion, vol. 49, n. 1, p 31-33 (1958) |
| ⇧4, ⇧10 | R.Penrose, Escher and the Visual Representation of Mathematical Ideas, in H.S. M. Coxeter, M. Emmer, R. Penrose, M.L. Teuber, eds M.C. Escher: Art and Science, North-Holland, Elsevier Publ., Amsterdam (1986), p. 143-158 |
| ⇧5 | M.C. Escher, The Graphic Work, MacDonald & C. Publ., London (1961) |
| ⇧6 | D. Schattshneider, M. C. Escher: Vision of Symmetry, Freeman, New York, 1990. |
| ⇧7 | D. Shechtman, I. Blech, D. Gratias, and J. W. Cahn. Metallic Phase with Long-Range Orientational Order and No Translational Symmetry, Phys. Rev. Lett., 53, 195, 12 November 1984 |
| ⇧8 | M. Emmer, regia, Symmetry and tessellations, serie Art and Mathematics, con R. Penrose, R. Vlad, M. Wurtz, sceneggiatura M. Emmer, 25’, prod. M. Emmer, 1980 |
| ⇧9 | M. Emmer, regia, Flatland, animazione, scenografia, sceneggiatura M. Emmer, 24’, prod. M. Emmer 2000; M. Emmer, ed., introduzione e postfazione, Flatlandia di E. A. Abbott con testo a fronte, con DVD del film (2008), senza DVD (2019), Bollati Boringhieri, Torino |
| ⇧11 | M. Emmer, J. Offerhaus, ed, M.C. Escher, Istituto Olandese, Roma, 1985, testi di G. Escher, M. Emmer, C. MacGillavry, D. Coxete |
| ⇧12 | M. Emmer, ideazione e direzione scientifica, L’occhio di Horus: Itinerari nell’immaginario scientifico, Ist. Enciclopedia Italiana, Roma, 1989, testi tra gli altri di E. Giusti, P. Zellini, F.Clerici, L. Saffaro, M. Emmer, D. Coxeter, G. Francis, R. Penrose |
| ⇧13 | R. Penrose, On the cohomology of Impossible Figures, in M. Emmer, ed, The Visual Mind: Art and Mathematics, MIT Press, Boston, 1993 |
| ⇧14 | R. Penrose, The Emperor’s New Mind, Oxford University Press, Oxford, 1989 |














applicare i disegni di Penrose alla poesia, intendo geometrizzare le parole nei versi e’ sempre stato nel mio lavoro di poeta presente se poi questo significa anche teatralizzare diviene piu’ affascinante-
Sono felicissima che il Professore Roger Penrose abbia vinto il premio Nobel per la Fisica.Le mie più vive congratulazioni.
L’ho sempre conosciuto come un matematico e ho lavorato molto nelle mie classi con i suoi moduli e i ricoprimenti del piano. Grande fisico, ma anche un matematico fantasioso nel muoversi in Geometria.
Ha donato molto a noi insegnanti.