Recentemente Archimede si è arricchito di una nuova rubrica, condotta da Roberto Zanasi: A colpo d’occhio.
Spesso le immagini ci permettono di capire qualcosa di più, o aggiungono nuovi significati alle formule, attivando altre modalità di ragionamento. A volte un disegno ci permette di sperimentare la famosa “esperienza ah-ha!”, quella che ci fa esclamare “ecco perché!”, o “finalmente ho capito!” (o, magari, “siamo sicuri che ho capito bene?”)
Ecco l’immagine di questo numero, che presenta una delle tante proprietà della sezione aurea.
E questa è la formula a cui si riferisce
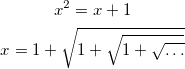
Il lettore è invitato a commentare sotto a questo post, offrendo la propria interpretazione.
I vari punti di vista offerti dalla trigonometria, dai numeri complessi e dalla geometria sintetica ci aiutano a capire meglio, a memorizzare con più efficacia, e ci insegnano a vedere le cose in un altro modo. E questo è il bello della matematica.
Roberto Natalini [coordinatore del sito] Matematico applicato. Dirigo l’Istituto per le Applicazioni del Calcolo del Cnr e faccio comunicazione con MaddMaths!, Archimede e Comics&Science.
La soluzione positiva della equazione di secondo grado e’ il numero aureo. Quindi la curva a “zig-zag” e’una rappresentazione grafica di come avvicinarsi a quell numero irrazionale. Similmente, la successione di radici (non so se ha un nome in Matematica) tende al numero aureo.
Una sola domanda: come si individuano i punti sugli assi visto che hanno a base la rq2?
Si parte da 1. Gli altri punti si individuano seguendo il percorso a zig-zag colorato in nero.