Una questione di dimensione

da Barbara Nelli | 25 Settembre 2022 | Ricerca | 1 commento

superfici così diverse che neppure l'aumento di dimensione non le fa apparire uguali

Alessia Cattabriga e Michele Mulazzani, professori di Geometria all’ Università degli studi di Bologna, commentano per Maddmaths! l’articolo di Quanta Magazine sulle superfici così diverse che neppure l’aumento di dimensione dello spazio che le ospita può farle apparire uguali.

Risale a pochi mesi fa, la soluzione di un problema formulato esattamente 40 anni fa dal matematico Charles Livingston, ora professore emerito della Indiana University. Il problema riguarda un particolare tipo di superfici, chiamate superfici di Seifert e ha a che fare con la dimensione. Il fatto che, quando studiamo alcuni oggetti geometrici, la dimensione dello spazio in cui stanno sia un fattore essenziale lo si capisce bene pensando, ad esempio, che in un piano due rette distinte che non sono parallele si incontrano per forza in un punto, mentre nello spazio non è più così. Lo spazio esiguo di un piano non permette infatti a due rette con direzioni diverse di evitarsi, ma avendo a disposizione una dimensione in più, cioè avendo la libertà di muoversi nello spazio tridimensionale, è possibile che accada.

In maniera analoga, Livingston si chiede se due superfici di Seifert che sono diverse nello spazio tridimensionale diventino uguali ogni volta che gli si fornisce più spazio, cioè se le si considera in uno spazio quadridimensionale. Ma cosa intende Livingston per uguali e diverse? L’equivalenza a cui è interessato si chiama isotopia continua ed è una deformazione graduale in cui NON si può strappare, NON si può cucire, NON si può incollare e NON si può tagliare. Ad esempio, non è difficile immaginare, e si può dimostrare, che la superficie di un pallone e di un cubo di Rubik siano isotope tra loro e non siano isotope alla superficie di una ciambella. In questo caso, però, non c’entra la dimensione perché è possibile dimostrare che la superficie di una ciambella e di un pallone sono diverse in tutte le dimensioni. Nel caso invece delle superfici di Seifert sembrava che la dimensione potesse essere un fattore determinante: infatti si conoscevano diversi esempi di coppie di superfici di Seifert che non si potevano deformare l’una nell’altra nello spazio a tre dimensioni, ma che invece diventavano isotope nello spazio a 4-dimensioni.

Nella figura seguente

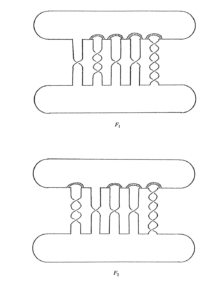
sono rappresentate schematicamente due superfici con tale proprietà: sono costituite da due dischi collegati da una serie di bande; non è troppo difficile (con un occhio molto allenato!) vedere che le bande al centro possono essere deformate le une nelle altre, mentre le parti rimanenti si attorcigliano, ma rimangono il bordo di un’onesta circonferenza e quindi, grazie ad alcuni risultati teorici, sono isotope in dimensione 4. A questo punto nasce spontanea la domanda di Livingston: sarà sempre così?

Prima di svelare la risposta, è necessario chiarire un altro punto, che riguarda le superfici di Seifert; tali superfici, a differenza di quelle richiamate sopra, sono superfici che hanno bordo, come ad esempio una cerchio che ha per bordo una circonferenza o una superficie cilindrica che ha per bordo due circonferenze. In particolare le superfici di Seifert oggetto della domanda di Livingston hanno un solo bordo o, in linguaggio più tecnico, hanno una sola componente di bordo, che sarà un’onesta circonferenza, come nel caso di un cerchio, o più in generale una “circonferenza annodata” come in questo caso.

Nodo Trifoglio

Più precisamente il bordo di queste superfici è un nodo matematico (ve ne avevamo già parlato qui https://maddmaths.simai.eu/ricerca/cosi-simili-eppure-cosi-diversi/) cioè un oggetto 1-dimensionale che modellizza ciò che si ottiene annodando una corda e poi incollando tra loro gli estremi liberi. La circonferenza è l’unico nodo non annodato, infatti si chiama anche nodo banale e ogni nodo, come la circonferenza, è il bordo di una superficie (in realtà più di una), che si chiama appunto superficie di Seifert per il nodo. Il nome è legato al matematico Herbert Seifert, vissuto nel secolo scorso, che nel 1934 descrisse un algoritmo per trovare, a partire dal nodo, una superficie che lo ha come bordo. Le coppie di superfici di Seifert oggetto della domanda di Livingston sono proprio superfici che hanno per bordo uno stesso nodo.

Ad esempio la coppia di superfici sopra rappresentate hanno come bordo un nodo che appartiene alla famiglia dei nodi di Pretzel …eh sì prendono il nome proprio dalle famoso e goloso pane teutonico!

Veniamo ora alla risposta, contenuta in questo preprint: esiste almeno una coppia di superfici di Seifert per cui la dimensione NON fa differenza, cioè non è possibile deformare l’una nell’altra neanche in uno spazio quadridimensionale. Il risultato è il frutto di una collaborazione, nata durante una conferenza a Providence lo scorso aprile, tra cinque matematici che lavorano in cinque diverse istituzioni tra Stati Uniti e Corea: Kyle Hayden della Columbia University, Seungwon Kim della Seul National University, Maggie Miller della Stanford University, JungHwan Park della Korea Advanced Institute of Science and Technology e Isaac Sundberg del Bryn Mawr College. In meno di due mesi i matematici hanno dimostrato che le due superfici rappresentate nella figura seguente.

non sono isotope neanche aggiungendo una quarta dimensione. Come hanno fatto? La costruzione si ispira ad una coppia di superfici

descritte da Herbert C. Lyon nel 1974 della cui isotopia quadridimensionale non si sapeva nulla. Miller, che già ci stava lavorando con Kim e Park, durante la conferenza raccontò l’idea a Hayden e Sundberg che, nei mesi precedenti, avevano ottenuto ottimi risultati legati ad un invariante chiamato omologia di Khovanov. Questo invariante permette di estrarre dati algebrici, facili da confrontare, da oggetti geometrici: se i dati algebrici sono diversi gli oggetti geometrici sono diversi in un senso un po’ più restrittivo dell’isotopia continua sopra descritta, che si chiama isotopia liscia. L’omologia di Khovanov è un invariante molto potente, ma può essere molto complesso da calcolare. Fortunatamente Hayden e Sundberg, grazie alle tecniche sviluppate, sono stati in breve tempo in grado di calcolarlo per l’esempio proposto da Miller., Kim e Park, constatando che le quantità algebriche erano differenti. A questo punto, convinti del fatto che l’esempio fosse quello giusto, il gruppo ha tentato di utilizzare invarianti più elementari legati all’isotopia continua, riuscendo nell’opera grazie ad una tecnica classica chiamata rivestimento ramificato. La dimostrazione di poche righe è davvero elegante e, come sottolineato dagli stessi autori, è sorprendente osservare che per risolvere una questione aperta da quarant’anni sia stato, alla fine, sufficiente utilizzare tecniche note alla comunità dei matematici da cinquant’anni!

Alessia Cattabriga e Michele Mulazzani

Immagine di copertina tratta da Hayden, Kyle and Kim, Seungwon and Miller, Maggie and Park, JungHwan and Sundberg, Isaac, Seifert surfaces in the 4-ball, https://arxiv.org/abs/2205.15283, 2022: The Seifert surface \(\Sigma^T_1\) obtained by band summing \(Wh(\Sigma_1) \) and a fiber for the trefoil (where the ellipsis indicates any number of full twists). The boundary of the surface is the knot \(K_T\).