Una mini-serie a cura di Marco Trombetti, in cui si esploreranno la tumultuosa storia e le incredibili vette raggiunte dalla matematica delle simmetrie: la teoria dei gruppi. In questo ultimo episodio parliamo di una delle vette più alte raggiunte dalla matematica di sempre, tenevi forte per: il teorema enorme.

 

It’s a rich, fascinating problem that has attracted many people for 150 years. I want to solve it because I want to solve it, not because it will benefit mankind. The solution of a significant problem is a great moment in the history of mathematics. Unfortunately, it is not going to give you a cure for cancer.
Daniel Gorenstein

Nel 1983, il matematico americano Daniel Gorenstein annunciava il completamento del progetto di classificazione dei gruppi semplici finiti. Oltre 100 furono i matematici coinvolti, circa 15.000 furono le pagine necessarie (contro le circa 200 necessarie per la dimostrazione dell’Ultimo Teorema di Fermat), poco meno di $10^{54}$ (e precisamente 808.017.424.794.512.875.886.459.904.961.710.757.005.754.368.000.000.000, circa mille volte il numero di atomi presenti nel nostro pianeta) è il mostruoso ordine di uno dei gruppi più speciali necessari alla classificazione (non a caso denominato “Il Mostro”).

Come si può facilmente immaginare tali numeri giustificano certamente l’appellativo di “teorema enorme” per questo risultato. Si tratta di un successo monumentale non solo per la matematica tutta, ma per l’umanità. “Ecco le vette del sapere che siamo in grado di raggiungere”, verrebbe da dire, e difatti, la classificazione ebbe un risalto tale che finì per attirare anche l’attenzione dei media non specializzati.

Tuttavia, oggi sappiamo che Gorenstein parlò un po’ troppo presto. Dati i numeri giganteschi e i molti ambiti distinti di ricerca che sono stati coinvolti nella dimostrazione, era (ed è ancora oggi) impensabile che una singola persona sia in grado di controllare tutta la dimostrazione — nemmeno con l’ausilio delle più moderne tecnologie.  Al giorno d’oggi la classificazione è stata ricontrollata (a pezzi) svariate volte, e tendenzialmente ha la fiducia dei matematici. Dico tendenzialmente perché nonostante sia frequentemente utilizzata, il suo uso viene allo stesso tempo esplicitato con frasi del tipo “questa dimostrazione fa uso della CGSF” (Classificazione dei Gruppi Semplici Finiti). Inoltre, allo studio attuale è una dimostrazione cosiddetta “di seconda generazione”, che dovrebbe avere il pregio di essere relativamente più facile della prima.

Ma cos’è un gruppo semplice?

Cominciamo subito col dire che il nome può trarre in inganno. Sebbene difatti alcuni gruppi semplici abbiano effettivamente una struttura facile da descrivere, la maggior parte non gode dello stesso privilegio, tutt’altro! Ora, se il lettore ha seguito le scorse puntate, saprà senz’altro cos’è un gruppo e cos’è un sottogruppo.

 

Sottogruppi normali

Alcuni sottogruppi però sono un po’ più speciali degli altri, e sono usualmente chiamati sottogruppi normali. Se $(G,\cdot)$ è un gruppo, allora un suo sottogruppo $H$ è detto normale nel momento in cui le sue traslazioni destre $Hx=\{hx : h\in H\}$ e sinistre $xH=\{xh : h\in H\}$ (usualmente dette laterali destri e sinistri) coincidono come insiemi (non necessariamente elemento per elemento) per ogni $x\in G$.

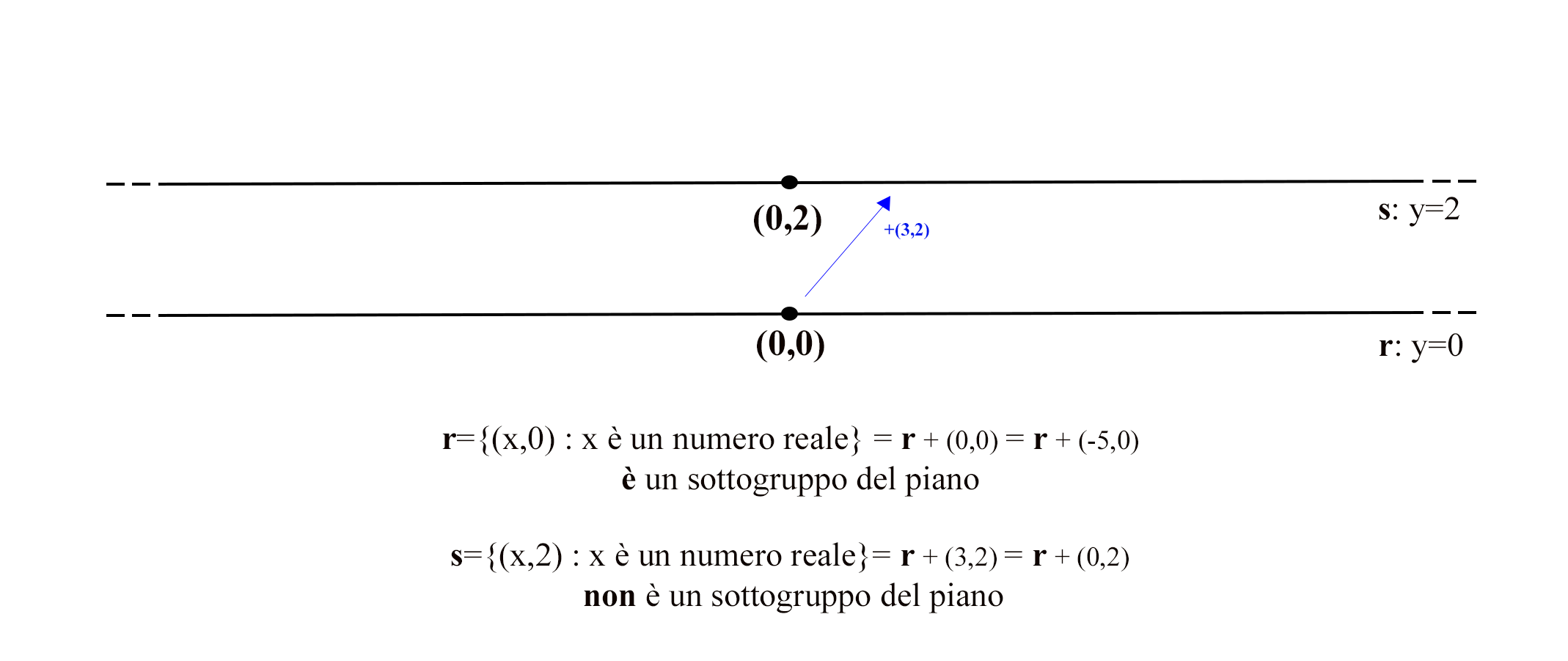
Mi spiego meglio, consideriamo il piano cartesiano $(\mathbb R\times\mathbb R,+)$ con l’usuale somma vettoriale. In questo caso, l’insieme delle coppie che definiscono una retta r passante per l’origine forma un sottogruppo, diciamo $r$. Essendo che ora siamo in notazione ‘‘additiva’’ (cioè l’operazione di gruppo è denotata con il $+$ e non con il $\cdot$), i laterali si scrivono come segue: $r+x$ e $x+r$. Vediamo ora di chiarire cosa rappresentino.

Da un lato, $r+x$ vuol dire prendere la retta e spostare ogni punto rispetto alla direzione indicata da $x$, mentre $x+r$ vuol dire prendiamo il punto $x$ e sommiamolo (cioè trasliamolo) di volta in volta rispetto ai punti individuati dalla retta $r$. Se queste due operazioni restituiscono lo stesso insieme di punti dello spazio, allora il sottogruppo è normale. Ovviamente, nel caso in questione, poiché l’addizione è commutativa, si ha banalmente che $x+r=r+x$ sempre, sicché tutte le rette per l’origine sono in realtà sottogruppi normali.

Un esempio meno banale potrebbe essere quello seguente. Torniamo a considerare le simmetrie del triangolo equilatero.

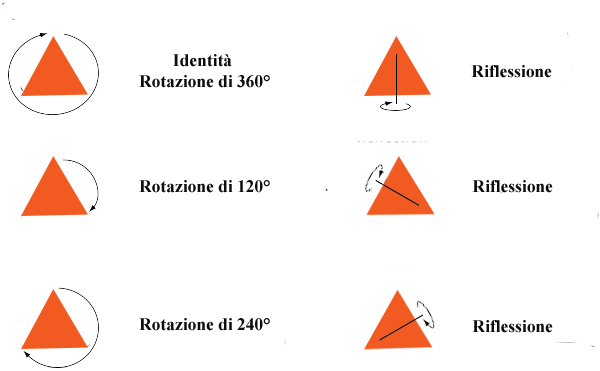
Il sottogruppo $R$ delle rotazioni è un sottogruppo normale. Infatti prendiamo ad esempio la prima riflessione e chiamiamola $\tau$. Non è difficile computare che il prodotto della rotazione di 120° e di $\tau$ è uguale al prodotto di $\tau$ e della rotazione di 240°. Similmente si mostra che $R\cdot\tau=\tau\cdot R$ e quindi che $R$ è normale. Similmente si può ripetere il ragionamento per un altro qualsiasi movimento al posto di $\tau$ e quindi $R$ è normale. Se consideriamo invece il sottogruppo costituito solo da $\tau$ e dall’identità, questo non è normale in quanto se $r$ è la rotazione di 120°, allora risulta che $\tau+r$ è diverso sia da $r+\tau$ che da $r$.

 

Perché i sottogruppi normali sono speciali?

Ciò che rende speciali i sottogruppi normali è il fatto che consentono di studiare a pezzi la struttura del gruppo. Infatti, ogniqualvolta abbiamo un sottogruppo normale $N$ di un gruppo $G$, allora l’insieme dei laterali $xN$ (destri o sinistri che siano, tanto coincidono) forma un nuovo gruppo con l’operazione ‘‘indotta’’ (cioè $xN\cdot yN=xyN$) che si denota con $G/N$. Consideriamo di nuovo l’esempio del piano $(\mathbb R\times\mathbb R,+)$ e prendiamo l’asse delle ascisse $r=\{(a,0) : a\in \mathbb R\}$ come sottogruppo (normale). Ora l’insieme dei laterali è l’insieme delle rette parallele alla retta $r$ e ogni retta parallela a $r$ è individuata univocamente da un valore dell’ordinata.

Come si sommano dunque due laterali (o due rette parallele)? Basta considerare il valore delle ordinate che identifica le rette, sommarlo, e andare a considerare la retta parallela passante per quel valore dell’ordinata. Quindi in fin dei conti il gruppo quoziente assomiglia molto (è isomorfo) a $(\mathbb R,+)$. Poiché anche banalmente $(r,+)$ è isomorfo a $(\mathbb R,+)$, siamo riusciti con l’ausilio di un sottogruppo normale a “spezzare” lo studio di $(\mathbb R\times\mathbb R,+)$ in quello più facile di due gruppi isomorfi ad $(\mathbb R,+)$. Questa però non è la fine della storia, perché un conto è sapere come sono fatti questi mattoncini più facili in cui il gruppo di partenza si divide, mentre un altro è capire come tali mattoncini possano attaccarsi. Per la nostra storia, quest’ultimo aspetto però non ci riguarda.

 

Torniamo alla definizione di gruppo semplice

A questo punto possiamo definire un gruppo semplice come un gruppo non-triviale i cui unici sottogruppi normali siano quelli banali, cioè ${1}$ e il gruppo totale. Dall’esempio precedente è evidente che se $G$ è un gruppo finito e $N$ è un suo sottogruppo normale, allora $G$ si spezza in due gruppi più facili (quantomeno di ordini inferiori) $N$ e $G/N$. Se $N$ non è semplice allora esiste un sottogruppo proprio non-triviale $H$ tale che $N$ si “spezza” nei due gruppi $H$ e $N/H$.

Continuando in questo modo si perviene facilmente al fatto che in ultima analisi ogni gruppo finito è costruito a partire da gruppi semplici. Il teorema enorme classifica tutti questi mattoncini, che sono dunque i componenti fondamentali della teoria dei gruppi, un po’ come in chimica gli elementi della tavola periodica di Mendeleev sono i componenti fondamentali della materia. Proprio questa analogia fu sfruttata dal matematico Ivan Andrus per spiegare al padre ciò di cui si occupava, costruendo a questo scopo una “tavola periodica” dei gruppi semplici finiti.

Il teorema di classificazione dei gruppi semplici finiti asserisce che i gruppi semplici finiti sono esattamente quelli indicati in questa tavola. La rappresentazione utilizzata nella costruzione della tavola si fonda principalmente sulla distribuzione della maggior parte dei gruppi semplici finiti in famiglie omogenee. Andiamo ora a descrivere brevemente alcune di queste classi di gruppi.

 

Le famiglie facili

La colonna verde a destra rappresenta i gruppi ciclici finiti di ordine primo. Se ricordate il teorema di Lagrange, questo assicura che ogni sottogruppo ha ordine divisore dell’ordine del gruppo. Dunque un gruppo di ordine primo deve necessariamente essere semplice perché i suoi sottogruppi avranno ordine o $1$ o quello di tutto il gruppo.

Un’altra famiglia che abbiamo già avuto modo di vedere è quella dei gruppi alterni di grado maggiore o uguale a $5$. Questi sono gruppi semplici e sono praticamente il motivo per cui le equazioni dal grado $5$ in poi non sono risolubili per radicali.

 

I gruppi di tipo Lie

Continuando ora la nostra analisi dei gruppi semplici che si trovano nella parte “continentale” della tavola periodica, ciascuna delle colonne, a partire dalla seconda, rappresenta una famiglia di gruppi semplici cosiddetti di tipo Lie (dal nome del matematico norvegese Sophus Lie, il quale, pur non occupandosi direttamente di gruppi semplici, considerò certe tipologie di gruppi in qualche senso relazionabili a tali famiglie).

I gruppi di tipo Lie si distribuiscono in 16 famiglie, ciascuna delle quali contiene infiniti gruppi semplici, che risultano “parametrizzabili” in modo simile. Infatti, alcune di queste famiglie richiedono una dimensione e un campo per specificare un gruppo: ad esempio, nella seconda colonna sono descritti gruppi del tipo PSL(n,q), cioè essenzialmente gruppi di matrici $n\times n$ con determinante 1, su un campo di ordine q. Altre famiglie richiedono per essere definite solamente un campo (spesso molto particolare): tale è ad esempio il caso della decima colonna, dove si trovano i gruppi di Suzuki Sz(q), su un campo il cui ordine q è potenza di 2 con esponente dispari maggiore di 1.

 

Gli sporadici

Nelle due righe verdi in basso troviamo $26$ gruppi semplici particolari, cosiddetti sporadici, che non possono essere ricondotti ad alcuna delle famiglie precedentemente descritte. Tale designazione fu introdotta nel 1911 da William Burnside: “Questi gruppi semplici apparentemente sporadici richiederebbero probabilmente un esame più attento di quello che hanno ricevuto finora’’. Gli sporadici non sono però del tutto scollegati tra di loro e di fatti ecco rappresentate di seguito le ‘‘relazioni’’ che vi intercorrono.

 

Come si evince facilmente dal diagramma, c’è un gruppo semplice che sovrasta gli altri, il gruppo Mostro. Il Mostro ci permette di fornire un’altra analogia con la tavola degli elementi di Mendeleev. Infatti l’esistenza di tale gigante (amichevole) fu prevista da Bernd Fischer nel 1973 e dimostrata da Robert Griess nel 1982. Una situazione del tutto analoga a quella del germanio. L’insieme dei gruppi semplici che sono ‘‘contenuti’’ nel mostro fu battezzato famiglia felice, mentre i 6 al di fuori hanno preso il nome di paria.

Abbastanza sorprendentemente, una congettura del 1992 di Richard Borcherds pone il gruppo Mostro in contatto con alcune questioni di analisi complessa. Tale congettura fu nominata il ‘‘Mostruoso Chiaro di Luna’’ (Monstrous Moonshine) da John Conway (l’ideatore del gioco della vita: provate a cercare game of life su google) e Simon Norton (la cui singolare vita da matematico-barbone è descritta nel libro di Masters ‘‘Un genio nello scantinato’’).

Piccole curiosità. Non c’è dubbio che Damiano dei Måneskin conosca la teoria dei gruppi. Come recita il tatuaggio attorno al collo? Esatto, ‘‘Il ballo della vita’’. E cosa vuol dire Måneskin se non Moonshine? Non vi ho convinti? Beh, chiedetelo direttamente a lui!

Da notare anche che il gruppo sporadico B subito sotto al Mostro è detto baby Mostro, e che tale era il nome con cui il figlio di Conway era stato denominato dai suoi studenti. Inoltre, Conway e Norton sono tra gli autori principali di un vero e proprio atlante dei gruppi semplici finiti (l’ATLAS of Finite Groups).

 

 

Fine?

Si potrebbe continuare a discorrere all’infinito della teoria dei gruppi e dei suoi attori, ma, ahimè, come quasi tutto a questo mondo, anche questa miniserie deve giungere ad una fine. Voglio però congedarmi con l’augurio che quanto scritto possa essere di stimolo a tutti i giovani appassionati di matematica per approfondire certi aspetti dell’algebra astratta ed in particolare della teoria dei gruppi. Per quanto (indubbiamente, nda) affascinante, la teoria dei gruppi, come ogni altra branca del sapere teorico, può continuare a vivere solo grazie ai continui sforzi di coloro i quali vogliano farsi carico delle sue difficili bellezze.

Poco altro può offrirvi qualcosa di così certo e così maestoso, qualcosa su cui si possa sempre fare affidamento, qualcosa che possa accompagnarvi nei momenti bui e in quelli belli, qualcosa che possa offrire sprazzi di eternità a vite che sono state troppo brevi. Studiate ragazzi. A presto.