La gestione delle risorse è uno dei temi più dibattuti in questo periodo. I modelli matematici possono fornire un supporto per le scelte da fare. È il caso delle risorse ittiche con il modello di Ricker.
La gestione delle risorse è uno dei tempi più dibattuti negli ultimi anni. Dall’energia agli allevamenti, passando per acqua e agricoltura, la questione è ampia e complessa, ma anche urgente. Quest’anno l’Earth Overshoot Day è fissato al primo agosto, ossia per quel giorno l’umanità avrà esaurito le risorse prodotte dalla Terra per il 2024. Dal 2 agosto il bilancio per il nostro pianeta sarà negativo. Definire un’accorta gestione delle risorse significa conoscere l’evoluzione delle risorse, ed è qui che vengono in aiuto i modelli matematici. Per gli allevamenti ittici c’è il modello di Ricker.
William Edwin (Bill) Ricker è stato un entomologo canadese. È ritenuto il fondatore della della moderna scienza delle risorse ittiche. In questo contesto ha sviluppato il modello che porta il suo nome, presentato nell’articolo “Stock and recruitment” del 1954. Per questi motivi ha ricevuto diversi riconoscimenti nel corso della sua carriera.
Passiamo al modello.
Consideriamo una specie ittica. Sia \(N_{t}\) il numero di individui all’istante \(t\). Inoltre, siano \(r\) il tasso di crescita e \(K\) la capacità portante dell’ambiente (carrying capability, in inglese), ossia il numero massimo di individui della specie che l’ambiente può sostenere. Il modello di Ricker fornisce il numero di individui all’istante \(t+1\) noti quelli all’istante \(t\), oltre che i parametri biologi del sistema, \(r\) e \(K\):
\[N_{t+1}=N_t \,e^{\displaystyle r \left(1-\frac{N_t}{K}\right)}.\]
Si tratta di un modello discreto. Assegnato un valore iniziale \(N_0\) è possibile conoscere l’evoluzione della popolazione ittica considerata. Ad esempio, in Figura 1 è riportata una popolazione con taglia iniziale \(N_0=10\), capacità portante \(K=1000\) e crescita \(r=0.3\). La popolazione cresce fino ad arrivare asintoticamente al limite \(K\), simile a quanto accade con una logistica.
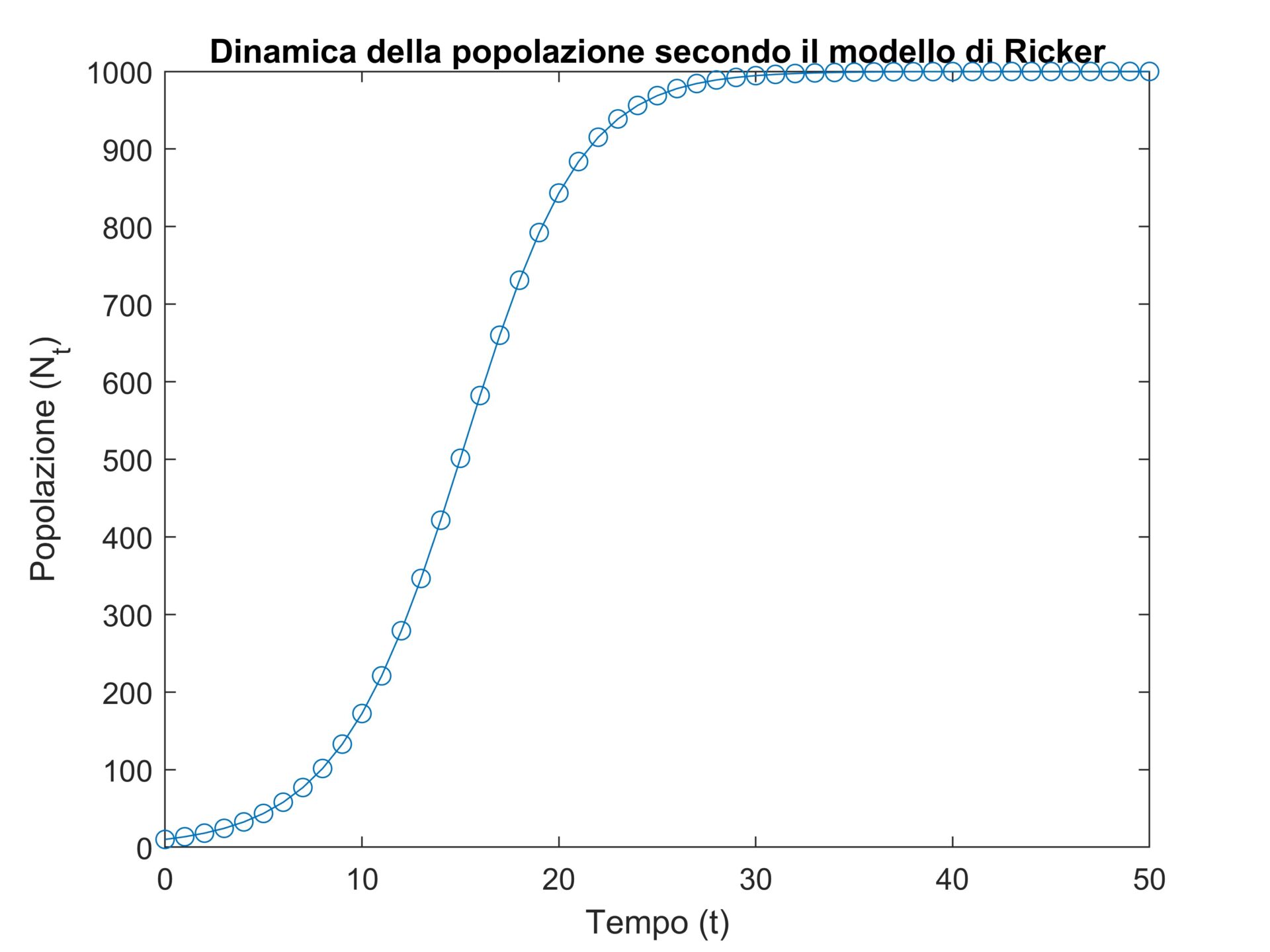
Figura 1. Modello di Ricker con tasso di crescita \(r=0.3\).
Consideriamo la stessa specie con stessa taglia iniziale \(N_0=10\) e capacità portante \(K=1000\), ma assumiamo una crescita \(r=2\). La nuova evoluzione della popolazione secondo il modello di Ricker è mostrata in Figura 2. Inizialmente la popolazione cresce avvicinandosi a \(K\) come nel caso precedente. Da un certo tempo, cominciano delle oscillazione intorno a \(K\), fino poi schiacciarsi su questo valore per tempi lunghi. A differenza del caso logistico, con il modello di Ricker la taglia della popolazione, \(N(t)\), può oltrepassare il valore limite \(K\). In questo caso si parla (ancora) di fenomeno di overshoot. La popolazione supera la sostenibilità ambientale, ma è poi forzata a ridursi nuovamente.
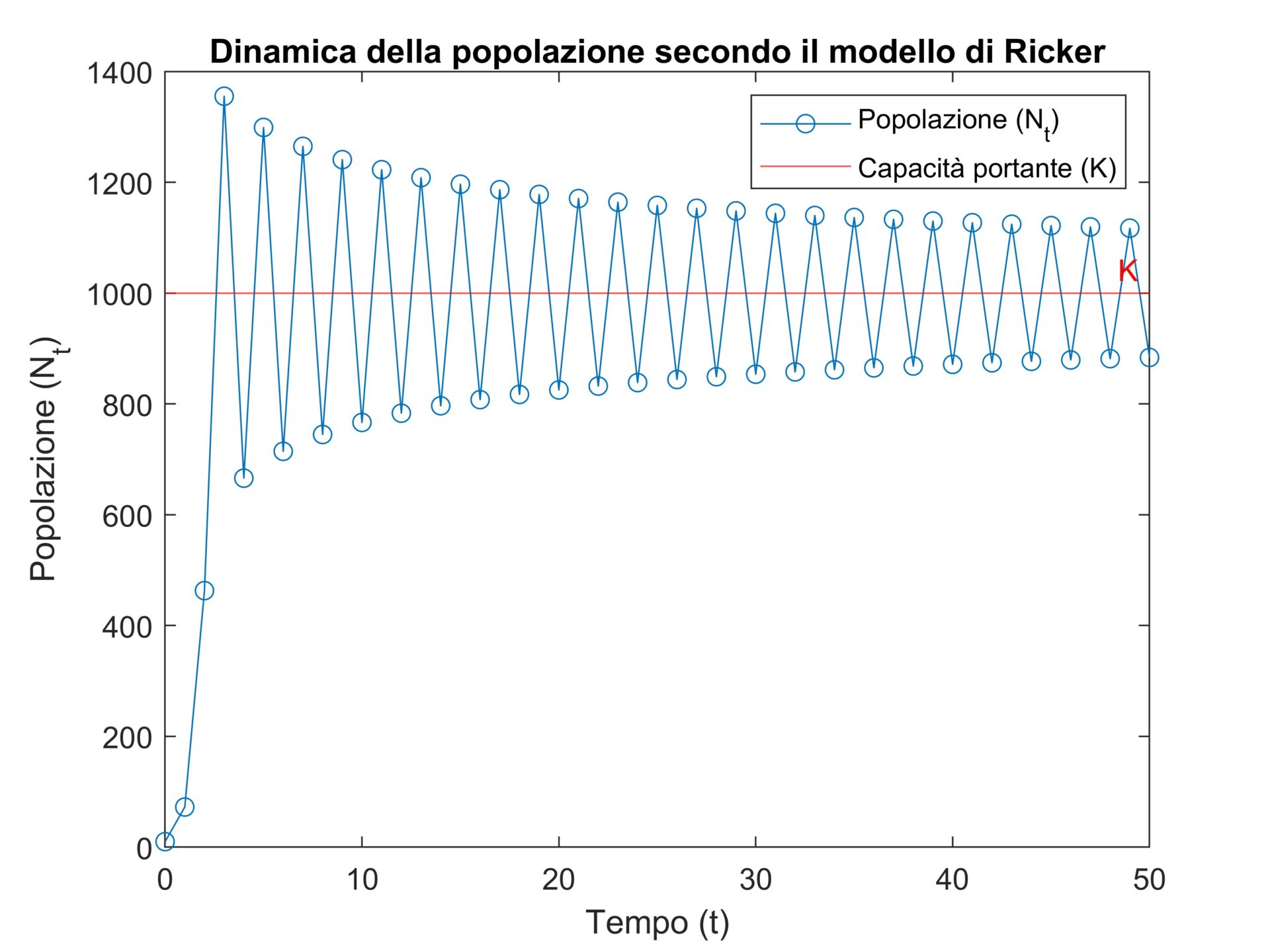
Figura 2. Modello di Ricker con tasso di crescita \(r=2\). La popolazione \(N(t)\) supera il limite \(K\).
Nel 1969 Ricker ha utilizzato il modello nell’articolo “Food from the sea” per fare delle prime stime di quantità sostenibili di pesce da prelevare dal mare. Il modello è stato ulteriormente arricchito nel corso del tempo, ad esempio inserendo effetti competitivi, così da aderire sempre meglio alla realtà e fornire previsioni sempre più accurate per scelte più attente.























