Il modello Lotka-Volterra descrive l’evoluzione di un sistema a due specie: prede e predatori. Ma come evolve il tasso di consumo delle prede in funzione del loro numero? Il modello di Holling descrive questa dinamica. Ce ne parla Marco Menale.
Il ruolo modellistico della matematica lo ritroviamo anche in ecologia. Il (tanto famoso) modello preda-predatore o Lotka-Volterra descrive l’evoluzione di un ecosistema costituito da due sole specie: prede e predatori. Nei suoi cent’anni di storia è stato ampliato e arricchito così da essere sempre più realistico e versatile. È il caso della sua versione competitiva, in cui più specie competono per una stessa risorsa. Nella forma originale, le prede hanno crescita malthusiana, salvo poi ridursi per effetto dei predatori. Tuttavia, più aumentano i predatori più si trovano a competere tra loro per le risorse, ossia le prede. Conoscere il tasso di consumo di prede da parte dei predatori è un’informazione importante. Interviene qui il modello di Holling (o functional response, dall’inglese).
Crawford Stanley “Buzz” Holling è stato un ecologista e professore canadese alla University of Florida. Oltre che premiato a livello internazionale, è considerato uno dei fondatori della moderna ecologia economica. Senza andare troppo in profondità, è un modo di guardare all’economia in funzione dell’ecosistema globale e del benessere collettivo, oltre che delle risorse.
Per modello di Holling si intende la descrizione del tasso con cui i predatori consumano prede in funzione del quantitativo di queste ultime. Holling propose tre diverse risposte funzionali (da cui il nome inglese) per modellare questo tasso (Figura 1).
La risposta funzionale di tipo I è
\[ R(N) = aN,\]
dove \( R(N) \) è il tasso di consumo, \( a \) è la probabilità di incontro tra predatore e preda e \( N \) è il numero di prede disponibili. È un modello lineare, con consumo costante di prede da parte dei predatori, senza limiti di saturazione. È una descrizione utile per organismi come le porifere, che possono catturare prede in modo proporzionale alla loro abbondanza. Tuttavia, la sua semplicità lo rende poco versatile.
Il modello di tipo II fa fronte alla precedente mancanza di limite di saturazione. Il tasso di consumo non può, in generale, aumentare all’infinito, poiché c’è un tempo per catturare, mangiare e digerire la (povera) preda. La risposta funzionale di tipo II è
\[ R(N) = \frac{aN}{1 + ahN}, \]
dove \( h \) è il tempo utile per consumare la preda. A piccoli valori di \( N \), il comportamento è quasi lineare, ma per grandi \( N \), il tasso di consumo si avvicina a un valore massimo (\displaystyle\frac{1}{h}), detto tasso di saturazione. Questo modello è comune in predatori come ragni e rapaci, che impiegano un tempo nella gestione delle prede.
Infine, la risposta funzionale di tipo III fornisce un comportamento ancora più complesso, descritto dalla curva sigmoidea
\[ R(N) = \frac{aN^k}{1 + ahN^k}, \qquad k>1.\]
C’è ancora un limite di saturazione come nel tipo II. Tuttavia, a differenza di quest’ultimo, il predatore è inefficiente quando le prede scarseggiano; ma, aumenta la sua efficienza con la crescita di \( N \). Questo può essere dovuto all’apprendimento del predatore o al fatto che le prede diventano più vulnerabili in gruppo. Si osserva questo comportamento in alcuni mammiferi che sviluppano strategie più efficaci man mano che la caccia procede.
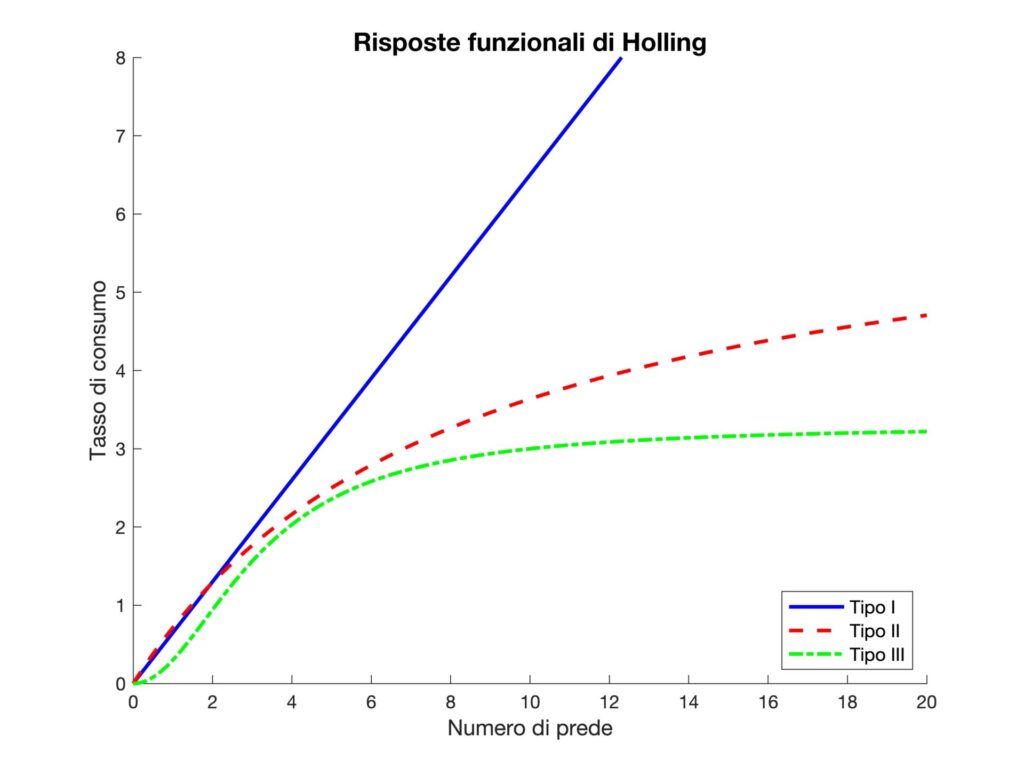
Figura 1. I tre tipi di risposta funzionale di Holling.
Il modello di Holling si è dimostrato cruciale (e continua ancora a esserlo) nella modellazione matematica delle dinamiche ecologiche. È versatile e ben si adatta a diverse situazioni, anche complesse. Aumenta così, con i modelli ecologici, la nostra comprensione dei meccanismi della natura, fino a prevedere (con tutti i limiti del caso) come le specie rispondono ai cambiamenti ambientali o all’intervento umano.



















