La crisi delle risorse è uno dei temi principali degli ultimi anni. La matematica può fornire degli scenari di gestione. È il caso del modello di Gordon. Ce ne parla Marco Menale.
La crisi delle risorse è solo accelerata dall’invasione ucraina della Russia. Il prezzo della benzina vola così come quello del gas importato in Europa. Non da ultimo si aggiunge il problema del grano ucraino destinato a molti paesi del nord-Africa. E poi ci sono le materie prime (come il silicio) necessarie per realizzare i microchip di cui sono pieni smartphone, tablet, orologi, pc e gran parte del nostro quotidiano. La matematica può aiutarci a capire le dinamiche e le conseguenze della gestione di una risorsa. Ad esempio con il modello di Gordon.
Scott Gordon è stato un economista canadese. Durante la carriera accademica ha insegnato alla Carleton University e tenuto scuole estive di storia dell’economica alla Queen’s University. Si è interessato anche di walfare e scienze sociali. Tuttavia uno dei suoi principali contributi riguarda il problema della gestione delle risorse.
Siamo agli inizi degli anni ‘50. Il governo canadese incarica Gordon di studiare l’impatto della pesca sia sull’ecosistema che sull’attività economica. Analizza il fenomeno scrivendo un modello simile al Lotka-Volterra. E raccoglie i risultati nell’articolo “The Economic Theory of a Common-Property Resource: The Fishery”.
Passiamo al modello. Indichiamo con \(x(t)\) la quantità di un certo pesce a disposizione all’istante \(t\) e con \(y(t)\) l’investimento economico e di forza lavoro per la pesca. Questi due quantità evolvono in accordo al seguente sistema di equazioni differenziali ordinarie del primo ordine:
\[
\begin{cases}
x'(t)=F(x)-q\,y(t)\,x(t)\\\\
y'(t)=k\, \left(p\,q\,y(t)\,x(t)-c\,y(t)\right)
\end{cases}
\]
Il modello dipende da diversi parametri. \(F(x)\) rappresenta il tasso di crescita di quel pesce e ha la forma \(F(x)=x\cdot T(x)\), dove \(T(x)\) è la differenza tra tasso di natalità e di mortalità. Mentre \(q\) è il coefficiente di cattura, ad esempio il numero di pescherecci utilizzati, e \(c\) ne rappresenta il costo. Infine \(p\) è il prezzo sul mercato di unità di pesce e \(k>0\) una costante di sensibilità al profitto. In questo modello la pesca non è soggetta ad al alcuna regola.
Il sistema ammette il seguente punto d’equilibrio, definito da Gordon come equilibrio bioeconomico:
\[(x^*,\,y^*)=\left(\frac{c}{pq},\, \frac{pF(x^*)}{c}\right)\].
La quantità di pesce \(x^*\) diminuisce assieme al costo \(c\). Infatti costi bassi per i pescherecci determinano una maggiore pesca. Ma \(x^*\) può essere molto basso anche se a crescere è il prezzo \(p\) del pesce o il coefficiente di cattura \(q\) (figura 1). Inoltre c’è uno scarso profitto economico.
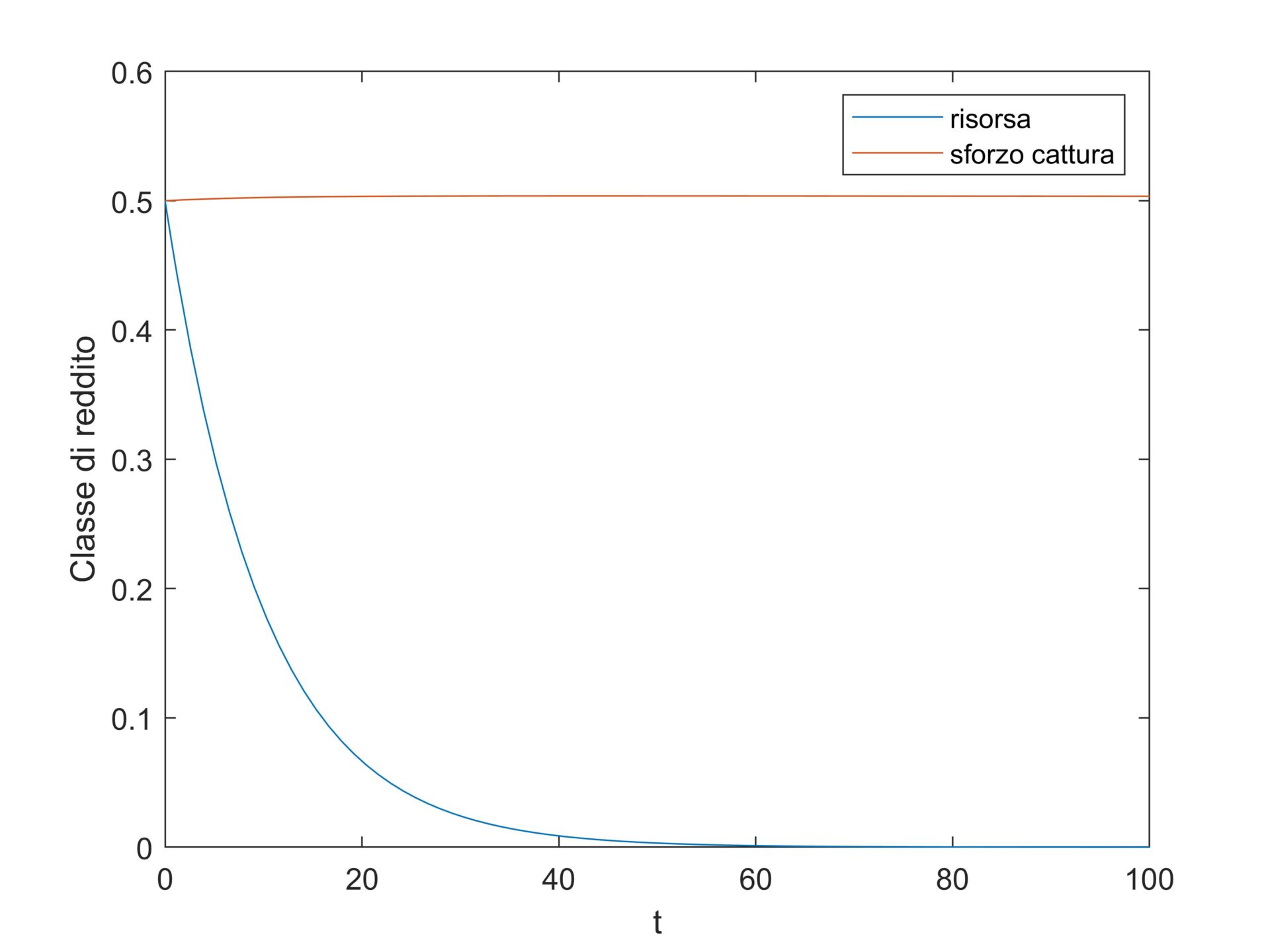
Figura 1. Simulazione del modello di Gordon. Andamento di risorse \(x(t)\) e sforzo di cattura \(y(t)\)
Dove nascono i problemi? Per Gordon è la mancanza di regolamentazione della pesca. Da un lato la risorsa viene velocemente prosciugata. Dall’altro c’è anche un danno economico. L’economista canadese suggerisce una regolamentazione sia sul piano biologico che economico. E questa non può che arrivare dal legislatore, ossia lo Stato.
Al modello di Gordon ne sono seguiti altri nei decenni successivi. Si è dato così avvio ad una nuova scienza: la Bioeconomia matematica. Tuttavia alcune risorse continuano ad essere usate intensivamente. Ma due anni di pandemia e una guerra nel cuore dell’Europa hanno riportato il problema delle risorse in primo piano. E i modelli matematici possono fornire possibili scenari di confronto.























