Le partite di calcio si preparano e si discutono a colpi di dati. Per i goal c’è la distribuzione di Poisson. Ce ne parla Marco Menale per La Lente Matematica.
È ricominciato il campionato di serie A, da quest’anno in compagnia di una nuova Champions League. Assieme alle partite ricominciano le discussioni tra tifosi. Che sia in una trasmissione televisiva o al bar della colazione, sono numeri e dati a farla da padrone. E non solo tra i tifosi: squadre e allenatori si avvalgono di team di data analyst per le loro scelte. Poiché a contare nel calcio sono i goal, fatti e subiti, diversi dati si concentrano proprio su di loro. Qui arriva in aiuto la matematica, con la distribuzione di Poisson.
Partiamo dall’aspetto matematico. La distribuzione di Poisson, che deve il suo nome al matematico e statistico francese Siméon-Denis Poisson, è una distribuzione di probabilità discreta. Misura la probabilità che si verifichi un certo numero di eventi in un intervallo di tempo o spazio, quando questi eventi accadono in modo indipendente l’uno dall’altro e con una frequenza costante. In formule, sia \(\lambda>0\) la frequenza degli eventi, la probabilità che se ne verifichino \(n\) secondo la distribuzione di Poisson è
\[P_{\lambda}(n)=\frac{\lambda^n\, e^{-\lambda}}{n!}.\]
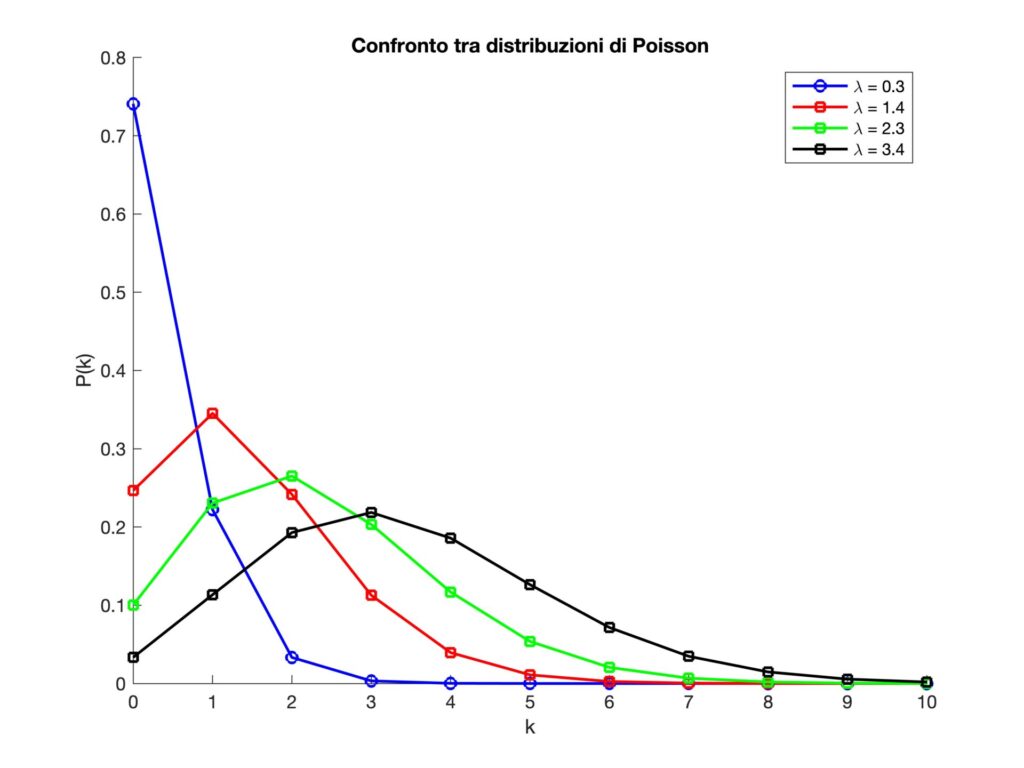
Figura 1. Andamento della distribuzione di Poisson al variare del parametro \(\lambda\).
Torniamo al calcio. Supponiamo di conoscere la media goal a partita di una squadra. Allora, considerato come evento il goal segnato e \(\lambda\) la media, possiamo usare la distribuzione di Poisson per calcolare la probabilità che la squadra segni \(n\) di goal in una singola partita. Facciamolo con dati reali presi dallo scorso campionato. L’Inter campione d’Italia ha segnato \(89\) goal, con una media di \(2,34\). Così la distribuzione di Poisson associata (Figura 2), posto \(\lambda=2,34\), è
\[P(n)=\frac{2,34 ^n\, e^{-2,34}}{n!}.\]
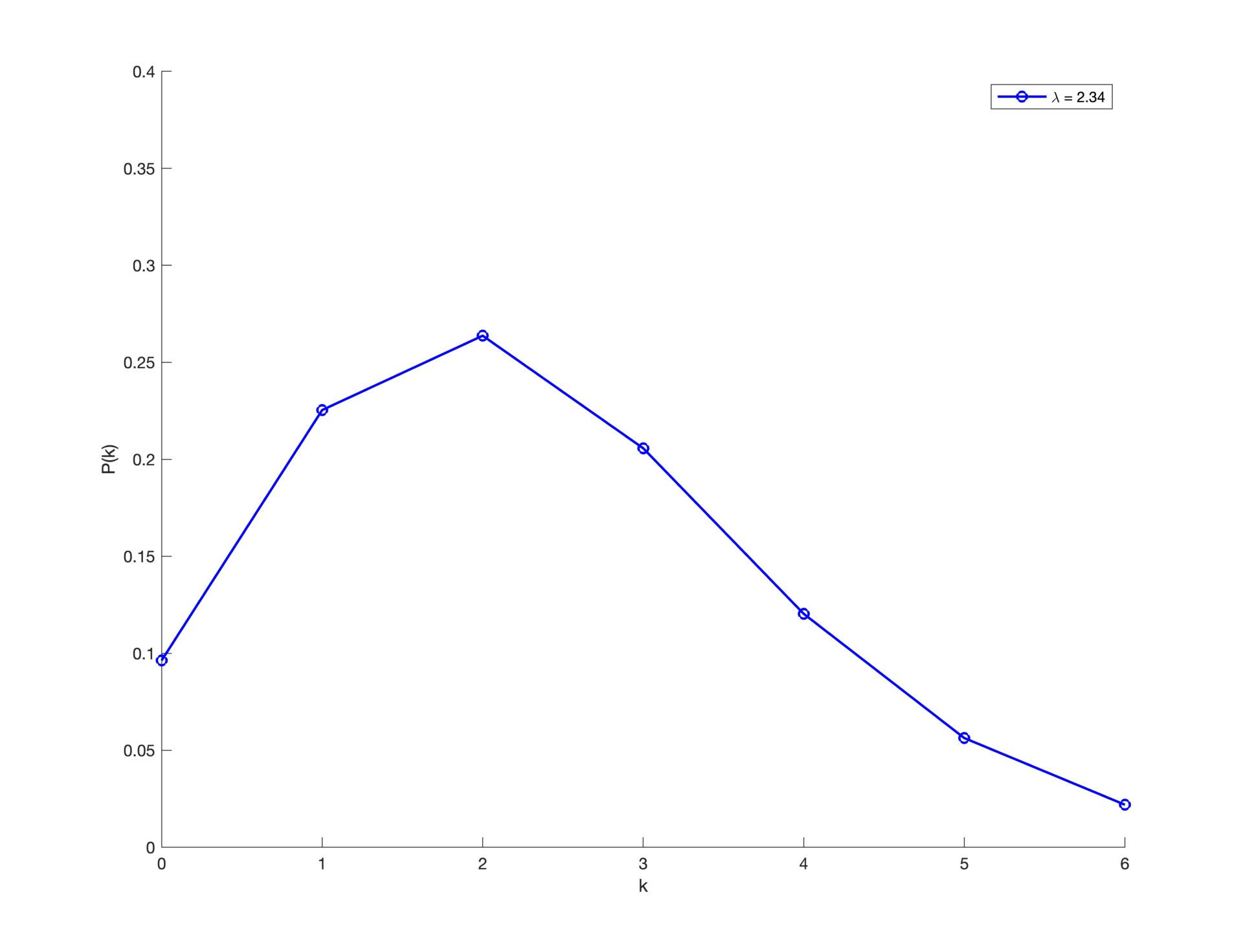
Figura 2. Distribuzione di Poisson dei goal fatti dall’Inter nella Serie A 2023/2024. Fonte: FootyStats.
Quindi, le probabilità con cui l’Inter segnava rispettivamente \(0,\, 1,\, 2\, 3\, 4\) goal a partita sono
\[
\begin{align*}
P(0) & \approx 0,0963\\
P(1)& \approx 0,2254\\
P(2)& \approx 0,2637\\
P(3)& \approx 0,2057 \\
P(4)& \approx 0,1203.
\end{align*}
\]
I valori più alti sono intorno alla media, come ci si aspetta. Per l’Inter era poco probabile (meno del \(10\%\) finire una partita senza segnare goal. A confronto, era più probabile che ne segnasse \(4\) di goal in una partita. In figura 3 è rappresentata la distribuzione di Poisson dei goal subiti dall’Inter, che erano in media \(0,58\). La forma è molto diversa se paragonata a quella dei goal fatti. Non c’è nessuna gobba, ma un rapido avvicinamento allo \(0\), ossia bassa probabilità di prendere goal. Infatti, è stato molto difficile segnare all’Inter nel passato campionato. Questi due dati aiutano a spiegare il perché della vittoria finale.
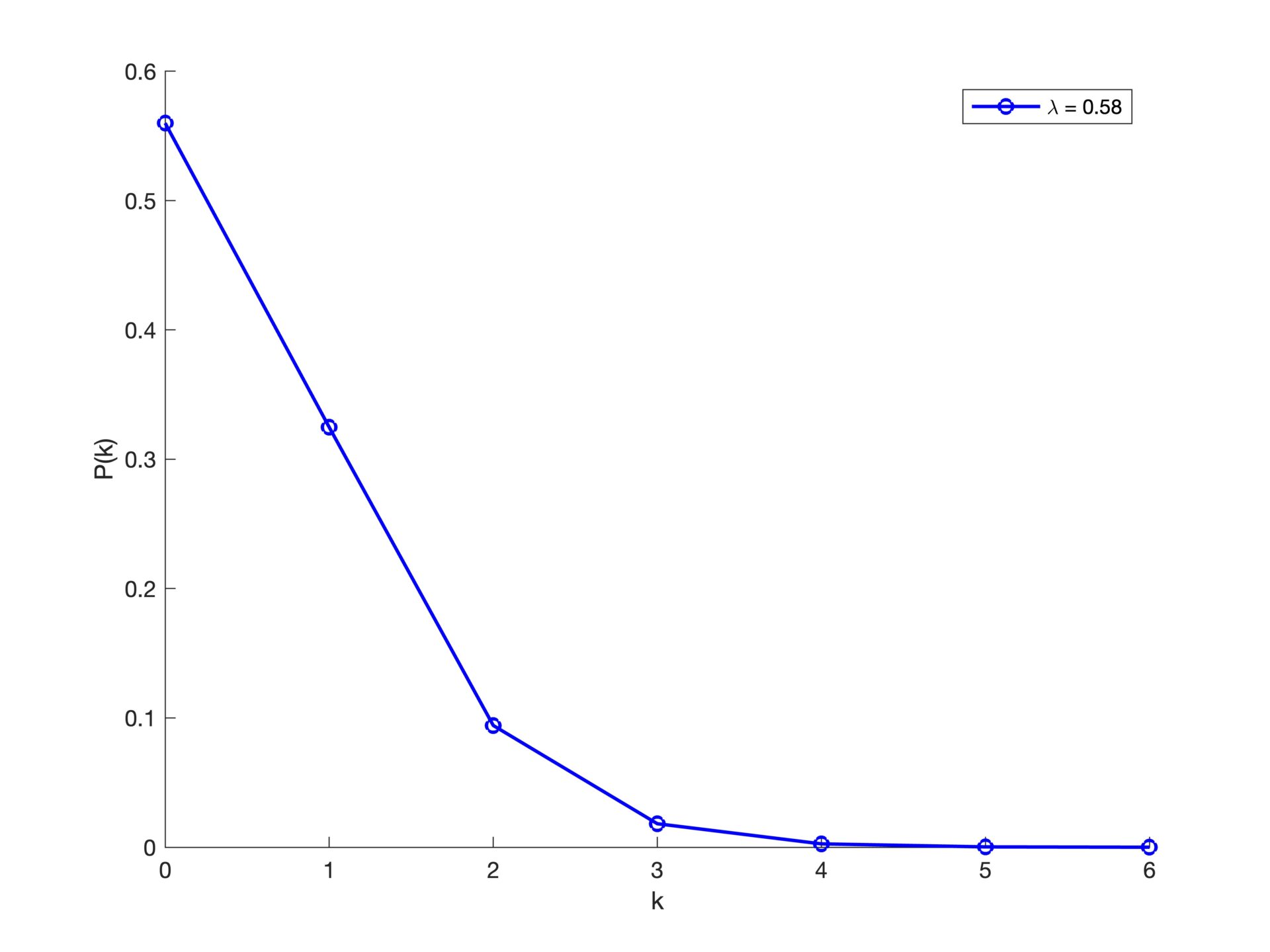
Figura 3. Distribuzione di Poisson dei goal subiti dall’Inter nella Serie A 2023/2024. Fonte: FootyStats.
L’uso della distribuzione di Poisson presenta dei limiti modellistici. L’ipotesi di indipendenza degli eventi non è molto realistica: potrebbe essere più difficile segnare il primo goal in una partita che il quarto quando la difesa avversaria è già sotto la doccia. Tuttavia, come accade con altri parametri (tra cui l’xG), la distribuzione di Poisson può aiutare allenatori e staff nelle loro scelte. Ad esempio, osservare come cambia la forma della distribuzione nel corso della stagione può fornire suggerimenti su eventuali correttivi in corso d’opera.
Chi vuole divertirsi nel corso di questo campionato può costruire di volta in volta la distribuzione di Poisson dei goal della propria squadra, o delle altre, con i dati aggiornati di Opta Analyst.



















Salve, questo ragionamento tiene conto solo ed esclusivamente dei gol fatti da una squadra. Come si può modificare il modello prendendo in considerazione anche la media dei gol subiti dalla squadra avversaria? Le faccio notare che spesso, quando si affrontano squadre dall’alto potenziale sia offensivo che difensivo, il calcolo di poisson conduce a probabilità sull’over molto alte, ma spesso sono le difese a prevalere.
Vorrei capire se matematicamente devo moltiplicare le medie (Fatti contro subiti) oppure farne la media (Fatti+Subiti / 2).
Grazie mille
Questo modello, se così possiamo dire, è una visione “in media”. Se, invece, vuole qualcosa di puntuale, ossia capire quanti goal “è probabile” che la squadra in questione faccia contro un’altra determina squadra, allora la Poisson deve rientrare in uno schema più ampio. Serve un approccio diverso, così come l’ntroduzione di altri parametri. Ad esempio, si possono considerare parametri come come gli xG, con le loro varianti. Tornerò su questo argomento nelle prossime uscite.