La corsa agli armamenti comporta dei rischi. Il modello di Richardson spiega matematicamente questo fenomeno. Ce ne parla Marco Menale.

Febbraio 2022. La pandemia sembra giunta al termine e le persone tirano un respiro di sollievo. Ma arriva una nuova sciagura. La guerra ci sconvolge ogni giorno. Le immagini dalle città ucraine lasciano senza parole. La situazione è complessa. Eppure una domanda sconvolge tutte e tutti. Ci sarà la terza guerra mondiale? Nessuno possiede la sfera di cristallo. Ma  la corsa agli armamenti non fa ben sperare. Ci sono modelli matematici per lo studio e la descrizione di questo fenomeno.

Lewis Fry Richardson è stato un matematico, fisico e meteorologo britannico. È uno dei primi a sviluppare modelli meteorologici, prima ancora di Edward Norton Lorenz (qui per approfondire). Richardson presta servizio come infermiere durante la prima guerra mondiale. E in questa fase raccoglie le idee per sviluppare un modello matematico per la corsa agli armamenti.

È il 1919. Richardson pubblica “Mathematical psychology of war”. Siano \(x\) ed \(y\) le quantità di armamenti di due nazioni. La sua ipotesi è la dipendenza lineare dell’incremento di armamenti di una nazione rispetto agli armenti di un’altra. Allora scrive un sistema quadratico di equazioni differenziali:

\[
\begin{cases}x’(t)=k\cdot y-a\cdot x+g \\\\
y’(t)=l\cdot x-b\cdot y+h\end{cases}\]

Guardiamo nel dettaglio i termini. \(k\) ed \(l\) sono i parametri che descrivono la dipendenza degli armamenti di una nazione rispetto a quelli dell’altra. \(a\) e \(b\) sono fattori sociali e possono frenare la corsa agli armamenti. Infine \(g\) e \(h\) misurano i valori morali e ideali. In generale le soluzioni del sistema di Richardson sono esponenziali (figura 1).

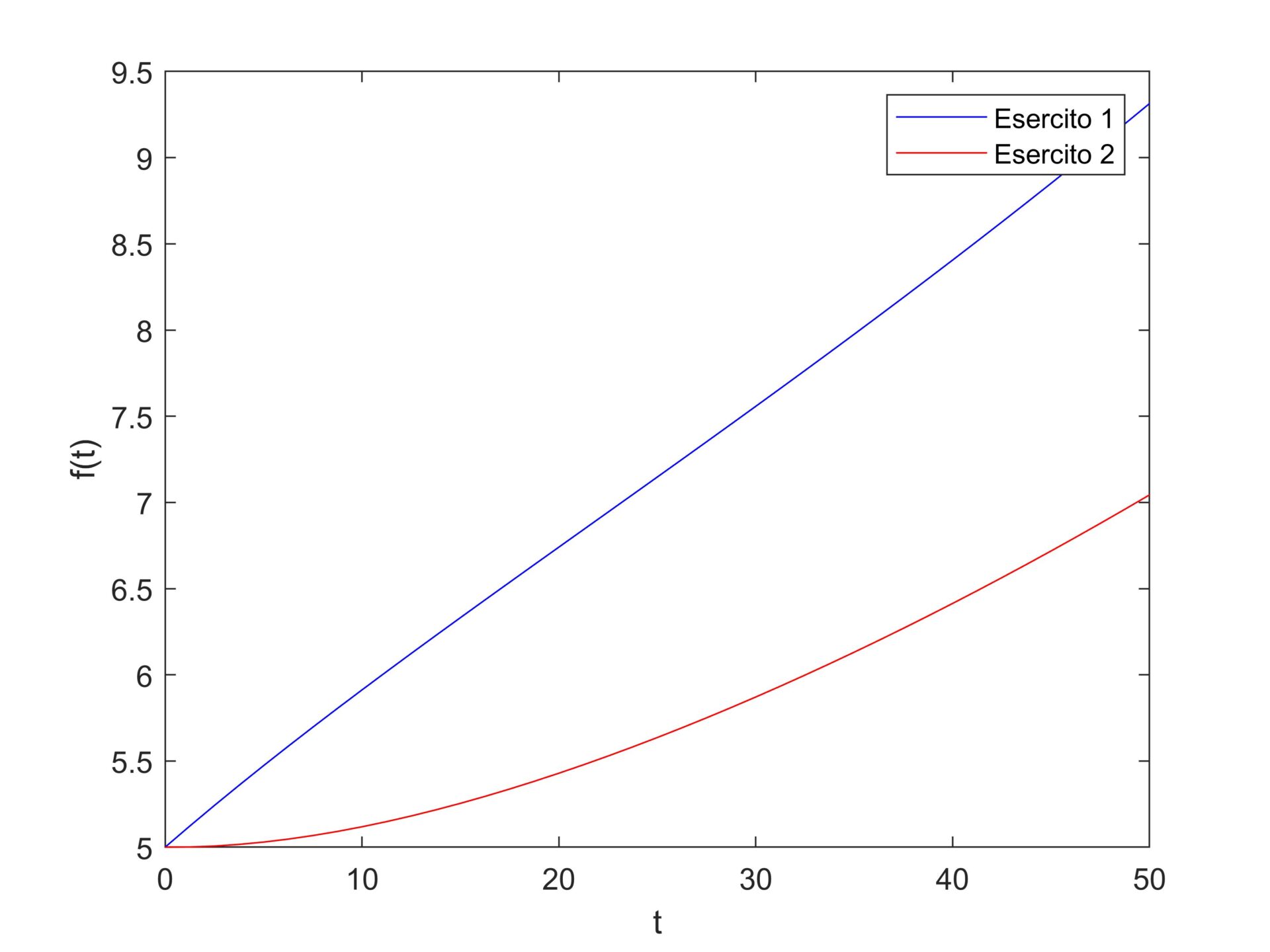
Figura 1. Le curve degli armamenti secondo il modello di Richardson

Il modello di Richardson è chiaro. La corsa agli armamenti di una nazione determina una corsa anche per l’altra. E questo significa rischiare un’escalation. La parte morale ed etica può fermare questa corsa dalle imprevedibili conseguenza. Tuttavia i sei parametri del modello ne rendono difficile l’applicazione a situazioni reali e ben definite.

Ma non è tutto qui. Richardson osserva quanto accade tra la prima e la seconda guerra mondiale. In quel periodo la corsa agli armamenti è sfrenata.  Conclude che il mutuo disarmo di due avversari non è condizione sufficiente per mantenere la pace. Infatti la pace è possibile solo se ci sono condizioni di reciproca fiducia e soddisfazione. E questo significa studiare i punti di equilibrio del sistema di equazioni di Richardson.

Modelli più raffinati sono apparsi nei decenni successivi. L’arrivo delle armi nucleari ha creato ulteriori parametri da tenere in considerazioni. Ad esempio nei modelli di Kaye e Zane si considera il peso di queste armi. E in questi casi i punti di equilibrio dipendono proprio dalla loro disponibilità.

La matematica non può rispondere alle sciagure di questo periodo. Tuttavia i suoi modelli sono un modo per capire e descrivere quanto succede. E il modello di Richardson è un suggerimento dei pericoli di una nuova corsa agli armamenti.

[Un sentito ringraziamento per i consigli e i suggerimenti al professore Antonino Drago e al professore Gerardo Toraldo]

Marco Menale