Le partite di calcio si guardano sempre più con i numeri. Basti pensare a quante volte sentiamo i telecronisti parlare di xG, expected goals, di un’azione o di una squadra. Ma come si misura l’xG? Tra gli altri, con l’angolo di tiro. Ce ne parla Marco Menale.
Guardiamo le partite di calcio con i numeri. Sempre più dati a disposizione consentono di valutare le prestazioni di quell’attaccante o le scelte di quell’allenatore. Succede con gli expected goals (xG), attualmente uno dei dati più citati, prima, durante e dopo i novanti minuti. Questo numero misura la probabilità che una certa occasione di gioco si trasformi in goal. Uno dei parametri utilizzati per il calcolo dell’xG è l’angolo di tiro.
Per angolo di tiro si intende l’angolo tra la posizione della palla, in possesso di un calciatore durante il tiro, e le estremità della porta avversaria, ossia i due pali.
Osserviamo la Figura 1.

Figura 1. Rappresentazione dell’angolo di tiro \(\theta\). Fonte: Karim, H., & Marwane, L. The Kos Angle, an optimizing parameter for football expected goals (xG) models. International Journal of Computer Science in Sport, 22(2), 49-61.
Immaginiamo un sistema cartesiano centrato nel calcio d’angolo di sinistra. Il calciatore che sta tirando è nella posizione \(A(x,y)\), mentre i due pali sono in \(C(x_C,0)\) e \(B(x_B,0)\), rispettivamente. Conoscere l’angolo di tiro significa determinare il valore dell’angolo \(\theta\). Partiamo dalle tre distanze \(AB,\, AC, \, BC\) che valgono, rispettivamente:
\[\begin{align*}
AB&=\sqrt{(x-x_B)^2+y^2}\\\\
AC&=\sqrt{(x-x_C)^2+y^2}\\\\
BC&=|x_b-x_b|.
\end{align*}
\]
Applicando il teorema di Carnot o del coseno, otteniamo il valore di \(\theta\):
\[\theta=\arccos \left[\frac{2y^2+(x-x_B)^2+(x-x_C)^2-(x_B-x_C)^2}{2\sqrt{\left((x-x_B)^2+y^2\right)\cdot\left((x-x_C)^2+y^2\right)}}\right].\]
Immergiamo tutto ciò nei dati reali. Partiamo da un campo di calcio largo \(50 \,m\). Fissata una larghezza di \(7 \,m\) per la porta, le coordinate dei pali diventano: \(C(21.5,\,0)\) e \(B(28.5,\, 0)\). Inoltre, supponiamo che il calciatore tiri da una distanza di \(22 \,m\) dalla linea di fondo, ossia poco fuori dall’aria di rigore. Quindi, le sue coordinate diventano \(A(x,\, 22)\). A questo punto, dalla formula precedente possiamo ottenere i valori dell’angolo di tiro \(\theta\) al variare della solo coordinata \(x\), ossia la posizione in larghezza del calciatore (Figura 2.).
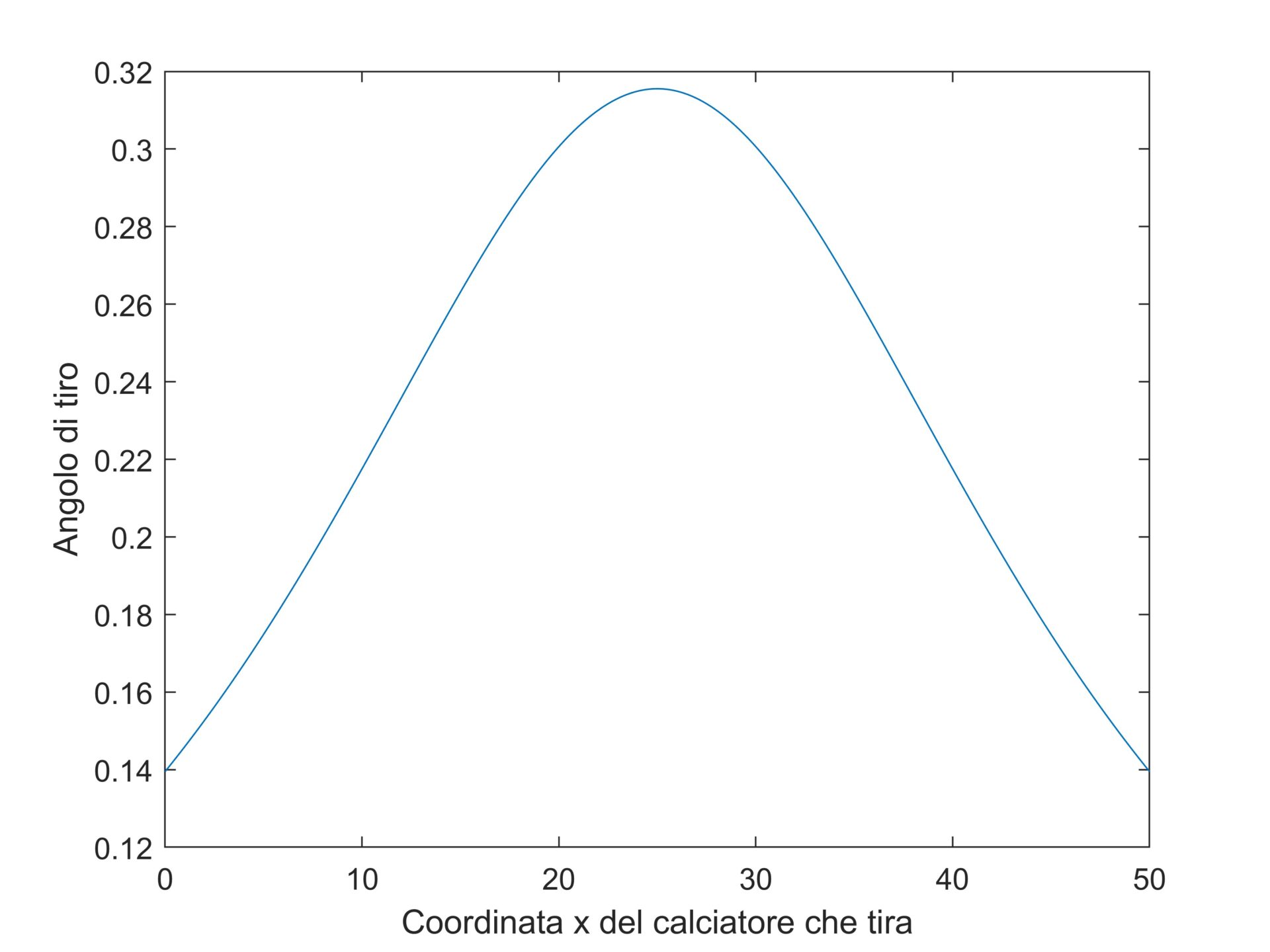
Figura 2. Angolo di tiro \(\theta\) in funzione della coordinata \(x\).
La coordinata \(x\) varia da \(0\, m\) a \(50\, m\), data la larghezza del campo. Agli estremi, \(x=0\, m\) e \(x=50\, m\), l’angolo di tiro è minimo; quelle posizioni sono le più complicate per trovare la porta. Il massimo è raggiunto al centro, quando il calciatore è esattamente sulla metà, in ampiezza, del campo, ossia \(x=25\, m\). Da questa posizione \(\theta\) ha valore massimo; come si dice in gergo “ha più specchio della porta a disposizione”. Quanto più si accentra, più aumenta \(\theta\). Infatti, vediamo spesso gli esterni di centrocampo e di attacco accentrarsi per trovare la conclusione, piuttosto che tirare direttamente dalla posizione di cross. In questo modo aumentano l’angolo di tiro. E, di conseguenza, l’xG dell’azione.
Le considerazioni precedenti spiegano perché l’angolo di tiro sia uno dei parametri di calcolo dell’xG. Come analizzato, all’accentrarsi della posizione l’angolo di tiro aumenta, e, quindi, l’xG. Tuttavia, questa è solo una prima approssimazione. Ad esempio, per una stima più precisa non è possibile trascurare i calciatori difendenti tra chi tira e la porta. Si passa così a versioni più complicate dell’angolo di tiro, come l’angolo di Kos (Kos Angle, in inglese). Inoltre, ci sono anche altri fattori da considerare come qualità del calciatore al tiro e momento della partita, solo per citarne alcuni. Così è possibile avere stime sempre più accurate dell’xG; come più accurati diventano i dati con cui vedere le partite di calcio.


















