A maggio di quest’anno, Joshua E. Green e Andrew Lobb (articolo su arXiv) hanno compiuto un interessante passo avanti nella dimostrazione della Congettura di Toepliz. La congettura di Toepliz è una di quelle congetture matematiche che hanno tutte le caratteristiche necessarie per affascinare il grande pubblico: è semplice da enunciare in termini elementari, ma terribilmente difficile da dimostrare (o confutare). Aggiungiamo a tutto ciò il fatto che tratta di un problema geometrico facile da visualizzare e che le soluzioni di sue versioni più semplici sono ottenute tramite l’uso della topologia, e c’è tutto il materiale per una bella storia. La storia è infatti stata raccontata più volte, da 3blue1brown, da QuantaMagazine e, in italiano, sul blog di Francesco Polizzi. In questo articolo Alberto Saracco cerca di fare il punto della situazione.
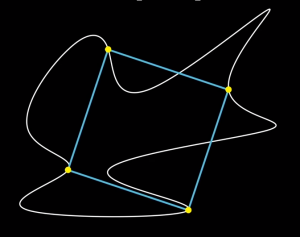
La congettura di Toepliz (o del quadrato inscritto)
Congettura del quadrato inscritto Data una qualsiasi curva piana chiusa senza autointersezioni (chiusa e semplice o curva di Jordan, in linguaggio più tecnico) \(\gamma\), allora c’è almeno un quadrato inscritto in \(\gamma\), ovvero 4 punti di \(\gamma\) che sono i vertici di un quadrato.
(vedi immagine, tratta dal video di 3blue1brown).
Questa congettura è stata posta da Otto Toepliz nel 1911 e resiste ormai da oltre un secolo. Per alcune curve è particolarmente semplice trovare un quadrato inscritto, e può perfino capitare che i quadrati inscritti siano infiniti (come capita ad esempio se \(\gamma\) è una circonferenza o un quadrato). La congettura è stata inoltre risolta positivamente per curve regolari a tratti, ovvero fondamentalmente con un numero finito di punti in cui la tangente della curva non è ben definita, come per esempio i poligoni:
Teorema del quadrato inscritto Data una qualsiasi curva piana chiusa senza autointersezioni regolare a tratti \(\gamma\), allora c’è almeno un quadrato inscritto in \(\gamma\), ovvero 4 punti di \(\gamma\) che sono i vertici di un quadrato.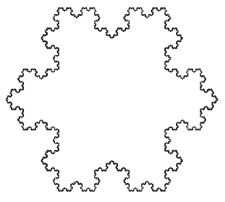
La parte difficile è dimostrare il risultato per curve decisamente irregolari (e difficilmente immaginabili), come ad esempio il fiocco di neve di Koch (vedi figura a lato, da wikipedia). Ovviamente il fiocco di neve di Koch è estremamente simmetrico ed è facile trovare un quadrato inscritto in quella specifica curva.
La congettura del rettangolo inscritto
Quando una congettura è difficile da dimostrare è una pratica comune cercare di dimostrarne una sua versione più debole, ad esempio rafforzando l’ipotesi (come visto sopra, richiedendo che la curva sia regolare a tratti) oppure indebolendo la tesi, come nel caso della congettura del rettangolo inscritto:
Teorema del rettangolo inscritto Data una qualsiasi curva piana chiusa senza autointersezioni (chiusa e semplice o curva di Jordan, in linguaggio più tecnico) \(\gamma\), allora c’è almeno un rettangolo inscritto in \(\gamma\), ovvero 4 punti di \(\gamma\) che sono i vertici di un rettangolo.
(vedi immagine, tratta dal video di 3blue1brown).
La dimostrazione del teorema del rettangolo inscritto
La dimostrazione di questa congettura è particolarmente elegante e indicativa del come funziona la matematica, dato che è una dimostrazione che passa da settori della matematica apparentemente molto distanti: in particolare la dimostrazione di un “rigido” risultato di geometria Euclidea passa attraverso la molto più “duttile” topologia. Potete ammirare la dimostrazione, attraverso bellissime animazioni, guardando il video di 3blue1brown. Dopo la visione del video, passate alla sezione successiva Il nuovo teorema).
Se invece preferite leggere la dimostrazione, continuate a leggere. Tutte le figure sono tratte dal video di 3blue1brown e la linea dimostrativa che seguo ricalca fedelmente quella del video.
Il primo passo nella dimostrazione consiste nel riscrivere la tesi in una maniera diversa, ma equivalente. Un quadrilatero è un rettangolo se e solo se le sue diagonali sono congruenti e si intersecano nel loro punto medio (vedi immagine).
Pertanto per dimostrare il teorema del rettangolo inscritto, dimostreremo che esistono due coppie di punti distinti (A,B) e (C,D) sulla curva, tali che \(\overline{AB}=\overline{CD}\) e i due segmenti \(AB\) e \(CD\) hanno lo stesso punto medio.
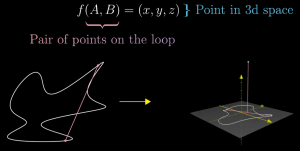Consideriamo una funzione \(f\) dalle coppie di punti della curva nello spazio \(\mathbb R^3\) costruita come segue: se \(A,B\) sono due punti della curva, sia \(M\in\mathbb R^2\) il loro punto medio e \(d\) la lunghezza del segmento \(AB\). Allora (vedi figura)
\(f(A,B) \ =\ (M,d)\in\mathbb R^2\times\mathbb R=\mathbb R^3\)
Trovare il rettangolo inscritto, o le due coppie di punti sulla curva che condividono punto medio e distanza, equivale a dimostrare che la funzione \(f\) non è iniettiva. Bisogna però fare attenzione a cosa si prende come dominio della funzione \(f\): banalmente \(f(A,B)=f(B,A)\), ma tali punti costituiscono un rettangolo banale, ovvero un segmento. Non è una vera soluzione al nostro problema, più di quanto il “quadrato” \((A,A,A,A)\) (ovvero un singolo punto) sia una soluzione al problema originario. Pertanto, dobbiamo considerare come dominio della funzione \(f\) le coppie non ordinate di punti sulla curva, ovvero considerare equivalenti le coppie \((A,B)\) e \((B,A)\).
Osserviamo che la funzione \(f\) è continua, quindi siamo interessati a capire che spazio topologico rappresenta le coppie non ordinate di punti della curva \(\gamma\). Poiché siamo interessati semplicemente alla topologia, la curva chiusa e semplice \(\gamma\) è la stessa cosa di una circonferenza \(\mathbb S^1\). Pertanto le coppie (ordinate) di punti sono rappresentate da \(\mathbb S^1\times\mathbb S^1\), ovvero da un toro (vedi figura).
Per capire quale è la superficie che rappresenta le coppie non ordinate di punti in \(\gamma\) c’è un po’ di lavoro da fare. Iniziamo col rappresentare il toro che rappresenta le coppie ordinate di punti come un quadrato con la consueta identificazione dei lati (vedi figura).
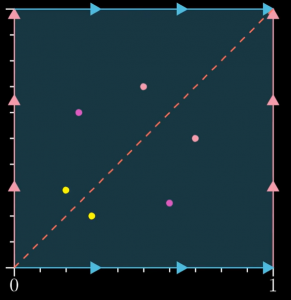Dobbiamo poi identificare i punti \((x,y)\) con \((y,x)\), ovvero piegare il quadrato lungo la diagonale \((x,x)\) ottenendo come luogo rappresentante le coppie non ordinate di punti sulla curva con un triangolo con due lati da identificare (i lati rosa e blu da identificare sono stati attaccati insieme da questa operazione, e ora indichiamo i lati da identificare in viola). La linea rossa tratteggiata rappresenta le coppie di punti della forma \(x,x\).
Per identificare quei due lati, effettuiamo un taglio (in giallo in figura), e attacchiamo insieme i due lati viola.
Ciò risulta in un quadrato con due lati opposti da identificare, con orientazione opposta, ovvero un nastro di Moebius \(\mathcal M\).
Le coppie ordinate di punti sono rappresentate da un toro, mentre le coppie non ordinate sono rappresentate da un nastro di Moebius \(\mathcal M\), il cui bordo (rosso in figura) rappresenta le coppie \(A,A\).
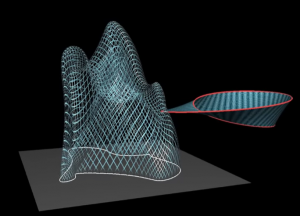Pertanto dobbiamo capire come la funzione \(f:\mathcal M\to\mathbb R^3\) può mandare in maniera continua il nastro di Moebius in \(\mathbb R^3\). Osserviamo che poiché i punti del bordo del nastro (in rosso) rappresentano una finta coppia di punti (ovvero uno stesso punto ripetuto), \(f\) manda tali punti \((A,A)\) in punti del piano: \((A,0)\). In effetti, il punto medio del “segmento” \(AA\) è \(A\) stesso e \(A\) dista \(0\) da sè stesso.
Quindi vogliamo mandare in maniera continua il nastro di Moebius nel semispazio superiore di \(\mathbb R^3\) in modo che il suo bordo venga mandato nella curva chiusa \(\gamma\times\{0\}\subset\mathbb R^3\). Questo non è possibile senza autointersezioni del nastro di Moebius (questo fatto, sebbene intuitivo, necessita di un uso maggiore della topologia per una dimostrazione rigorosa). E ciò vuol dire che due punti del nastro di Moebius vengono mandati da \(f\) nello stesso punto di \(\mathbb R^3\), ovvero che ci sono due coppie di punti di \(gamma\) che hanno lo stesso punto medio e la stessa distanza. Ovvero, c’è un rettangolo inscritto in \(\gamma\), qualunque sia \(\gamma\) curva piana chiusa e semplice. Q.E.D.
Il nuovo teorema
Joshua E. Green e Andrew Lobb a maggio non hanno dimostrato la congettura del quadrato inscritto, ma hanno migliorato notevolmente la dimostrazione nel caso in cui \(\gamma\) sia una curva regolare a tratti. In questo caso, non solo –come già noto– la congettura del quadrato inscritto ha risposta positiva, ma vale molto di più. Precisamente:
Teorema dei rettangoli inscritti (Green-Lobb 2020) Sia \(\gamma\) una qualsiasi curva piana chiusa senza autointersezioni e regolare a tratti e \(R\) un rettangolo qualsiasi (eventualmente anche un quadrato), allora c’è almeno un rettangolo inscritto in \(\gamma\), simile al rettangolo \(R\).
Ovvero non solo c’è un quadrato inscritto, ma ci sono rettangoli di tutte le forme (o meglio di tutte le proporzioni). Non male davvero, come salto in avanti.
Purtroppo la congettura per una curva chiusa semplice qualsiasi rimane ancora aperta.
