I mondi paralleli non possono essere troppo diversi gli uni dagli altri: Alessandro Vannini, recentemente dottorato all’ Università dell’ Aquila, ci racconta come secondo un recente articolo apparso nell’Asian Journal of Mathematics.
Nel recente articolo “AN ε-REGULARITY THEOREM FOR LINE BUNDLE MEAN CURVATURE FLOW”, pubblicato su Asian Journal of Mathematics, gli autori, X.Han (Department of Mathematical Sciences, Tsinghua University, Beijing, China) e H. Yamamoto (Department of Mathematics, Faculty of Pure and Applied Science, University of Tsukuba, Ibaraki, Japan), hanno presentato una tecnica che, sotto delle ragionevoli ipotesi, garantisce l’esistenza di cosiddette metriche Hermitiane di Yang-Mills deformate (dHYM in breve). La ricerca di metriche con proprietà speciali costituisce uno dei filoni di ricerca più affascinanti e stimolanti della geometria differenziale e le tecniche con le quali è possibile affrontarli spaziano dall’analisi geometrica alla topologia e alla geometria algebrica (e molto altro ancora).

Figura 1 – Varietà differenziabili
Ma cosa è una metrica? E perché sono importanti queste studiate nell’ articolo? Per capirlo dobbiamo fare un piccolo ripasso del legame che la geometria differenziale, sin dalla sua nascita, ha intrecciato con la fisica. Gli oggetti geometrici con cui solitamente un geometra differenziale lavora sono le cosiddette varietà differenziabili (Figura 1). Per varietà si intende, idealmente, una qualsiasi forma geometrica ci possa venire in mente, mentre l’aggettivo “differenziabile” (o anche “liscia”) vuole specificare che la forma in questione non possa presentare estremità appuntite o auto intersezioni, e che sia possibile applicare la potente macchina del calcolo differenziale e integrale. Pertanto, quando si incontra il termine “varietà” non è sbagliato avere in mente l’immagine di una sfera o di una retta ma bisogna evitare figure come un cono o la curva che tracciamo per scrivere un “8”. Per poter fare effettivamente della geometria sulle varietà abbiamo bisogno di poter misurare angoli, calcolare la distanza tra due punti oppure calcolare aree, volumi e così via. L’oggetto matematico che rende possibile tutto ciò è il concetto di “metrica Riemanniana” (dal matematico G.F.B. Riemann, allievo di Gauss e uno dei padri fondatori della geometria differenziale) o semplicemente metrica. Questa contiene tutta l’informazione necessaria a studiare le proprietà geometriche del nostro spazio e tramite essa è possibile definire concetti più avanzati come quello di curvatura o di geodetica.
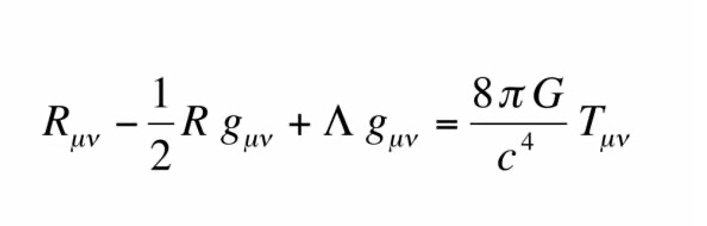
Figura 2- Equazione di campo di Einstein
Una stessa varietà può ammettere metriche diverse e di conseguenza può avere proprietà geometriche molto differenti a seconda della metrica scelta. Ad esempio, nella famosa equazione di Einstein della relatività generale (Figura 2), il termine incognito è proprio una metrica! Essa ci ha insegnato che il modo in cui il nostro spazio-tempo cambia la sua geometria è legato alla presenza di massa e questo è dovuto proprio al fatto che l’equazione di Einstein mette in relazione una metrica, e la sua curvatura, con il contenuto di energia legato alla presenza di corpi massivi. Un problema tipico è infatti quello di impostare un’equazione che coinvolga una metrica e delle condizioni che essa deve soddisfare, solitamente motivate da argomenti fisici come l’ottimizzazione (minimizzazione o massimizzazione) di certe quantità. Una volta ottenuta tale equazione non è detto però che essa ammetta una soluzione, e qualora esistesse possiamo comunque interrogarci sulla sua unicità. Infatti, risolvere un’equazione del genere, come ad esempio quella di Einstein, equivale a risolvere un sistema di equazioni alle derivate parziali (EDP), compito tutt’altro che facile. Ed è qui che entra in gioco l’analisi geometrica che tra i suoi vari ambiti tratta proprio lo studio di equazioni alle derivate parziali che nascono dalla geometria. Prima di arrivare però a trattare l’equazione dHYM, citata al principio, cerchiamo di capire qual è la sua versione iniziale, ovvero “non deformata”. Per cominciare bisogna per un momento tornare alle nostre varietà differenziabili e sottolineare che, quando ci si riferisce a esse, solitamente si sta dando per scontato che esse siano reali, ovvero che il modello geometrico locale con cui intendiamo descriverle, è basato sullo spazio euclideo \(\mathbb{R}^n\), prodotto cartesiano di n copie della retta dei numeri reali. Con questo intendiamo dire che, se volessimo guardare con una potente lente d’ingrandimento una varietà bidimensionale (come una sfera), questa localmente, cioè, fissando un punto e soffermandoci lì intorno, ci sembrerà essere indistinguibile da una porzione di piano cartesiano. Nulla però ci vieta di modificare questo concetto e prendere come modello locale, invece che uno spazio euclideo reale, uno spazio euclideo complesso \(\mathbb{C}^n\), prodotto cartesiano di n copie del piano complesso. Una delle immediate conseguenze è il fatto che la dimensione degli oggetti trattati raddoppia! Infatti, siccome l’insieme dei numeri complessi \(\mathbb{C}\) si può identificare al piano cartesiano \(\mathbb{R}^2\), considerare in geometria complessa una curva (che è un ente uno-dimensionale) corrisponde a considerare una superficie in geometria reale. Tutti i concetti finora incontrati hanno la loro estensione nei numeri complessi e in particolare, l’analogo di una metrica Riemanniana, prende il nome di metrica Hermitiana (dal matematico C. Hermite).

Figura 3- Lagrangiana del modello standard
Per poter invece comprendere il significato di “Yang-Mills” bisogna fare un rapido salto nel mondo della teoria quantistica dei campi (Figura 3). Quando in fisica matematica si cerca di descrivere la dinamica di un corpo o di un sistema, un tipico approccio è quello di scrivere le corrispettive equazioni di Eulero-Lagrange che generalizzano il secondo principio di Newton. Per poter ricavare tali equazioni si scrive una funzione (anzi un funzionale d’azione) i cui punti critici corrispondono proprio alle soluzioni delle equazioni di Eulero-Lagrange. Se vogliamo passare alla dinamica di particelle quantistiche, bisogna ricorrere alla teoria quantistica dei campi e, per poter incorporare nella trattazione anche le simmetrie previste dal modello standard, la tecnica utilizzata passa per la definizione del cosiddetto funzionale di Yang-Mills. Le equazioni ottenute dallo studio dei punti critici di questo funzionale possono essere impiegate per ricavare delle metriche che, per l’appunto, prenderanno il nome di metriche di Yang-Mills [1 ]Ad essere precisi gli oggetti geometrici che vengono utilizzati in teoria di gauge (la versione matematica della teoria quantistica dei campi) sono derivate covarianti associate a connessioni su fibrati. Tuttavia, dei famosi risultati teorici come la corrispondenza di Kobayashi-Hitchin o di Donaldson-Uhlenbeck-Yau permettono di convertire un problema con le connessioni in un problema che coinvolge le metriche.. Questo perché c’è un legame matematico molto profondo tra la descrizione, anche solamente classica, delle teorie di campo, come quello elettromagnetico, e il moderno linguaggio della geometria differenziale (ma questa è una bellissima storia che siamo costretti a rimandare a un’altra occasione!). Finalmente possiamo parlare dell’origine dell’equazione dHYM e questo ci riporta invece a un altro argomento di fisica teorica: la teoria delle stringhe (che abbiamo già trattato nella recensione del libro “La forma dello spazio profondo” qui).
Figura 4- Simmetria speculare per varietà di Calabi-Yau
Sappiamo infatti che esistono vari modelli di teoria delle stringhe e alcuni di essi sono connessi da alcune dualità. Ciò significa che nonostante due modelli siano profondamente diversi, ci si è accorti che fenomeni esclusivi di un primo modello corrispondono a fenomeni esclusivi dell’altro. Questa relazione ha una sua interpretazione squisitamente matematica che va sotto il nome di “simmetria speculare” (“mirror symmetry” dall’inglese) e prevede che due branche della geometria, apparentemente scollegate, la geometria complessa da un lato, e la geometria simplettica dall’altro siano in realtà uno lo specchio dell’altro, come due mondi paralleli (Figura 4). Abbiamo già incontrato la geometria complessa (quella modellata su \(\mathbb{C}^n)\), mentre invece la geometria simplettica è una branca della geometria differenziale che studia le varietà (simplettiche) che a loro volta sono modellate sullo spazio delle fasi della fisica matematica. Per i più navigati che hanno avuto modo di incontrare già meccanica razionale o meccanica quantistica, ciò significa che su una varietà simplettica vi è una nozione di coordinate coniugate “posizione” e “momento”. Uno degli oggetti tipici studiati in geometria simplettica (Figura 5), sono le cosiddette sottovarietà Lagrangiane speciali e, secondo il dizionario fornito dalla simmetria speculare, queste sono direttamente collegate all’esistenza delle nostre fatidiche metriche dHYM che vivono nel mondo della geometria complessa.

Figura 5 – Rappresentazione schematica per il calcolo dell’omologia di Floer, utilizzata in geometria simplettica
Qui, infatti, il “deformate” semplicemente sta a indicare che le equazioni che vengono ricavate dalla conversione “attraverso lo specchio” contengono una piccola modifica rispetto alle già note HYM ed hanno quest’ultime come caso particolare. L’importanza del risultato ottenuto dai due ricercatori è dunque duplice: da una parte hanno reso possibile costruire questo genere di metriche, estremamente complicate, rimanendo nel mondo complesso e soprattutto senza passare per lo “specchio”, e, dall’altra, le innovative tecniche di analisi geometrica utilizzate potranno avere delle ricadute costruttive che potranno aiutare a comprendere e ad analizzare meglio la teoria delle EDP e dei flussi geometrici associati.
Alessandro Vannini
Note e riferimenti
| ⇧1 | Ad essere precisi gli oggetti geometrici che vengono utilizzati in teoria di gauge (la versione matematica della teoria quantistica dei campi) sono derivate covarianti associate a connessioni su fibrati. Tuttavia, dei famosi risultati teorici come la corrispondenza di Kobayashi-Hitchin o di Donaldson-Uhlenbeck-Yau permettono di convertire un problema con le connessioni in un problema che coinvolge le metriche. |
|---|












Trackback/Pingback