“Curioso,” convenne Reg. “A me certamente non è mai capitato di imbattermi in un’operazione matematica irreversibile che coinvolgesse un divano. Potrebbe essere un nuovo campo di studi. Hai provato a parlarne con un esperto di geometria spaziale?” “Ho fatto di meglio. Ho chiamato il figlio di un vicino che una volta era capace di risolvere il cubo di Rubik in diciassette secondi. Si è seduto su un gradino e l’ha guardato fisso per più di un’ora, poi ha decretato che era bloccato irrimediabilmente. (D.Adams, Dirk Gently, Agenzia Investigativa Olistica)
Apparso originariamente il 2 gennaio 2017
di Nicola Ciccoli
Sarà capitato a molti: una tranquilla Domenica mattina di ozio, l’intenzione di mettere ordine in casa e così, dopo un’ora ci si ritrova sudati e perplessi a muovere tutti i mobili in un improvvisato trasloco interno. “Quel divano starebbe benissimo nello studio”, un’idea apparentemente perfetta fino a quando, dopo aver faticato per spostare il pesantissimo divano ci si ritrova incastrati a metà corridoio a chiedersi come fare per permettere al divano di superare quella piega del corridoio che sembra irrimediabilmente bloccarlo.
Nella domenica di ozio ci si ritrova a contemplare la possibilità di smontare il divano fino alla più piccola vite e rimontarlo al di là dell’ostacolo. Il matematico Leo Moser, invece, nel 1966 ([3]) formalizzò il seguente problema: dato un corridoio largo 1 metro, con una curva ad angolo retto, qual è l’area massima (e la forma che la realizza) di un “divano” rigido capace di superare quella piega ed essere portato da una parte all’altra del corridoio.Nasceva così il “sofa problem” e probabilmente nessuno avrebbe immaginato che a cinquant’anni di distanza la soluzione ancora ci sfugga. È immediato verificare che con semplice traslazioni un divano quadrato di lato 1 metro passerà per il corridoio. Leggermente più complicato verificare che anche un divano a semicerchio di raggio 1 (e area, quindi, circa di 1.57), con una combinazione di traslazioni e rotazioni supererà il gomito del corridoio.
Una soluzione interessante al problema è stata proposta da Hammersley [2] in un articolo che, come evidente dal titolo, è centrato su ben altro problema, forse il tipico problema di un matematico reale che sposta divani la domenica mattina. Se vi è capitato di restare incastrati a metà corridoio con un divano reale avete certamente contemplato l’idea di armarvi di una sega e tagliare un tassello nell’area centrale del divano. Seguendo questa intuizione e qualche semplice conto di Analisi, in quest’articolo si descriveva quello che poi sarebbe diventato famoso come il divano di Hammerseley, un profilo descritto da segmenti lineari e archi di cerchio che delimitano una figura di area π/2+2/π∼2,20 che si congetturò essere ottimale. Nello stesso articolo si dimostrava come l’area massima di un tale divano non poteva superare il valore di 2√2∼2,828.

Il divano di Hammerseley
L’ipotesi che il divano di Hammerseley potesse essere ottimale ha resistito a lungo, sino a che Gerver [1] ha fatto notare che a partire da quella forma era possibile introdurre piccole modifiche e ottenere un aumento di area. Nel suo lavoro del 1992 ha trovato un profilo di divano descritto da 15 distinti segmenti di curva combinati tra di loro, con un’area di circa 2,22, soluzione che a tutt’oggi resta la migliore possibile del problema del divano, pur non essendo molto esplicita: le formule che descrivono il profilo del parametro dipendono da alcuni parametri numerici che devono verificare un complicato sistema di equazioni non lineari le cui soluzioni non sono esprimibili in forma chiusa.
Recentemente il problema ha avuto un ritorno di interesse quando Romik ha dato una soluzione in forma chiusa per un problema simile: il problema del divano ambidestro, in cui si richiede al divano di percorrere un corridoio che abbia due curve ad angolo retto nelle due direzioni opposte. Adattando le tecniche di Gerver a questo problema, Romik [4] ha costruito una soluzione del problema del divano ambidestro data da una curva profilo descritta da 18 distinti segmenti di curva, che perfeziona una soluzione precedente ottenuta usando tecniche di calcolo numerico; in questa soluzione ciascun segmento si esprime in forma chiusa come curva algebrica di sesto grado.
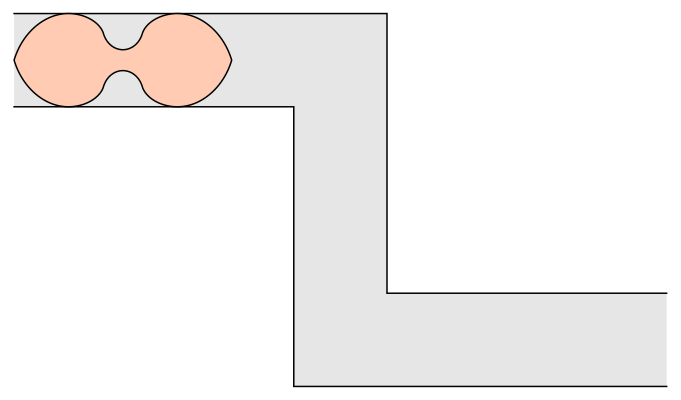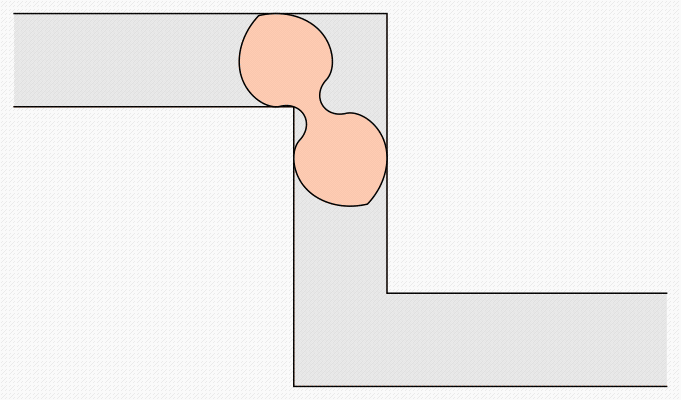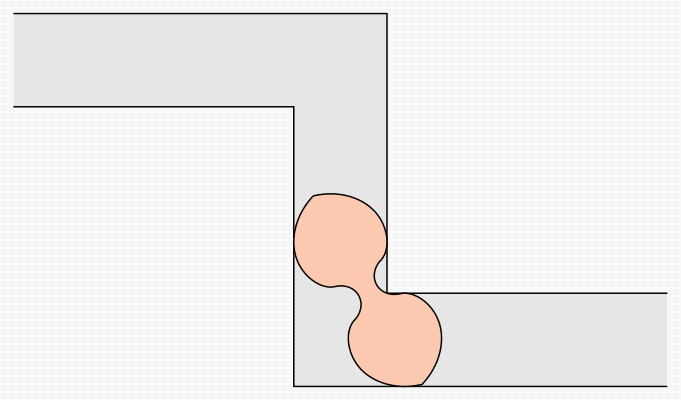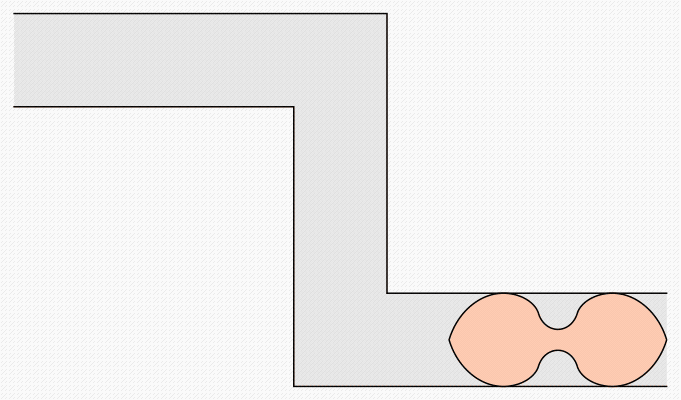
Il divano di Romik
Anche la soluzione di questo problema non è stata dimostrata essere la migliore possibile, anche se costituisce un miglioramento delle soluzioni precedenti. E’ d’altra parte stato dimostrato, proprio da Gerver, che una soluzione ottima esiste. In attesa che i matematici riescano a risolvere questo problema, aperto da cinquant’anni, i nostri traslochi continueranno a porci problemi apparentemente troppo difficili.
Bigliografia
- Gerver J. L., On moving a sofa around a corner, Geom. Ded. 42(1992) 267-283, doi:10.1007/BF02414066.
- Hammersley, J. M., On the enfeeblement of mathematical skills by “Modem Mathematics” and by similar soft intellectual trash in schools and universities, Bull. Inst. Math. Appl. 4 (1968), 66-85.
- L. Moser , Moving furniture through the hallways, Siam Review (1966).
- D. Romik, Differential equations and exact solutions in the moving sofa problem, arXiv:1606.08111.
- Wagner, N. R., “The Sofa Problem”, American Math Monthly 83 (1976) 188-189.