Perito elettorale? Ma esiste? Sembrerebbe di si! Almeno fra qualche anno, quando la scuola di formazione per periti elettorali fondata da Moon Duchin, professoressa di Matematica alla Tufts University, sarà a regime (il primo corso della durata di 5 giorni, inizierà il prossimo Agosto). Sorprendentemente, il perito sarà un matematico. Meglio ancora se un geometra. Suo sarà il compito di aiutare i giudici nello stabilire se particolari risultati elettorali non siano soggetti alla pratica costituzionalmente viziosa del cosiddetto gerrymandering. Abbiamo appreso la  notizia qui e Nicola Apollonio dell’IAC-CNR l’ha commentata per MaddMaths!

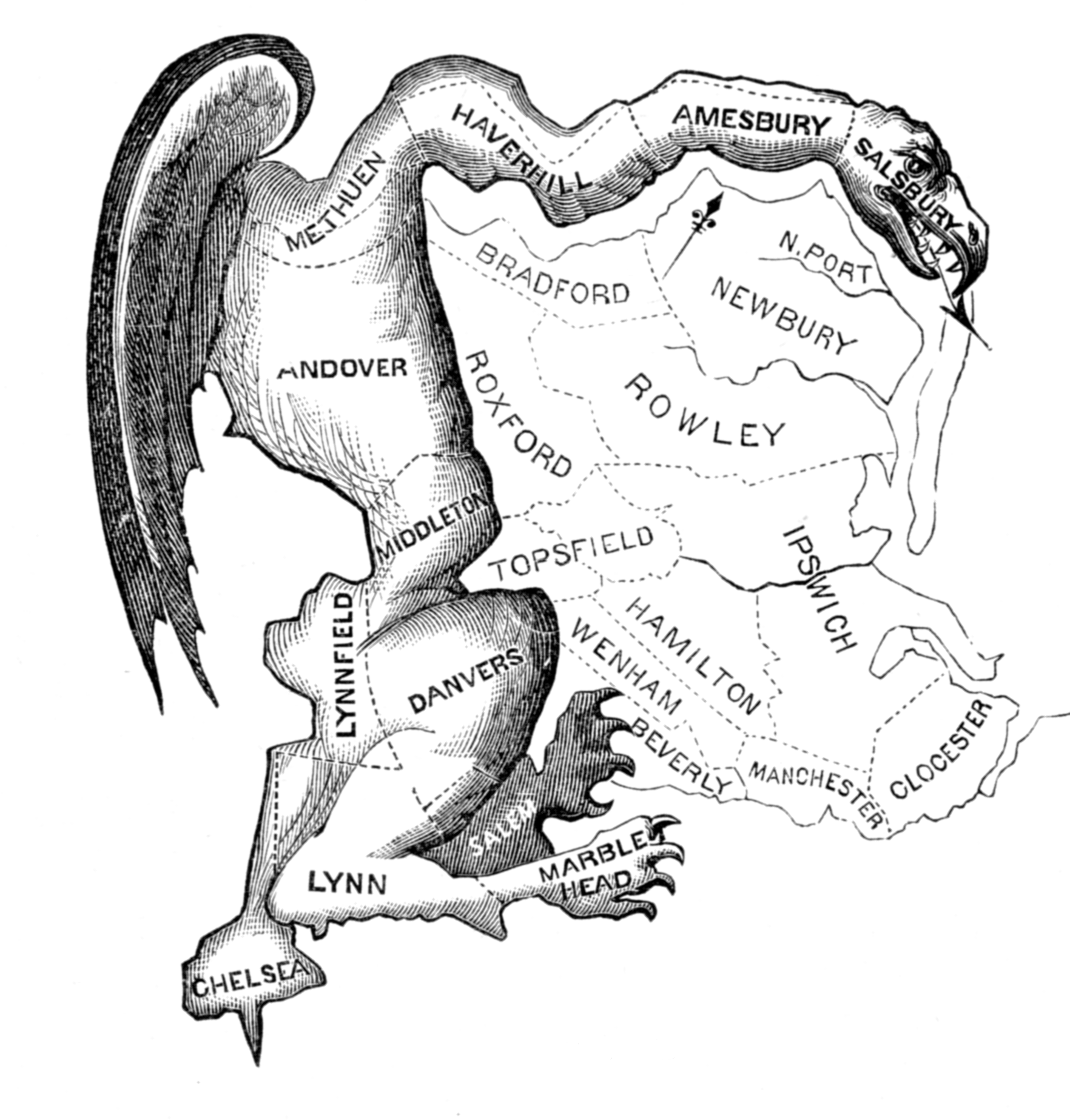
Il termine gerrymandering (che potremmo tradurre con “salamandrando alla maniera di Gerry”) si forma per sincrasi del nome del senatore Elbridge Gerry e di salamander. Esso fu coniato nel 1812 dagli avversari politici del senatore per denunciare il fatto che quest’ultimo avesse ridisegnato i confini del proprio collegio al fine di includere gruppi di elettori favorevoli, collocati all’esterno del collegio originario, ed escludere gruppi elettorali ostili collocati all’interno.

L’effetto plastico che ne conseguì fu quello di un collegio elettorale dai confini particolarmente tortuosi in cui gli avversari scorsero il bordo di una salamandra (vedi figura di copertina).    

I sistemi elettorali più fragili al gerrymandering sono quelli maggioritari con collegi uninominali in cui l’elettorato sia bipolare (proprio come nel caso degli Stati Uniti). Non a caso la scuola di formazione nasce anche per lo stimolo di una sentenza della Suprema Corte che assoggetta modifiche alle leggi elettorali di certi stati all’autorizzazione federale. L’eventuale ridisegno dei collegi elettorali in quegli stati dovrà dunque essere approvato dalla corte.

Un sistema maggioritario con collegi uninominali per l’elezione di un’assemblea, nell’ipotesi che concorrano due soli partiti, funziona così: il territorio è diviso in collegi elettorali; in ciascun collegio è in palio un seggio dell’assemblea; il seggio è assegnato al candidato che ottiene la metà più uno dei voti del collegio (nella pratica si è un po’ più cauti e si assume che lo scarto consista di una percentuale ragionevolmente rassicurante dei votanti); l’assemblea è infine composta dai candidati che hanno ottenuto un seggio; il partito che ha la maggioranza in assemblea è quello che detiene la maggioranza dei seggi. Un modello fedele di sistema maggioritario con collegi uninominali per un territorio il cui elettorato sia bipolare consiste dunque di: un territorio, rappresentato da una superficie (possiamo pensare ad una porzione di piano, così come appare su una qualsiasi carta geografica);  un insieme  finito di punti colorati di blu o di rosso  che rappresentino gli elettori (la scelta dei colori non autorizzi alcuna induzione: il rosso e il blu sono i colori più comunemente usati nei problemi di equipartizione di misure in geometria discreta); una partizione del territorio (in insiemi con interno disgiunto) che rappresenti  la distrettizzazione elettorale. I risultati di una competizione elettorale su un territorio rettangolare con 12 elettori di cui 6 blu e 6 rossi potrebbero apparire dunque così:

Come si vede, un medesimo risultato elettorale (distribuzione di punti rossi e blu nel territorio) conduce ad esiti completamente diversi nella distribuzione dei seggi a seconda della partizione scelta. La “simmetria” delle precedenti configurazioni non ci tragga inganno: geometria permettendo, se conoscessimo “a priori” la distribuzione dei punti (p.es. analizzando serie storiche elettorali o commissionando sondaggi) e potessimo praticare il gerrymandering più libero e sfrenato, riusciremmo  a favorire il più possibile anche il partito che ci aspettiamo  prenda in assoluto meno voti. Infatti, una volta fissati il numero di collegi e la bicolorazione, per vincere nel maggior numero di collegi conviene vincere in ciascun collegio con il minimo scarto possibile: i voti che eccedono la metà più uno sono dunque voti sprecati (come sono sprecati i voti dei collegi in cui si perde). Per esempio, se il territorio contiene 18 punti rossi e 30 blu (distribuiti come nella figura seguente)

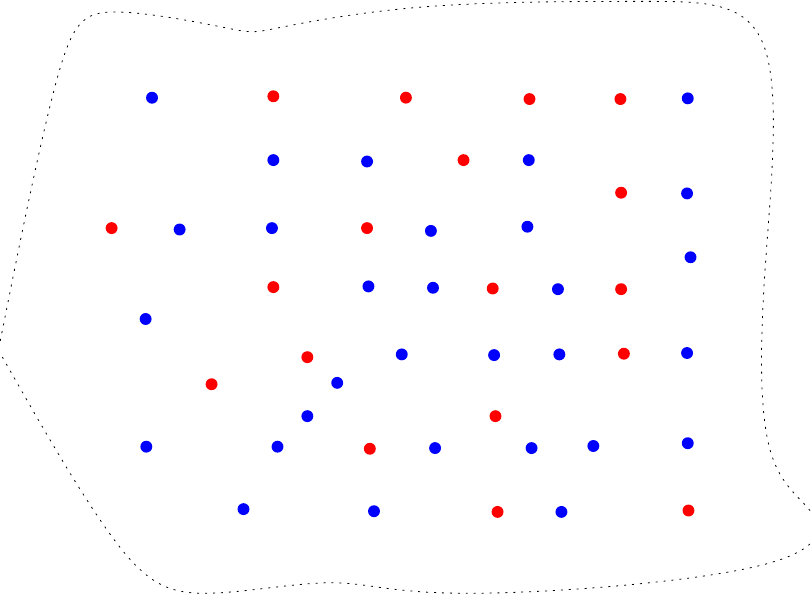
e i collegi sono 5, allora,  geometria permettendo, potremmo formare i collegi in questo modo: 3 collegi con 5 punti rossi e 4 blu ciascuno, 1 collegio contenente solo punti blu e un ultimo collegio più grande contenente 9 punti blu e 3 rossi. Assicureremmo così la maggioranza dei collegi ai punti rossi che sono poco più della metà del totale dei punti blu. Già, ma se questo non è possibile? Così facendo potremmo formare infatti collegi sconnessi (ciò che permette l’aritmetica potrebbe non essere permesso dalla geometria). Beh, ma se la geometria chiede solo che i collegi siano connessi, non è poi così difficile accontentarla:

La condizione di “connessione” non previene dunque il gerrymandering estremo. La geometria deve essere senz’altro più severa! Ciò accade imponendo ai distretti di essere compatti. Benché la nozione di compattezza dei collegi (che non va confusa con l’omonima nozione topologica) sia una nozione ancora vaga e imprecisa dal punto di vista matematico essa è, secondo la Duchin,  riconosciuta implicitamente nelle costituzioni di molti stati federati. Parlando a spanne: un collegio è compatto se ha un buon rapporto di forma e appare spazialmente ben distribuito. Benché, come detto, una definizione precisa non esista, esistono tuttavia indici di compattezza di un collegio (e dunque di una partizione) [Au]. Per esempio, guardando al rapporto di forma, un collegio è compatto se è una soluzione soddisfacente al Problema di Didone: recintare il più grande pezzo di terra che si può recintare con una corda di lunghezza fissata (sulla terra così recintata Didone riusci ad edificare Cartagine). Secondo questa nozione di compattezza, a parità di perimetro sono più compatti i collegi più estesi o, equivalentemente, quelli per i quali più alto risulta l’indice di Polsby-Popper  definito come il rapporto \(\frac{4\pi A}{P^2}\), dove \(A\) e \(P\) sono l’area e il perimetro del collegio. In virtù della disuguaglianza isoperimetrica, l’indice non supera 1 e raggiunge tale valore massimo quando il collegio è un cerchio. Altri indici basati sul confronto di aree sono variazioni sul tema: rapporto tra l’area del collegio e quella del cerchio che la circoscrive (Reock ratio) o il convex-hull ratio definito come il rapporto tra l’area del collegio e l’area del più piccolo insieme convesso che lo contiene. Si noti che in quest’ultimo caso, sono considerati massimamente compatti i collegi convessi. Un indice diverso, noto come indice di bizarreness, calcola quanto mediamente si allunga la strada più breve tra due punti del collegio utilizzando solo “cammini” del collegio piuttosto che tutti i “cammini” del territorio. Tanto più si allunga, tanto più la metrica “intrinseca” è distorta rispetto a quella del territorio, tanto più il collegio presenta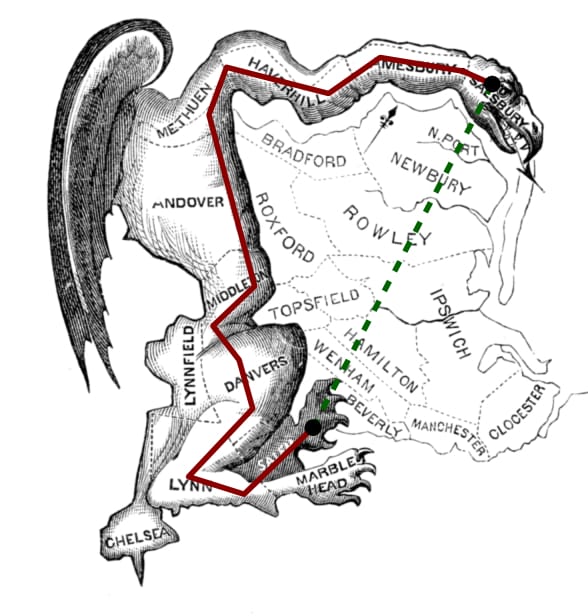 delle “bizzarrie geometriche” eventualmente sintomatiche di avvenute manipolazioni (come nel caso della “salamandra bizzarra” qui accanto).

Infine, un indice molto amato dai costituzionalisti  perché ritenuto di facile comprensione e direttamente informativo (a quanto dice la Duchin), è il cosiddetto efficiency-gap. Si tratta di un indice che, fissata la partizione, confronta l’efficienza dei due partiti nel trasformare i propri voti in seggi calcolando le percentuali dei voti sprecati  (nel senso discusso più sopra). Nel caso dell’esempio, la percentuale dei voti sprecati dai blu è del 60% (18 voti su 30) mentre i rossi, molto più efficientemente, sprecano poco meno del 17% dei voti (3 voti su 18).  Un’alta discrepanza tra le percentuali è ritenuta sospetta.

La combinatoria fornisce molti strumenti per costruire esempi molto strutturati di gerrymandering estremo. Tuttavia il compito più  arduo rimane quello di riconoscere il gerrymandering. Facciamolo vedere “spremendo” il  bel Equitable Subdivision Theorem della geometria discreta [KaKa] che enunciamo in una forma leggermente più debole dell’originale.

Teorema (dell’equipartizione). Siano \(R\) e \(B\) sottoinsiemi finiti e disgiunti del piano tali che i punti di \(R\cup B\) siano a tre a tre non allineati. Siano poi \(r\), \(b\) e \(p\) interi tali che \(r\geq 1\), \(b\geq 1\) e \(p\geq 2\). Se \(R\) contiene \(pr\) punti rossi e \(B\) contiene \(pb\) punti blu, allora esiste una partizione del piano in \(p\) insiemi convessi ciascuno dei quali contiene esattamente \(r\) punti rossi e \(b\) punti blu.

Il teorema precedente appartiene ad una classe di risultati che dimostrano costruttivamente l’esistenza di partizioni massimamente bilanciate di arbitrari sottoinsiemi finiti e bicolorati del piano. Per esempio, per \(p=2\), il teorema implica che i punti possono essere separati in due insiemi ciascuno dei quali contiene esattamente la metà dei punti rossi e la metà dei punti blu. Ne esistono versioni più raffinate tuttavia vogliamo dare solo un’idea di come si possa forzare una sorta di “eterogenesi dei fini” per produrre partizioni sostanzialmente inique. Infatti, si ponga \(b=r+1\) nel teorema, sicché \(bp-rp=p\). Il teorema garantisce (con una dimostrazione costruttiva) l’esistenza di una partizione in cui, data la distribuzione dei voti, i blu vincono in tutti i collegi . Si potrebbe obiettare che non vi sarebbe nulla di ingiusto: in fin dei conti i blu sono la maggioranza.  D’altra parte, siccome il numero dei collegi è pari al numero di seggi di un’assemblea, nei casi reali \(p\) è dell’ordine al più delle centinaia mentre \(rp\) è dell’ordine almeno dei milioni (spesso decine di milioni). Si capisce dunque come differenze anche solo di poche centinaia di voti su milioni di votanti possano causare vittorie clamorose. Peggio ancora: la partizione asserita nel teorema è una partizione in insiemi convessi (quindi non bizzarri rispetto alla distanza euclidea) e massimamente compatti (per il convex-hull ratio). Inoltre, utilizzando estensioni più raffinate del teorema di equipartizione, si può provare ad ingannare anche l’ efficiency-gap che, in questo caso, è l’unico in grado di rilevare (ove ce ne fosse bisogno) la palese iniquità della partizione (i rossi sprecano il 100% dei voti mentre i blu non sprecano alcun voto).  In conclusione ha proprio ragione la Professoressa Duchin: combattere il gerrymandering è “roba da matematici” tanto più che i gerrymanderer probabilmente lo sono già.

Nicola Apollonio
Istituto per le Applicazioni del Calcolo – Consiglio Nazionale delle Ricerche

RIFERIMENTI

[Au] D. Austin, AMS Feature Column, “Congressional Redistricting and Gerrymandering“.

[KaKa] A. Kaneko, M. Kano, Discrete geometry on red and blue points in the plane – A survey. Discrete and Computational Geometry, The Goodman-Pollack Festschrift, Algorithms and Combinatorics, vol. 25, Springer-Verlag (2003), pp. 551–570.