Gabriel Popkin su Quanta Magazine parla di “buttare via le equazioni” (Throw out the equations) nello studio delle scienze naturali. Abbiamo chiesto a Hykel Hosni e Angelo Vulpiani di scrivere una riflessione per il nostro sito su questo drastico punto di vista.

George Sugihara[/caption]

L’articolo con cui, ormai quasi dieci anni fa Chris Anderson sosteneva la fine della teoria viene subito alla mente. Bene, non soltanto quest’idea non è stata superata, ma addirittura sembra essere stata assimilata da molti componenti della comunità scientifica, e con un certo entusiasmo anche da chi si occupa delle politiche della ricerca e ne indirizza i finanziamenti. È dunque opportuno soffermarci sulla questione con spirito critico e ribadire un messaggio duplice. Da una parte non v’è alcun dubbio che le recenti tecniche per la raccolta e l’analisi (algoritmica) di grandi varietà e quantità di dati costituiscano una sfida scientificamente molto interessante e di elevato impatto potenziale in tutti gli strati della società. D’altra parte però, è necessario non cedere a facili entusiasmi, e in particolare alla tentazione di pensare che la soluzione a tutti i problemi dipenda dallo sviluppo di questa interessante e sofisticata tecnologia, che alcuni descrivono come foriera di un’imminente rivoluzione epocale, quella del “quarto paradigma” che andrebbe di fatto a sostituirsi al metodo sperimentale, quello teorico e quello computazionale. A questo proposito Popkin scrive addirittura che Sugihara e gli altri stanno ora iniziando ad applicare il metodo oltre l’ecologia, e in particolare in finanza, nelle neuroscienze e perfino in genetica.

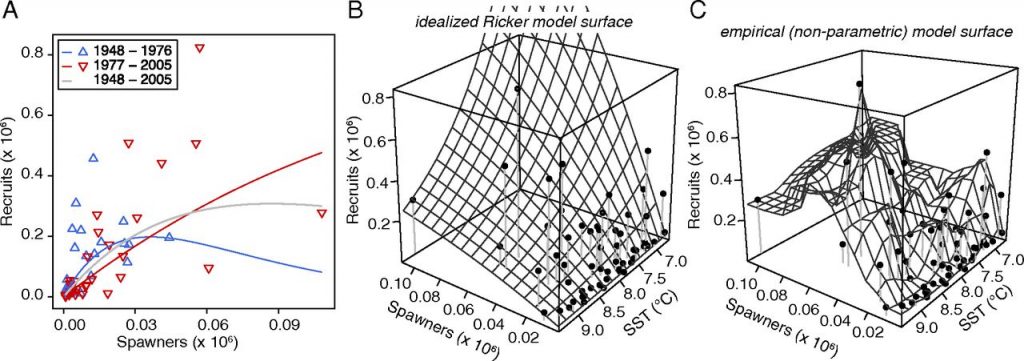
Output di modello per i modelli di Ricker, Ricker esteso, e EDM multivariato (ripreso da PNAS March 31, 2015 vol. 112 no. 13 E1569-E1576 )

Partiamo dall’ovvio: i problemi scientifici non sono tutti uguali. Dal punto di vista della metodologia predittiva, il caso più semplice è quello della fisica classica. Qui si ha un modo di procedere abbastanza chiaro: una volta capite le forze in gioco si possono scrivere delle equazioni differenziali che magari sono di difficile soluzione, ma che comunque ci permettono sempre di ottenere qualche risultato affidabile, esempio con analisi qualitativa oppure uno studio numerico. Decisamente più complicato è il caso dei sistemi non deterministici, che oltre a certe aree della fisica, riguardano le scienze della vita, incluse la biologia e la medicina. In questi ambiti non si ha niente di simile alle leggi di Newton o di Maxwell e quindi la derivazione di un’equazione non può che nascere da un’intuizione profonda e per nulla scontata, magari suggerita da osservazioni empiriche. Un esempio famoso (e istruttivo) è costituito dalle equazioni di Lotka-Volterra: \[{dx \over dt}= – a x +b x y \,\,\,\,\, , \,\,\,\, {dy \over dt}= c y – d x y \ \ (1)\] ove \(x\) e \(y\) sono rispettivamente il numero di predatori e prede, e le costanti \(a, b, c\) e \(d\) sono positive. Questo modello che descrive, almeno a livello qualitativo, un semplice sistema ecologico, è stato introdotto notando l’analogia tra l’interazione preda/predatore e l’urto di due atomi nella teoria cinetica.

Ancora più ricco di complicazioni metodologiche è il caso delle scienze sociali, e in particolare dell’economia matematica. In questo ambito, ogni modello teorico contiene due aspetti distinti. Il primo si occupa di identificare le condizioni desiderabili che gli individui devono soddisfare secondo le prescrizioni del modello. Un certo numero di condizioni (assiomi) definiscono cosa si debba intendere in quel contesto, per esempio, per “scelta razionale” e la teoria si sviluppa traendo le conclusioni (teoremi) che seguono logicamente da quelle ipotesi. Il secondo ambito si occupa invece di raccogliere i dati sul comportamento reale degli individui per elaborare previsioni il più accurate possibili. Accade spesso che le osservazioni siano in conflitto con le prescrizioni della teoria, ma questo non porta (quasi mai) ad abbandonare il modello. Non si tratta (sempre) di voler difendere ostinatamente teorie sbagliate, ma del fatto che una teoria può dare prescrizioni utili anche quando sia descrittivamente inaccurata. La situazione è simile a quella per cui, correggendo gli esami degli studenti, i matematici di tutto il mondo tendono a non considerare refutata, e quindi da abbandonare, la teoria della probabilità. Nell’ambito degli esami universitari, questa non è infatti da considerarsi una previsione su come ragioneranno gli studenti, ma stabilisce i canoni di come dovrebbero ragionare. Ecco, più in generale, una differenza metodologica profonda che intercorre tra i modelli predittivi nelle scienze naturali e sociali: un individuo può sbagliarsi e può usare la parte prescrittiva della teoria per correggere i propri errori. E a questo si aggiunga il fatto che i meccanismi che governano il comportamento umano, se esistono, sono il risultato di un groviglio di fattori che non è affatto realistico pensare di poter catturare nelle “leggi del comportamento”. Si tratta di differenze metodologiche evidenti che devono metterci in guardia da qualsiasi promessa di approccio universale ai modelli predittivi: non c’è alcuna ragione per credere che se i dati crudi sono sufficienti a formulare previsioni accurate relativamente a certi ecosistemi, le stesse tecniche analitiche, o di empirical dynamical modelling, ci permettano di formulare previsioni altrettanto accurate in ambiti completamente diversi che spaziano dalla finanza alla biologia. Ma c’è di più: i dati crudi non sono sufficienti nemmeno nell’ambito metodologicamente più semplice, quello dei sistemi dinamici finiti.

Torniamo alle equazioni di Lotka-Volterra, che l’articolo commentato da Popkin vedrebbe, presumibilmente, soppiantate dalle serie storiche dei dati dell’ecosistema di riferimento. Iniziamo osservando che, in un certo senso, non si tratta di un’idea del tutto bislacca. In un ecosistema complesso con molti predatori e prede, fenomeni di simbiosi e parassitismo, la (1) è rimpiazzata da un’ equazione differenziale costruita facendo necessariamente appello all’intuizione e ai dati ottenuti dalle osservazioni. Tipicamente la forma funzionale è suggerita dal tipo di interazione tra ogni coppia di specie, cioè preda-predatore, simbiosi o parassitismo, mentre i valori dei parametri sono ricavati dai dati. Possiamo ottenere una soluzione più neutrale e sistematica? Dopo tutto, si potrebbe obiettare, l’intuizione non è certo oggettiva, e non tutti hanno le capacità creative di Volterra! È possibile, in altre parole, trovare un metodo per generare le equazioni a partire dai dati e senza l’uso di analogie, o addirittura liberarsi del tutto delle equazioni e, usando solo le osservazioni capire il comportamento del sistema? Nel caso delle previsioni, in parte la risposta è positiva.

Consideriamo la situazione più favorevole in cui sappiamo che il fenomeno è descritto da un vettore \({\bf x}(t)\) di cui conosciamo la storia passata \({\bf x}_1, {\bf x}_2, … , {\bf x}_M\), ove \({\bf x}_k={\bf x}(k \Delta t)\), e \(\Delta t\) è il tempo di campionamento. Per fare una previsione del futuro si cerca nel passato una situazione “vicina“ a quella di oggi, se la si trova al giorno \(k\) allora è sensato assumere che domani il sistema sarà “vicino” al giorno \(k+1\). In termini un più formali si cerca un analogo, ovvero un vettore \({\bf x}_k\) con \(k<M\) “abbastanza vicino“, cioè tale che \(|{\bf x}_k- {\bf x}_M|< \epsilon\) (ove \(\epsilon\) indica il grado di accuratezza desiderato), una volta trovato si “predice” il futuro ai tempi \(M + n > M\) , semplicemente assumendo per \({\bf x}_{M+n}\) lo stato \({\bf x}_{k+n}\). Ovviamente se il sistema è caotico l’incertezza del metodo cresce velocemente con \(n\), ma questo è un problema non eliminabile.

Molto spesso non si conoscono le variabili che descrivono il fenomeno e se si ha a disposizione solo la serie temporale di una certa quantità \( u_1, u_2, …, u_M\), come risalire alle “variabili giuste”? Questo è il problema della ricostruzione dello spazio dell fasi, risolto negli anni 80 da Floris Takens: se il sistema è deterministico e \(M\) è abbastanza grande è possibile ricostruire lo spazio delle fasi con il vettore \({\bf y}^{(d)}\) costruito con il metodo dei ritardi: \[{\bf y}^{(d)}_j= (u_j,u_{j-1}, … , u_{j-d+1}) \ \ (2)\] dove il \(d\) giusto è ottenuto con una procedura per tentativi successivi. A questo punto sembrerebbe che il progetto di evitare le equazioni abbia tutti gli ingredienti per funzionare: possiamo fare le previsioni e volendo trovare le equazioni di evoluzione \({\bf x}_{j+1}= {\bf f}({\bf x}_j)\) ove la funzione \({\bf f}(\,)\) è ottenuta dagli analoghi con un’ opportuna procedura di ottimizzazione.

Un analogo esiste sicuramente, ce lo assicura il teorema di ricorrenza di Poincarè: un sistema deterministico, con uno spazio delle fasi limitato, dopo un certo tempo ritorna, quasi sempre, vicino alla sua condizione iniziale. Abbiamo un risultato rigoroso e la rivoluzione dei Big Data ci permette di ottenere e analizzare velocemente moli impressionanti di dati: sembra a questo punto che l’idea di soppiantare le equazioni con i dati abbia un fondamento. Ma è fattibile?

Non proprio. Ci sono infatti due ostacoli difficilissimi da aggirare, uno di natura metodologica e uno di natura pratica. Cominciamo da quest’ultimo: quanto indietro si deve andare per trovare l’analogo giusto, la cui esistenza è appunto garantita dal teorema di Poincaré? La risposta, già intuita da Boltzmann nel suo acceso dibattito con Zermelo sul problema dell’ irreversibilità, è un risultato ben noto della teoria dell’ergodicità (Lemma di Kac): il tempo medio di ritorno in una regione \(A\) è proporzionale all’ inverso della probabilità \(P(A)\) che il sistema si trovi in \(A\) \[\langle T_R \rangle= {\tau \over P(A)}\] ove \(\tau\) è un tempo caratteristico.
In un sistema di dimensione \(D\) (per la precisione se il sistema è dissipativo \(D\) è la dimensione frattale dell’ attrattore) la probabilità \(P(A)\) di stare in una regione \(A\) che in ogni direzione ha un’estensione percentuale \(\epsilon\) è proporzionale a \(\epsilon ^D\), quindi \(\langle T_R \rangle \sim \epsilon^{-D}\), se \(D\) è grande (diciamo oltre \(6- 7\)) già per precisioni non enormi (ad esempio \(5 \%\), cioè \(\epsilon= 0.05\)) il tempo di ritorno è talmente grande che in pratica non si osserva la ricorrenza, e equivalentemente non si trova un analogo. Nell’ applicazione pratica del metodo Takens si ha lo stesso problema: il valore di \(d\) dipende dal sistema (è proporzionale a \(D\)), quindi se la dimensione è grande, come conseguenza del Lemma di Kac, per poter usare la procedura si deve avere un \(M\) che cresce esponenzialmente con \(D\), quindi il metodo è di fatto non utlizzabile appena \(D\) supera il valore di \(6-7\).

L’altro ostacolo, come si diceva, è metodologico. I risultati di Takens permettono la ricostruzione dello spazio delle fasi di un sistema deterministico. Ma come osservato sopra, non esiste alcuna ragione per assumere che i problemi di interesse nelle scienze sociali possano essere governati da leggi deterministiche, così come per le scienze della vita. L’entusiasmo che porterebbe ad applicare il metodo EDM di Sugihara alla biologia e alla finanza non sembra dunque poggiare su alcun fondamento.
Nell’intervista riportata su Quanta Magazine, Sugihara si riferisce direttamente al metodo di Takens e alle nuove opportunità che questo offre alla luce dei Big Data: permette ai dati di dire quali sono le relazioni rilevanti. È interessante ricordare, a questo proposito, che alla fine degli anni 80, subito dopo cioè l’introduzione del risultato di Takens, l’entusiasmo fu grande. Così come il numero degli articoli fioriti su questa scia, ma errati in modo eclatante (anche su riviste come Nature e Science). La fonte di errore era la mancata comprensione dell’impossibilità di utilizzare il metodo per dimensioni alte. Intervenne addirittura David Ruelle per ribadire che, per sperare di poter utilizzare il metodo, la serie avrebbe dovuto essere abbastanza lunga diciamo \(M = 10^{2 D}\), senza contare i problemi pratici come la precisione dei dati, ma purtroppo la valanga di articoli senza senso non si arrestò.

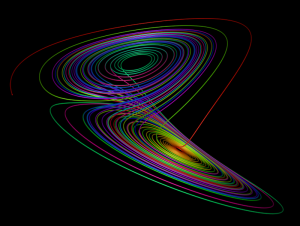
L’attrattore di Lorenz in 3D

Lorenz (uno dei padri moderni del caos) negli anni sessanta provò ad utilizzare il metodo degli analoghi per fare le previsioni meteo nel Nord America, e la sua conclusioni fu: “c’è da aspettarsi che il metodo sia destinato a fallire per l’alta probabità di non trovare alcun analogo accettabile nella storia passata dell’atmosfera”. L’impossibilità di trovare un analogo in una serie di qualche decina di anni è ovviamente dovuta al valore (enorme) di \(D\) nel problema considerato da Lorenz.
L’idea di base del modo in cui ora si fanno le previsioni meteo venne proposto negli anni 20 da Richardson (che aveva capito come l’ approccio in termini di analoghi non poteva che fallire), è il seguente: l’atmosfera evolve in accordo con le equazioni dell’idrodinamica e la termodinamica, quindi dallo stato presente dell’atmosfera, risolvendo (ovviamente numericamente) un sistema di equazioni alle derivate parziali, si può effettuare una previsione del tempo. La realizzazione del progetto visionario di Richardson è iniziata solo negli anni 50 con lo sviluppo di tre ingredienti assolutamente non banali: a) la messa a punto di equazioni efficaci; b) algoritmi numerici veloci; c) computer per i calcoli numerici.
Il punto a) è ovviamente l’ aspetto concettualmente più importante, nel caso della meteorologia fu necessario il contributo fondamentale di Charney e von Neumann che capirono come le equazioni originariamente proposte da Richardson, benchè corrette, non fossero adatte per le previsioni; il motivo è che sono troppo accurate, infatti descrivono anche moti ondosi ad alta frequenza che sono irrilevanti in ambito meteorologico. È quindi necessario costruire equazioni efficaci in cui non compaiano le variabili veloci.

È veramente sorprendente che, nonostante Poincaré abbia chiaramente stigmatizzato gli eccessi di un empirismo ingenuo: la scienza si costruisce con i fatti, come una casa con le pietre; ma una raccolta di fatti non è una scienza più di quanto un mucchio di sassi non sia una casa, i risultati rigorosi, i molti precedenti, i caveat di Ruelle, dopo tanti anni si insista ancora nel vecchio ingenuo sogno di una scienza puramente induttiva basata solo sulle osservazioni. Anzi, che slogan come “la fine della teoria”, “la fine delle equazioni” eccetera, continuino a far notizia e a influenzare, in modi più o meno diretti, le politiche della ricerca. Forse i motivi sono da ricercare nel fatto che anche la politica è stata sedotta dalle promesse di oggettività, automazione ed efficienza della rivoluzione Big Data?

Rimanendo in ambito strettamente scientifico, ecco un consiglio per una cura sicura: studiare i classici, i lavori dei grandi scienziati del passato (Boltzmann, Poincaré, Lorenz, Richardson, von Neumann) e magari qualche buon libro in cui le cose sopra discusse sono ampiamente trattate.

Hykel HOSNI, Dipartimento di Filosofia, Università di Milano
Angelo VULPIANI, Dipartimento di Fisica, Università Sapienza di Roma

Alcuni riferimenti

* C. Anderson The End of Theory: The Data Deluge Makes the Scientific Method Obsolete http://www.wired.com/2008/06/pb-theory/
* F. Cecconi, M. Cencini, M. Falcioni and A. Vulpiani The prediction of future from the past: an old problem from a modern perspective American Journal of Physics 80, 1001 (2012)
*  M. Cencini, F. Cecconi and A. Vulpiani Chaos: From Simple Models to Complex Systems (World Scientific, Singapore, 2009)
* A. Dahan Dalmedico History and Epistemology of Models: Meteorology as a Case Study Archive for History of Exact Sciences 55, 395 (2001)
* M. Giaquinta e H. Hosni La Matematica nelle scienze sociali: alcune considerazioni sulla teoria della scelta e del benessere sociale Lettera Matematica 93, 17 (2015)
* T. Hey , S. Tansley and K. Tolle (curatori) The Fourth Paradigm: Data Intensive Scientific Discovery (Microsoft Research, 2009).
* H. Hosni and A. Vulpiani Forecasting in the light of Big Data Philosophy and Technology (2017) https://doi.org/10.1007/s13347-017-0265-3
* M. Kac On the notion of recurrence in discrete stochastic processes Bull. Am. Math. Soc. 53, 1002 (1947)
* E.N. Lorenz Atmospheric predictability as revealed by naturally occurring analogues J. Atmos. Sci. 26, 636 (1969)
* P. Lynch The Emergence of Numerical Weather Prediction: Richardson’s Dream (Cambridge University Press, 2006)
* G. Popkin A Twisted Path to Equation-Free Prediction, Quanta Magazine, Ottobre 2015
* A. Vulpiani Lewis Fry Richardson: scienziato visionario e pacifista Lettera Matematica 90, 23 (2014)
* A.S. Weigend and N.A. Gershenfeld (Curatori) Time Series Prediction: Forecasting the Future and Understanding the Past (Addison-Wesley, 1994)
* H. Yea, R.J. Beamish, S.M. Glaser, S.C.H. Grant, C. Hsieh, L.J. Richards, J.T. Schnute and G.Sugihara, Equation- free mechanistic ecosystem forecasting using empirical dynamic modeling PNAS, E1569 (2015)

Roberto Natalini

Roberto Natalini [coordinatore del sito] Matematico applicato. Dirigo l’Istituto per le Applicazioni del Calcolo del Cnr e faccio comunicazione con MaddMaths!, Archimede e Comics&Science.