Alberto Gandolfi, professore presso la New York University Abu Dhabi, ha da poco pubblicato un articolo dal titolo “Planning of school teaching during Covid-19[1 ]A. Gandolfi (2020): Planning of school teaching during Covid-19, Physica D: Nonlinear Phenomena Volume 415, January 2021, 132753” (pianificare l’insegnamento scolastico durante il Covid-19). Di seguito commenta per noi alcuni risultati ottenuti in questa ricerca.
Uno dei aspetti più problematici della recente epidemia di Covid-19 e degli interventi volti a limitarne la diffusione riguarda le scuole: subito dopo aver accertato l’arrivo del contagio, praticamente tutti i paesi del mondo hanno chiuso le scuole e spostato le lezioni online. Questo ha comportato che nel mondo più di un miliardo di studenti [2 ]”COVID-19 Educational Disruption and Response”. UNESCO. http://www.iiep.unesco.org/en/covid-19-educational-disruption-and-response-13363. Retrieved 2020-05-24. abbia dovuto cambiare metodo di studio nel giro di poche settimane, con insegnanti e scuole che hanno dovuto adottare frettolosamente nuove tecniche didattiche per l’insegnamento a distanza: oltre ai notevoli disagi già arrecati a studenti, insegnanti e famiglie vi saranno anche effetti di lunga durata, ora difficilmente prevedibili[3 ]”Adverse consequences of school closures”. UNESCO. 2020-03-10. https://en.unesco.org/covid19/educationresponse/consequences. Retrieved 2020-03-15. [4 ]Gli effetti del Covid sulla scuola: Italia tra i paesi con la chiusura pi\uu lunga, ma con le classi tra le meno affollate, tgcom24, 22 settembre 2020.. In Italia le scuole hanno chiuso il 4 marzo fino a fine anno scolastico. Anche la riapertura autunnale è stata complicata in tutto il mondo [5 ]R. Ciano: Prepping to reopen, California schools desperate for guidance, money. CALmatters, Retrieved 2020-01-05.; le scuole italiane sono state praticamente tutte riaperte a settembre con severe misure di controllo, ma già tutte le scuole sono state chiuse in Campania oltre ad un centinaio di altri istituti nel paese, tra le proteste di tanti studenti. In questa situazione sarebbe auspicabile avere degli strumenti scientifici che permettano di ancorare il dibattito ad alcuni elementi possibilmente oggettivi, o almeno con una certa solidità matematica.
In uno studio recente [6 ]A. Gandolfi (2020): Planning of school teaching during Covid-19, Physica D: Nonlinear Phenomena Volume 415, January 2021, 132753 abbiamo adattato a questo scopo un modello compartimentale, tipo SIR, per modellizzare l’evoluzione dell’epidemia in una generica scuola, e definito un funzionale costo per evidenziare l’effetto delle eventuali scelte ed un possibile processo di ottimizzazione. Il modello ha permesso di mettere a fuoco le caratteristiche principali del contagio e le potenzialità di intervento; ma è anche emersa la necessità di tre dati statistici senza i quali è difficile fare previsioni affidabili; purtroppo, come discusso più avanti, in molti paesi tra cui l’Italia, non si effettuano campionamenti tali da permettere una stima accettabile di questi parametri.
Usando tuttavia i dati disponibili in Italia al momento, e facendo qualche ipotesi ragionevole circa il valore dei parametri, la conclusione che si trae dal modello è che non vi sono al momento le condizioni di sicurezza sufficienti per mantenere le scuole aperte in tutto il paese, nemmeno in modalità mista. Questo avrebbe potuto essere fatto a settembre, ma la recrudescenza del virus lo rende insostenibile ora. Per stabilire quanta parte della nuova ondata epidemica sia dovuta all’apertura della scuola, ossia se un’apertura più contenuta a settembre avrebbe ridotto l’impatto della nuova ondata, occorre un modello più ricco, che integri anche l’evoluzione del virus nella società, ma l’indicazione corrente è purtroppo che le scuole andranno tutte chiuse in tempi brevi.
Poiché le scuole sono comunque aperte in questo momento, si potrebbe sfruttare questa situazione per un breve periodo di rilevamento dati, al termine del quale passare ad una programmazione più consapevole.
Un modello matematico per la singola scuola
Utilizziamo un modello compartimentale basato su sistemi di equazioni differenziali [7 ]vedi per esempio:
C. Castellano, Il virus corre sulla rete, MaddMaths!, 12 maggio 2020., adattando la versione originale SIR alla descrizione di una singola scuola. I compartimenti considerati sono i suscettibili \(S(t)\) non ancora contagiati, gli esposti \(E(t)\) che sono stati contagiati e sono presintomatici ma contagiosi (una fase molto rilevante per studiare la diffusione del virus), gli infetti sintomatici \(I(t)\), gli asintomatici \(A(t)\), che sono contagiosi, e i guariti \(R(t)\). Si è inoltre aggiunto un termine \(\alpha\), definito in letteratura sorgente esterna, relativo alla possibilità di contagio all’esterno della scuola: si è visto poi, dallo studio del modello, la centralità di questo termine legato alla prevalenza di infetti nella regione in cui si trova la scuola. Riassumendo, le equazioni utilizzate per descrivere l’andamento dell’infezione in una scuola tipica sono: \[\begin{aligned}
\text{Suscettibili:}\quad\frac{dS}{dt} & =-\alpha (1-c(t)) S-\beta S c(t) (E+ \eta A)\nonumber\\
\text{Esposti:}\quad\frac{dE}{dt} & =\beta S c(t) (E+ \eta A)+
\alpha (1-c(t)) S-(\gamma+\delta)E \nonumber\\
\text{Asintomatici:}\quad\frac{dA}{dt} & = \gamma E
-\rho A \label{sistema}\\
\text{Infetti:}\quad\frac{dI}{dt} & = \delta E-\rho I\nonumber\\
\text{Guariti:}\quad\frac{dR}{dt} & =\rho (A+I)\nonumber\end{aligned}\] Data la scarsa probabilità di decessi, specialmente in una popolazione prevalentemente giovane come gli individui di una scuola, si è trascurata la mortalità. Il tempo è stato considerato in ore.
La principale novità del sistema riportato qui sopra rispetto ad un generico modello compartimentale è il coefficiente \(c(t)\), che assume valore \(0\) quando la scuola è chiusa, e vale \(1\) nelle sette ore dei giorni in cui la scuola viene tenuta aperta; \(c(t)\) modellizza quindi il controllo che ha l’autorità scolastica di optare per lezioni frontali (\(c=1\)) o a distanza (\(c=0\)). Una rapida applicazione di risultati standard permette di dimostrare che, nonostante il controllo non sia continuo, la soluzione del sistema è unica [8 ]Garrett Birkhoff, Gian-Carlo Rota – Ordinary differential equations-Wiley (1989).
La determinazione dei parametri
I modelli compartimentali sono molto sensibili a cambiamenti nel valore dei parametri, che quindi andrebbero determinati con cura. Purtroppo però vengono effettuati ben pochi rilevamenti finalizzati alla stime necessarie, da cui deriva una notevole difficoltà ad elaborare previsioni accurate.
Alcune simulazioni del modello precedente mostrano che tre parametri sono di primaria importanza; per ognuno, discutiamo il significato, alcune modalità ideali di stima, e la stima che ne diamo sulla base degli scarsi dati disponibili.
- Il coefficiente \(\alpha\) misura il rischio di contagio all’esterno della scuola (che abbiamo assunto attivo solo quando non c’è lezione – sia essa in presenza o online). Questo è legato alla diffusione del virus nell’area in cui si trova la scuola; più precisamente è un multiplo della prevalenza dei casi attivi non accertati, tramite un fattore, discusso in [9 ]A. Gandolfi (2020): Planning of school teaching during Covid-19, Physica D: Nonlinear Phenomena Volume 415, January 2021, 132753, che in Italia vale circa \(0.0176\). Purtroppo, non vi sono dati relativi alla prevalenza degli attivi non accertati, proprio perchè non accertati. Per stimare quantità di questo tipo esistono molti metodi, per esempio quello in [10 ]B\”ohning et al. (2020): Estimating the undetected infections in the Covid-19 outbreak by harnessing capture-recapture methods, International Journal of Infectious Diseases, 97, 197-201., basati su campionamenti casuali: con l’attuale prevalenza dei casi attivi di circa il 2-3 per mille, basterebbe fare per qualche giorno circa \(5\) mila test a caso, oltre ai circa \(150\) mila che si fanno giornalmente, per avere un quadro statisticamente affidabile di quanti casi non siano osservati. Vista l’assenza di rilevamenti e dati al riguardo, alcune considerazioni sulla base delle caratteristiche del virus e del numero giornaliero di tamponi suggeriscono che i casi attivi non rilevati siano circa pari a quelli rilevati (per avere un termine di paragone, il rapporto non rilevati su rilevati è stato stimato attorno a \(1,3\) in aprile in Austria [11 ]Prem K, Cook AR, Jit M (2017) Projecting social contact matrices in 152 countries using contact surveys and demographic data. PLoS Comput Biol 13(9): e1005697. https://doi.org/10.1371/journal.pcbi.1005697, e oggi siamo in una situazione simile come diffusione del virus, ma con più tamponi, quindi un fattore \(1\) non è privo di senso: varie stime più accurate indicano che il rapporto di \(1:1\) sia sensato al momento).
- Il coefficiente di trasmissibilità \(\beta\) all’interno della scuola si riferisce al numero di potenziali contatti infettivi a scuola, durante il trasporto e l’uscita. Questo numero è molto difficilmente stimabile, in particolare perchè si deve assumere una naturale tendenza a non seguire rigorosamente le misure di distanziamento che vengono imposte. Un dato di questo tipo potrebbe essere rilevato facendo un campionamento di scuole, ed utilizzando per i ragazzi più grandi i dati dei cellulari rilevati da un app tipo Immuni. Con test del genere si avrebbe un’idea dell’efficacia delle misure di distanziamento. In mancanza di tali dati, le valutazioni fatte qui si basano vari studi passati sui contatti in ambiente scolastico nei vari paesi , ridotti di un fattore dovuto a consapevolezza del rischio e misure di distanziamento.
- Il terzo coefficiente è la percentuale \((1-\eta)\) di pre- ed asintomatici che viene rilevata e quindi isolata dall’ambiente scolastico. Anche per questo come per \(\alpha\), basterebbe fare test a campione: qui si potrebbero selezionare una decina di scuole a caso e testare tutta la popolazione scolastica ed il personale per avere un dato affidabile. In assenza di tali rilevamenti, abbiamo considerato vari valori dal \(40\%\) circa che sembra corrispondere alla situazione della popolazione in generale, fino ad un ideale \(90\%\), che potrebbe essere il risultato dell’uso di test rapidi e frequenti.Poiché \(\beta\) ed \(\eta\) compaiono insieme, considereremo i valori del prodotto; indicativamente, con il livello di tamponi che vengono fatti attualmente e una moderata attenuazione dei contatti, il valore di riferimento è \(\beta \eta=50 \times 10^{-3}\).
Scuole aperte o chiuse?
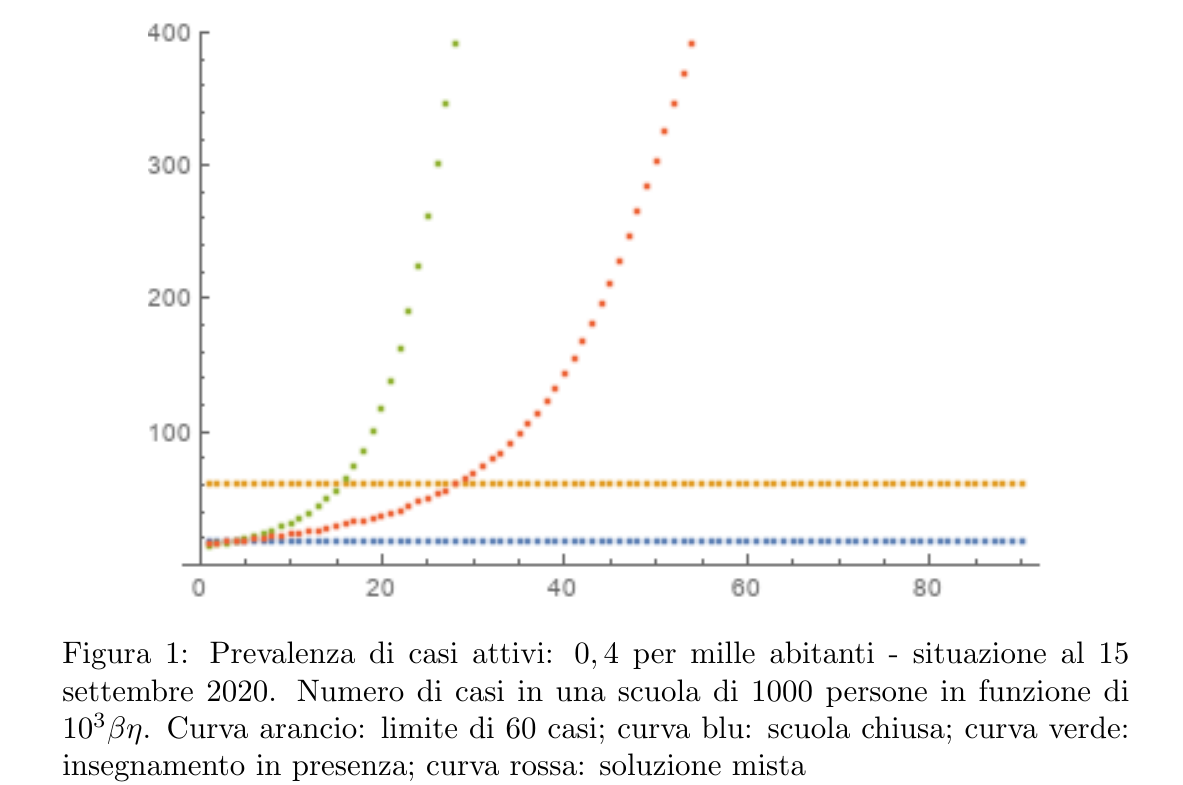
La prima parte dell’analisi è consistita nel confrontare le due opzioni di scuole aperte o con lezioni tutte a distanza. Abbiamo scelto indicativamente un limite di \(60\), tra sintomatici e asintomatici, nei primi due mesi di apertura di una scuola di \(1000\) persone. Il modello indica che con una prevalenza di casi attivi nell’area della scuola dello \(0,4\) per mille abitanti circa, che era la situazione al \(15\) settembre \(2020\) in gran parte dell’Italia, l’apertura della scuola era possibile solo in condizioni di grandissimo controllo: come riportato nel grafico in Figura 1, a scuola chiusa si potevano prevedere circa una ventina di casi nei primi due mesi (curva blu), mentre a scuola aperta (curva verde) il numero di casi sarebbe stato dell’ordine delle centinaia, a meno che \(\beta \eta < 15 \times 10^{-3}\). Quest’ultima condizione avrebbe richiesto test rapidi e frequenti a tutta la scuola, e misure strette di distanziamento.
In [12 ]A. Gandolfi (2020): Planning of school teaching during Covid-19, Physica D: Nonlinear Phenomena Volume 415, January 2021, 132753 si calcola che in una situazione standard la riapertura della scuola con moderate misure di controllo potesse essere fatta solo con una prevalenza dei casi attivi nel paese minore di \(50\) casi per milione di abitanti, una condizione in cui si trovavano a settembre solo pochi paesi tipo China, Tailandia e alcuni paesi africani.
Un funzionale di costo e l’ottimizzazione delle aperture
Per tentare di trovare una possibile soluzione al problema di assicurare almeno una parte di didattica frontale abbiamo poi provato a modellizzare gli obiettivi contrastanti di contenimento della diffusione del virus e riduzione del numero di giorni a distanza. Lo strumento adeguato è un funzionale \[\label{LLL}
\mathcal{L}=(S_0(T)-S_c(T)) +(N(c)/\tau)\] in cui \(T\) è l’orizzonte temporale, \(S_0(T)\) il numero di suscettibili alla fine del periodo nell’ipotesi che le scuole non vengano aperte mai, \(S_c(T)\) e \(N(c)\) il numero di suscettibili alla fine del periodo e il numero di giorni di lezioni a distanza nell’ipotesi che le scuole vengano aperte con la modalità prescritta dal controllo \(c\). L’elemento fondamentale di questo funzionale è però \(\tau\), che rappresenta il peso relativo di due obiettivi. In particolare, \(\tau/100\) rappresenta il numero di giorni di lezione frontale che viene ritenuto equivalente ad un incremento dell’\(1\%\) degli infetti; in varie simulazioni abbiamo assunto che si tratti di circa \(5\)–\(10\) giorni.
L’ottimizzazione ora si fa minimizzando rispetto ai possibili controlli \(c\). Se si considera l’intero anno scolastico, e una scelta di didattica in classe o a distanza per ogni settimana, il numero di possibillità è \(2^{40}\), e diventa \(2^{200}\) se la scelta è fatta per ogni giorno del calendario scolastico. Occorrono quindi dei sistemi di ottimizzazione discreta, quali il simulated annealing o gli algoritmi genetici, per trovare controlli \(c\) ottimali, o almeno vicini a quelli ottimali.
Soluzioni miste a settimane alterne
Le indicazioni sull’apertura delle scuole trovate ottimizzando il funzionale per ragionevoli valori di \(\tau\) sono risultate essere per lo più soluzioni con settimane alternate di didattica in presenza e a distanza. In figura 2 si vede l’andamento delle funzioni epidemiche nel caso di una soluzione ottimale, o quasi; si noti la differenza con il tipico modello SIR, in cui le funzioni sono molto più lisce ed il numero di suscettibili decresce molto più rapidamente.
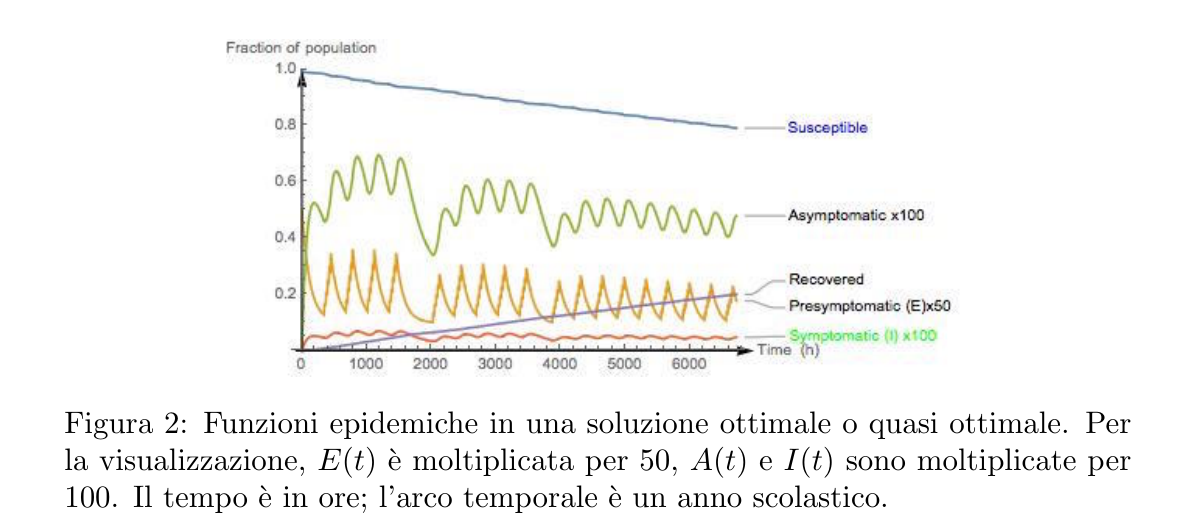
Soluzioni miste di questo tipo sono state in effetti ipotizzate in vari paesi, tra cui la Scozia [13 ]Coronavirus: What is a blended model of learning?
By Catherine Lyst BBC Scotland, Retrieved 2020-01-05. , e vengono proposte in questi giorni in vari contesti italiani. Queste soluzioni apparentemente permettono di sfruttare al meglio il periodo di incubazione e di positività del virus, di circa \(5\) e \(7\) giorni rispettivamente, in modo che la maggior parte dei contagi della settimana in presenza vengano risolti durante la settimana di didattica a distanza (più i due fine settimana). Per valori ragionevoli di \(\tau\) la riduzione della diffusione del virus è tale che rinunciando a circa la metà del tempo in presenza si può riuscire a contenere l’eccesso di casi nella scuola fino ad una prevalenza di circa \(500\) casi per milione. In aggiunta, si è visto che soluzioni con giorni alterni non permettono significativi miglioramenti rispetto all’alternanza settimanale. La curva rossa in figura 1 mostra il numero di casi a \(60\) giorni con la soluzione ottimale per \(\tau=800\); si vede che un moderato distanziamento e controllo su pre- ed asintomatici la condizione italiana di settembre sarebbe stata sostenibile con aperture miste. Molti paesi erano nella stessa situazione.
Una volta che soluzioni a settimane alterne sono state suggerite dal processo di ottimizzazione, e che se ne sono compresi i meccanismi di contenimento dell’infezione, rimane da valutarne il possibile impatto didattico, e la fattibilità.
Anche se a prima vista può non apparire, dal punto di vista didattico queste soluzioni offrono alcuni vantaggi:
- sono potenzialmente sostenibili, al contrario del clima di incertezza che si crea con un’apertura completa plausibilmente indirizzata a improvvise chiusure;
- permettono poi di sfruttare le potenzialità di entrambe le tecniche didattiche, magari riservando laboratori ed esami nelle settimane in presenza, e altre attività più individualizzate nelle settimane di didattica a distanza;
- permettono di monitorare più direttamente l’attività delle settimane a distanza durante le attività in presenza;
- offrono immediata flessibilità se la situazione locale dovesse improvvisamente cambiare in peggio, con un drastico aumento di casi, o in meglio, per esempio per la disponibilità di un vaccino: basterebbe continuare con una delle modalità senza eccessive difficoltà .
Per la loro implementazione, le soluzioni con settimane alternate richiedono notevoli sforzi sia da parte degli insegnanti e degli studenti, che devono riorganizzare le modalità pedagogiche e di apprendimento, sia da parte delle famiglie, che devono adattare i tempi a queste attività miste. Vi sono tuttavia alcuni elementi che renderebbero queste soluzioni meno complicate. Ad esempio, se un calendario a settimane alterne fosse adottato simultaneamente da tutte le scuole in una certa area, le attività commerciali circostanti potrebbe adattarsi parzialmente, concentrando il tempo libero dei genitori ed offrendo supporto nelle settimane di didattica a distanza.
Le complicazioni per implementare un metodo di insegnamento misto sono molteplici, ma sembrano offrire la possibilità di offrire una soluzione sostenibile con alcuni vantaggi pedagogici, in alternativa a soluzioni caratterizzate da bruschi cambiamenti o, peggio, dalla chiusura delle scuole per lunghi periodi.
La situazione attuale
Purtoppo la situazione al \(20\) ottobre \(2020\) è completamente compromessa. La prevalenza dei casi attivi di circa \(2.5\) per mille abitanti indica che l’insegnamento in presenza non è sostenibile, ma non lo è neppure una soluzione mista (figura 3), a meno di ridurre completamente i contatti tra studenti e tra il personale, sia a scuola che durante rientro e uscita (in modo da ridurre \(\eta\) di un fattore \(10\)) e di test generalizzati almeno settimanali (in modo da ridurre la possibilità di incotrare pre- ad asintomatici al \(10\%\)): un livello ottenibile praticamente con il solo lockdown. Nella situazione attuale anche a scuola completamente chiusa il numero di infetti tende, in assenza di altre misure, a superare il limite che avevamo indicato di \(60\) casi nei prossimi due mesi.
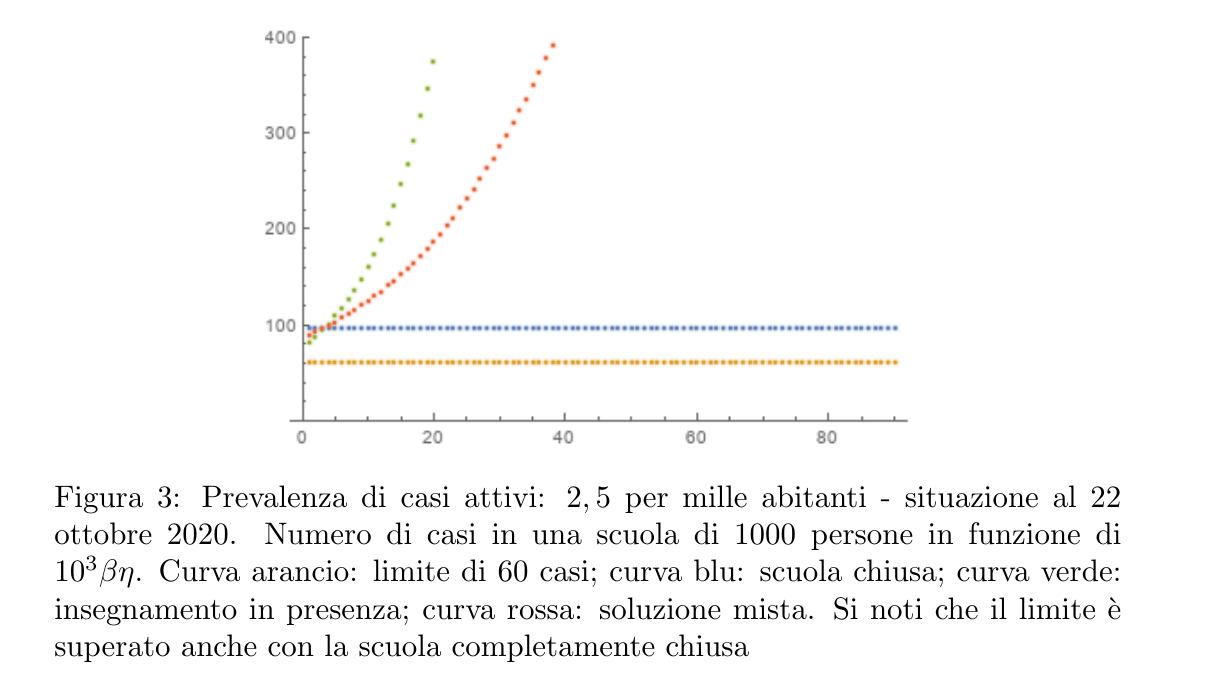
Visto che comunque le scuole sono aperte e che molteplici misure di contenimento delle trasmissioni sono state prese, si potrebbe usare questa situazione come un’occasione per una serie di rilevamenti che possano poi portare ad una programmazione consapevole e condivisa.
Si potrebbe usare una prima settimana per rilevare:
- la prevalenza del virus in macrozone: con 10.000 test per zona fatti su soggetti scelti a caso;
- la capacità dell’attuale sistema di screening di individuare pre- ed asintomatici nella scuola, effettuando test universali in qualche decina di scuole scelte a caso;
- l’efficacia del delle misure di distanziamento usando i dati dei cellulari in scuole scelte a campione.
La settimana successiva si potrebbe spostare le lezioni a distanza in tutte le scuole, utilizzando poi il necessario periodo di chiusura per valutare un modello misto sostenibile per la successiva riapertura.
Per capire quando questa sarà possibile, il modello presentato qui suggerisce di monitorare i casi attivi non rilevati. In mancanza di questo dato si può prendere, se il numero di tamponi si mantiene attorno agli attuali \(150\) mila giornalieri, il numero di casi attivi accertati. Attualmente ci sono circa \(155\) mila casi attivi; si potrà cominciare a riaprire le scuole in modalità miste e con mille precauzioni quando i casi attivi saranno meno di \(40\) mila, e con minime restrizioni quando i casi saranno meno di \(3000\), come successe per l’ultima volta il \(3\) marzo 2020 e succederà di nuovo dopo una vasta vaccinazione.
Alberto Gandolfi
New York University Abu Dhabi
Note e riferimenti
| ⇧1, ⇧6, ⇧9, ⇧12 | A. Gandolfi (2020): Planning of school teaching during Covid-19, Physica D: Nonlinear Phenomena Volume 415, January 2021, 132753 |
|---|---|
| ⇧2 | ”COVID-19 Educational Disruption and Response”. UNESCO. http://www.iiep.unesco.org/en/covid-19-educational-disruption-and-response-13363. Retrieved 2020-05-24. |
| ⇧3 | ”Adverse consequences of school closures”. UNESCO. 2020-03-10. https://en.unesco.org/covid19/educationresponse/consequences. Retrieved 2020-03-15. |
| ⇧4 | Gli effetti del Covid sulla scuola: Italia tra i paesi con la chiusura pi\uu lunga, ma con le classi tra le meno affollate, tgcom24, 22 settembre 2020. |
| ⇧5 | R. Ciano: Prepping to reopen, California schools desperate for guidance, money. CALmatters, Retrieved 2020-01-05. |
| ⇧7 | vedi per esempio: C. Castellano, Il virus corre sulla rete, MaddMaths!, 12 maggio 2020. |
| ⇧8 | Garrett Birkhoff, Gian-Carlo Rota – Ordinary differential equations-Wiley (1989) |
| ⇧10 | B\”ohning et al. (2020): Estimating the undetected infections in the Covid-19 outbreak by harnessing capture-recapture methods, International Journal of Infectious Diseases, 97, 197-201. |
| ⇧11 | Prem K, Cook AR, Jit M (2017) Projecting social contact matrices in 152 countries using contact surveys and demographic data. PLoS Comput Biol 13(9): e1005697. https://doi.org/10.1371/journal.pcbi.1005697 |
| ⇧13 | Coronavirus: What is a blended model of learning? By Catherine Lyst BBC Scotland, Retrieved 2020-01-05. |





















Trackback/Pingback