Pierre Berger è un ricercatore del CNRS francese. Lavora presso il Laboratoire d’Analyse, Géométrie et Applications dell’Université Paris 13. Di recente ha dimostrato alcuni teoremi che indicano che l’evoluzione di certi sistemi è scarsamente modellizzata dalle statistiche. François Béguin gli ha chiesto di spiegarci questi risultati. Articolo apparso il 5 maggio 2017 sul sito Images des Mathématiques e qui pubblicato con il permesso del sito e dell’autore. Traduzione a cura di Fabio Cristiani.

Buongiorno Pierre. Per prima cosa, ci puoi dire in che settore della matematica lavori ?
Mi occupo del comportamento dei sistemi dinamici caotici. Un sistema dinamico è semplicemente un sistema il cui stato si evolve nel tempo secondo una determinata legge chiamata legge di evoluzione. Tali sistemi ricorrono frequentemente in fisica, biologia, economia …
Viene proposto spesso come esempio il sistema solare. Lo stato del sistema in un dato istante è l’insieme delle posizioni e delle velocità dei diversi pianeti; la legge d’evoluzione è quella che dà l’accelerazione dei pianeti in funzione della loro posizione (grazie alla legge di gravitazione di Newton).
Un altro esempio classico è quello di un ecosistema composto da un piccolo numero di specie. Lo stato del sistema in un dato istante è il numero di individui di ciascuna specie. È possibile costruire modelli che forniscano una legge di evoluzione. Questa legge rifletterà considerazioni del genere “in un dato istante, la crescita del numero di pecore è proporzionale al numero di pecore, ma inversamente proporzionale al numero di lupi.”
Non è perché si è capaci di scrivere un sistema in equazioni — cioè determinare la sua legge di evoluzione —, che lo si capisce completamente. La legge di evoluzione ci dà lo stato del sistema nell’istante successivo. La sfida è quella di descrivere il suo comportamento per periodi di tempo molto più lunghi.
A volte il comportamento a lungo termine è molto semplice e molto regolare. Ad esempio, un pendolo (senza attrito) esegue un movimento di oscillazione periodica, perfettamente descrivibile a lungo termine (è questa regolarità che consente la fabbricazione di orologi!). Questo è anche il caso di due corpi isolati nello spazio sottoposti unicamente alla loro reciproca forza di attrazione (tipicamente una stella e un pianeta che le “gravità” intorno): la traiettoria di ciascuno di questi organi è una ellisse percorsa periodicamente.
La teoria del caos è nata quando Henri Poincaré ha scoperto che tre corpi isolati nello spazio (tipicamente una stella e due pianeti), soggetti solo alle loro reciproche attrazioni, possono avere traiettorie estremamente complesse. Poincaré ha scoperto che non siamo in grado di prevedere la posizione a lungo termine dei pianeti per due motivi. In primo luogo, non riusciamo a trovare una formula analitica che dia la posizione dei pianeti nel corso del tempo. Inoltre, se si simula l’evoluzione del sistema a partire da posizioni iniziali dei pianeti che siano leggermente diverse le une dalle altre, si possono scoprire traiettorie radicalmente differenti: un piccolissimo cambiamento nelle posizioni iniziali cambia completamente le traiettorie a lungo termine [1 ]H. Poincaré, Sur le problème des trois corps et les équation de la dynamique, Acta mathematica, 13, p. 1- 270 (1890) [2 ]Il risultato di Poincaré riguarda un sistema semplificato, e solo alcune posizioni e velocità iniziali molto particolari. Tuttavia, è stato recentemente mostrato che questo risultato teorico aveva manifestazioni nel nostro Sistema Solare. Utilizzando sofisticati algoritmi, Jacques Laskar e i suoi colleghi sono stati in grado di calcolare l’evoluzione del sistema solare su un periodo di diversi miliardi di anni. In questi calcoli, una variazione di meno di un centimetro nelle posizioni iniziali dei pianeti cambia completamente la faccia del sistema a lungo termine: queste minime variazioni delle posizioni iniziali possono comportare una collisione tra Mercurio e Venere, fra la Terra e Venere, o tra la Terra e Marte, in poco meno di quattro miliardi di anni! J. Laskar. Le Système Solaire est-il stable ? Séminaire Poincaré XIV (2010), page 242.
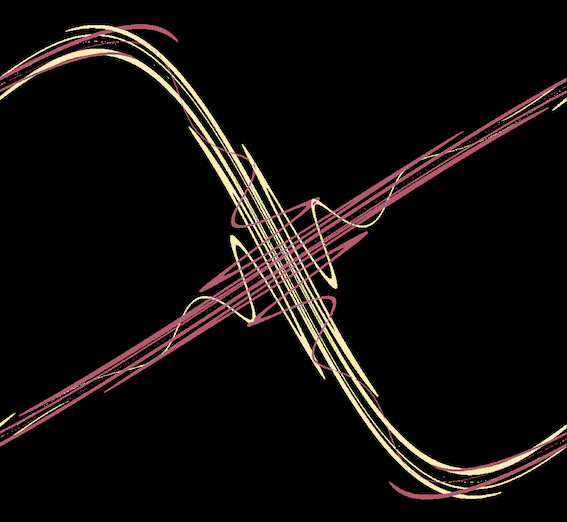
Immagine di un reticolo omoclino. Poincaré ha scoperto che questo figura geometrica impedisce di scrivere l’evoluzione di un problema a tre corpi sotto forma di una formula analitica: bisognerebbe prima di tutto saper descrivere attraverso funzioni analitiche la figura qui sopra, ciò che è impossibile perché le curve gialle e rosse si intersecano e si ripiegano in maniera troppo complessa.
Un sistema è detto caotico se un piccolissimo disturbo nel suo stato iniziale può sconvolgere completamente la sua evoluzione. La teoria del caos studia le proprietà dell’evoluzione di tali sistemi. Naturalmente, visto che si tratta di matematica, ci dimentichiamo il significato delle variabili che descrivono lo stato del sistema, considerando soltanto i valori. Questa astrazione permette di concentrarsi sui meccanismi matematici più semplici che generano un comportamento caotico.
I matematici che lavorano in questo settore cercano di classificare i sistemi dinamici a seconda della complessità del loro comportamento. A volte essi mostrano che alcune proprietà rimangono valide per una vasta classe di sistemi. Altre volte, al contrario, provano che molti sistemi non verificano talune proprietà attese… [3 ]Diversi articoli del sito IdM parlano di “caos”. Eccone uno elementare: Il mulino ad acqua di Lorenz
e altri due più avanzati: Sculture del caos e Hadamard e i sistemi dinamici
Tu hai recentemente dimostrato dei risultati che sostengono che alcune dinamiche possiedono un’infinità di “attrattori statistici”. Ci puoi spiegare di cosa si tratta?
Nelle scienze (umane, fisiche, biologiche, ecc), quando un sistema mostra un comportamento complesso lo si modella per difetto con probabilità e statistiche. Questo funziona molto bene per alcuni sistemi.
Si consideri ad esempio un sistema costituito da più palline in movimento in una scatola che collidano fra loro senza perdita di energia. Questo sistema ha un comportamento molto complesso: l’impatto tra le sfere fa cambiare loro direzione continuamente. Inoltre, come mostrato nell’immagine qui sotto, il minimo cambiamento nella posizione di una delle sfere modifica radicalmente le traiettorie di tutte le altre nel giro di un certo tempo: il sistema è caotico.
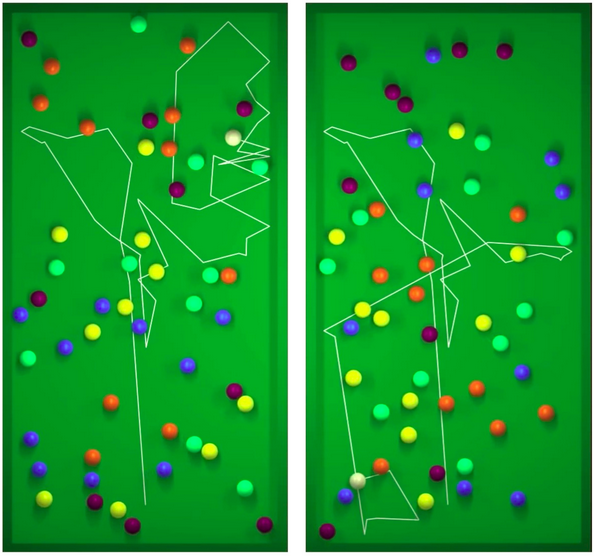
Simulazione numerica di un biliardo ideale privo di attrito, con cinquanta palle interagenti in seguito a collisioni perfettamente elastiche. La linea tratteggiata rappresenta la traiettoria della palla bianca. Le due immagini corrispondono all’evoluzione del sistema a partire da due stati iniziali leggermente diversi: una sola delle 50 palle è stata leggermente spostata. Ulteriori simulazioni sul sito del film Chaos (http://www-chaos-math.org/fr) da cui questa immagine è stata estratta.
Ma se guardiamo la posizione delle palle da un punto di vista statistico, allora otteniamo un risultato molto semplice. In media nel corso del tempo, ogni palla visiterà con la stessa frequenza ogni posizione e avrà la stessa frequenza di impatti con le pareti. Si tratta di una teorema di Yakov Sinai e Nandor Simanyi [4 ]N. Simányi, The K-property of N billiard balls I., Invent. Math. 108, p. 521–548 (1992).
Questo comportamento — caotico, ma nondimeno molto semplice da un punto di vista statistico — viene utilizzato nell’estrazione del lotto: i movimenti delle palline nelle macchine per l’estrazione sono molto complessi, non possiamo prevedere quale pallina uscirà, ma sappiamo che ogni pallina ha la stessa probabilità di uscita rispetto alle altre. Si può anche sperimentalmente verificare il teorema di Sinai e Simanyi mettendo un barometro in una stanza: la pressione misurata (vale a dire il numero di impatti delle molecole di aria sulla membrana del barometro per unità di tempo) non varia da un secondo all’altro e non dipende dalla posizione o dall’orientamento del barometro nella stanza.
Dire che un sistema ammette un numero finito di attrattori statistici significa sostanzialmente che il comportamento statistico di tale sistema è ben descritto da un numero finito di leggi di probabilità. Il comportamento di un tale sistema può essere caotico, ma lo si può capire se studiato da un punto di vista statistico.

Sheldon Newhouse
Fino a poco tempo fa, molti matematici erano ottimisti nel pensare che un sistema dinamico tipico non avesse che un numero finito di attrattori statistici. Si sapeva tuttavia dai risultati di Sheldon Newhouse [5 ]S.E. Newhouse, Diffeomorphisms with infinitely many sinks, Topology, 13, p. 9-18 (1974) che per alcuni sistemi dinamici, ci sono perturbazioni del sistema aventi un’infinità di attrattori con comportamenti statistici differenti. Tuttavia, si ipotizzava che queste perturbazioni fossero improbabili, non tipiche.
Tu parli di sistemi dinamici “tipici”. Di cosa si tratta? Perché interessarsi a sistemi tipici?
Da un lato, questo limita la possibilità di avere fenomeni patologici. Ad esempio, se prendiamo un sistema che non si evolve (la legge di evoluzione consiste nel “rimanere com’è”), allora ogni stato iniziale del sistema da luogo a un comportamento differente (che consiste nel rimanere in questo stato). Ci sono dunque tanti attrattori statistici quanto possibili stati iniziali. Tuttavia, il sistema ha un comportamento molto semplice e per niente caotico … Si vuole scartare questo tipo di comportamenti “degeneri” e concentrarsi verso comportamenti più “tipici”.
D’altra parte, se si parte con motivazioni fisiche, non dobbiamo dimenticare che qualsiasi modellazione passa per delle approssimazioni. Ad esempio, quando si mette in equazione il moto di un pendolo, generalmente si trascura il fatto che l’asta che sostiene il pendolo non è perfettamente rigida, che l’aria esercita attrito sul pendolo, etc. In altre parole, la legge di evoluzione del vero sistema fisico è una piccola perturbazione della legge di evoluzione del modello. Ecco perché, quando si studia il comportamento di un sistema dinamico, vorremmo idealmente trovare proprietà che siano “in prevalenza” soddisfatte da piccole perturbazioni di questo sistema.
Più in generale, non potendo avere proprietà valide per tutti i sistemi dinamici (o per tutti i sistemi di un certo tipo), si cercano proprietà valide per sistemi dinamici “tipici”, cioè per ” la maggior parte” dei sistemi dinamici.
Questo spiega il motivo per cui siamo interessati ai sistemi tipici. Ma come si fa a determinare se un sistema è “tipico” o no? In altre parole, come possiamo definire un sistema dinamico tipico?
È un po’ delicato. In primo luogo, parlare di sistemi dinamici tipici è una scorciatoia. Dovremmo parlare di “proprietà tipica” per i sistemi dinamici: una proprietà è chiamata “tipica” se vale per la maggior parte dei sistemi.

Andrey Kolmogorov
Resta da definire cosa si intende per “la maggior parte dei sistemi dinamici”. La prima idea che viene in mente è quello di prendere a caso dei sistemi dinamici, e dire che una proprietà è tipica se la probabilità di estrarre un sistema con questa proprietà è uguale a 1. Purtroppo, non possiamo formalizzare questa idea. Il problema è che per fare quest estrazione casuale, bisogna prima definire una misura di probabilità. Ad esempio, quando diciamo che estraiamo a caso un numero intero compreso tra 1 e 1000, si suppone che tutti i numeri abbiano la stessa probabilità di essere estratti, il che significa che consideriamo la misura di probabilità sul gruppo 1, …, 1000, che dà un peso di 1/1000 a ciascun elemento di questo gruppo. Ma si scopre che non c’è misura di probabilità “naturale” sull’insieme di tutti i sistemi dinamici. Questo è legato al fatto che l’insieme di tutti i sistemi dinamici è di dimensione infinita.
Ci sono stati varie proposte per aggirare questo problema. Una di esse è dovuta a A. Kolmogorov [6 ]Guardate l’articolo (in russo) di A. Kolmogorov nei Proceedings of the International Congress of Mathematicians 1954. Questo articolo è stato tradotto in inglese nel libro Foundations of Mechanics di R. Abraham et J. E.Marsden (Addison-Wesley Publishing Company) e consiste nel considerare perturbazioni di un sistema dinamico dipendenti da un parametro, e quindi tirare a sorte il valore del parametro. Questa volta è possibile perché il parametro è un numero, e c’è una probabilità molto naturale sull’insieme dei numeri.
Una proprietà è tipica se quando si tira a sorte il parametro, otteniamo un sistema che verifica questa proprietà con una probabilità pari a 1. È per questa nozione di tipicità “nel senso di Kolmogorov” che ho ottenuto risultati.
Che cosa avete dimostrato per questi sistemi “tipici”?
Fondamentalmente, ho mostrato l’esistenza di sistemi dinamici tipici nel senso di Kolmogorov che ammettono una infinità di attrattori statistici. Il comportamento di un tale sistema è modellato molto male dalle statistiche: piccole variazioni nello stato iniziale del sistema porteranno a evoluzioni completamente diverse, anche da un punto di vista statistico [7 ]P. Berger, Generic family with robustly infinitely many sinks, Inventiones Mathematicae, 205, 121 (2016)[8 ]P. Berger, Emergence and non-typicality of the finiteness of the attractors in many topologies, arXiv:1609.08803.
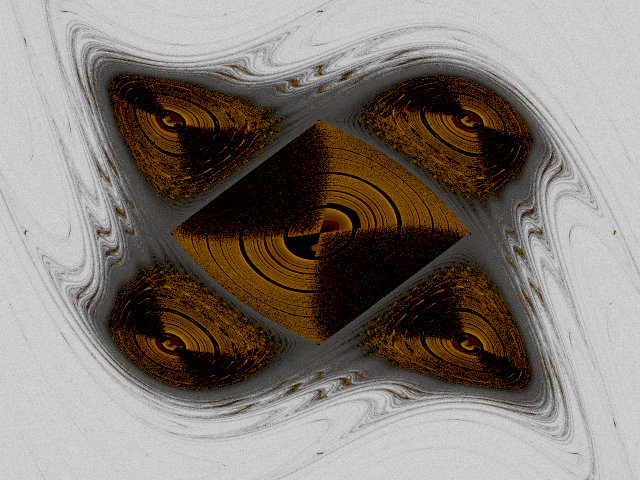
Un sistema dinamico (noto sotto il nome di standard map), che ha verosimilmente un numero infinito di attrattori statistici. L’immagine rappresenta l’insieme dei possibili stati del sistema. Ogni punto dell’immagine deve essere visto come un possibile stato iniziale del sistema. Le varie “macchie dorate” corrispondono a diversi insiemi di stati iniziali che potenzialmente daranno luogo a diversi comportamenti statistici del sistema.
In concreto, che significa il tuo risultato?
Questo risultato ci lascia di fronte a una scelta: o il concetto di tipicità come Kolmogorov non è pertinente per lo studio dei sistemi dinamici (in altre parole, i sistemi fisici reali non sono tipici nel senso di Kolmogorov), o – – e questo è il mio parere — ci sono in realtà molti sistemi fisici il cui comportamento è difficile, se non impossibile, descrivere statisticamente.
(Intervista a cura di François Béguin)
Note e riferimenti
| ⇧1 | H. Poincaré, Sur le problème des trois corps et les équation de la dynamique, Acta mathematica, 13, p. 1- 270 (1890) |
|---|---|
| ⇧2 | Il risultato di Poincaré riguarda un sistema semplificato, e solo alcune posizioni e velocità iniziali molto particolari. Tuttavia, è stato recentemente mostrato che questo risultato teorico aveva manifestazioni nel nostro Sistema Solare. Utilizzando sofisticati algoritmi, Jacques Laskar e i suoi colleghi sono stati in grado di calcolare l’evoluzione del sistema solare su un periodo di diversi miliardi di anni. In questi calcoli, una variazione di meno di un centimetro nelle posizioni iniziali dei pianeti cambia completamente la faccia del sistema a lungo termine: queste minime variazioni delle posizioni iniziali possono comportare una collisione tra Mercurio e Venere, fra la Terra e Venere, o tra la Terra e Marte, in poco meno di quattro miliardi di anni! J. Laskar. Le Système Solaire est-il stable ? Séminaire Poincaré XIV (2010), page 242 |
| ⇧3 | Diversi articoli del sito IdM parlano di “caos”. Eccone uno elementare: Il mulino ad acqua di Lorenz e altri due più avanzati: Sculture del caos e Hadamard e i sistemi dinamici |
| ⇧4 | N. Simányi, The K-property of N billiard balls I., Invent. Math. 108, p. 521–548 (1992) |
| ⇧5 | S.E. Newhouse, Diffeomorphisms with infinitely many sinks, Topology, 13, p. 9-18 (1974) |
| ⇧6 | Guardate l’articolo (in russo) di A. Kolmogorov nei Proceedings of the International Congress of Mathematicians 1954. Questo articolo è stato tradotto in inglese nel libro Foundations of Mechanics di R. Abraham et J. E.Marsden (Addison-Wesley Publishing Company) |
| ⇧7 | P. Berger, Generic family with robustly infinitely many sinks, Inventiones Mathematicae, 205, 121 (2016) |
| ⇧8 | P. Berger, Emergence and non-typicality of the finiteness of the attractors in many topologies, arXiv:1609.08803 |



















