Cosa c’entrano le collane e gli orecchini con i numeri primi? Alessandro Zaccagnini ce lo racconta, presentando al tempo stesso delle dimostrazioni senza formule (ma usando collane e orecchini, appunto) di due teoremi di teoria dei numeri: il Piccolo Teorema di Fermat e il Teorema di Wilson.
Dimostrazioni senza formule
In questo articolo vedremo due dimostrazioni combinatorie, senza formule, di due importanti risultati della Teoria Elementare dei Numeri. Il primo è il cosiddetto Piccolo Teorema di Fermat: se \(p\) è un numero primo ed \(a\) è un intero qualsiasi, allora \(p\) divide \(a^p – a\). Il secondo è il Teorema di Wilson, una semplice caratterizzazione dei numeri primi: l’intero \(n \ge 2\) è primo se e solo se \((n – 1)! – (n – 1)\) è divisibile per \(n\). Qui dimostreremo solo l’implicazione piú interessante: se \(p\) è un numero primo, allora \((p – 1)! – (p – 1)\) è divisibile per \(p\). In altre parole, esiste un numero intero \(k\) tale che \((p – 1)! = p – 1 + k p\).
In entrambi i casi costruiremo degli oggetti, collane e orecchini rispettivamente, fatti con perline colorate seguendo due diverse semplici regole. Suddivideremo questi oggetti in classi e conteremo il numero di oggetti in ciascuna classe: da questo conteggio seguiranno le tesi ricordate sopra.
Il Piccolo Teorema di Fermat
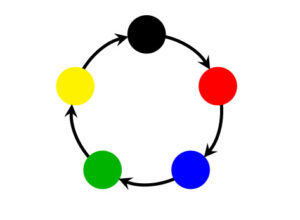
Consideriamo tutte le collane fatte con \(p = 7\) perline che possono avere uno dei sei colori rosso, blu, giallo, verde, nero, azzurro. In totale abbiamo \(6^7\) collane, delle quali \(6\) sono monocromatiche:
Ci interessano le restanti \(6^7 – 6 = 279\,930\) collane policrome, cioè con perline di almeno due colori diversi, che suddivideremo in classi di equivalenza. La classe di una collana policroma si ottiene facendola ruotare successivamente di un settimo di angolo giro. La figura illustra le collane di tre classi.
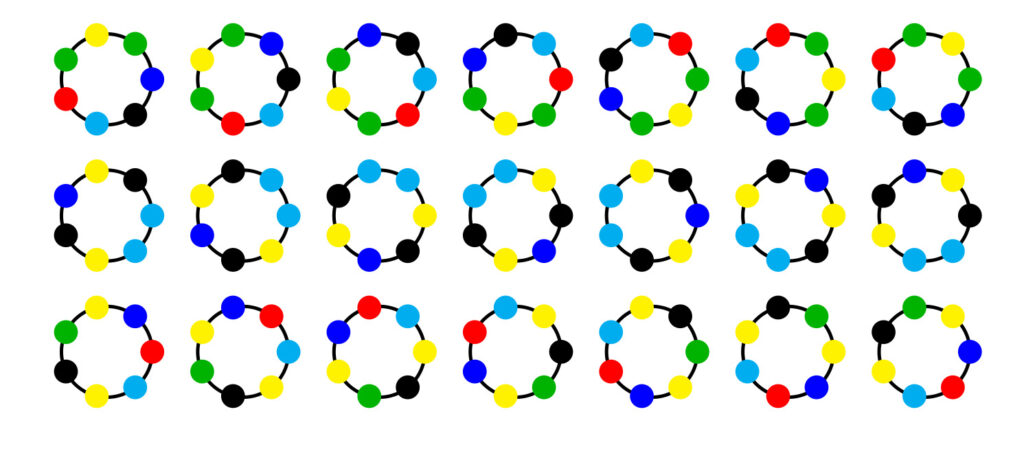
Ogni classe contiene esattamente \(7\) collane, e quindi \(7\) deve dividere \(6^7 – 6\). In generale, se abbiamo collane con \(p\) perline di \(a\) colori diversi, a parte le \(a\) collane monocromatiche, le altre \(a^p – a\) collane si possono suddividere in classi contenenti \(p\) collane ciascuna e quindi \(p\) divide \(a^p – a\).
Un lemma combinatorio
Dove precisamente stiamo usando l’ipotesi che \(p\) sia un numero primo? L’operazione di rotazione che usiamo per determinare la classe di una collana è periodica di periodo \(p\), o un suo divisore. Nelle due figure seguenti vediamo due collane con 8 perline ciascuna, in cui il periodo non è il massimo possibile:
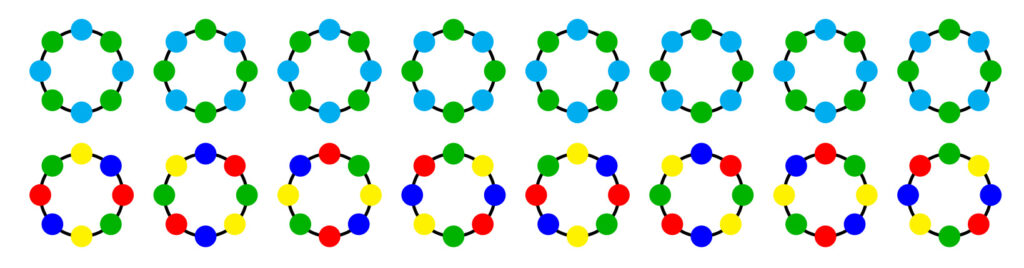
Se ruotando una collana policroma con \(n\) perline ritroviamo la collana di partenza prima di aver fatto \(n\) rotazioni, vuol dire che \(n\) ha un divisore non banale e quindi \(n\) non è un numero primo. In termini formali, la trasformazione di una collana in un’altra mediante rotazione di un \(n\)-esimo di angolo giro dà una successione periodica il cui periodo è un divisore di \(n\). Se \(n\) è un numero primo \(p\), il periodo può essere solamente 1 (per le collane monocromatiche) o \(p\) stesso (per tutte le altre collane).
Il Teorema di Wilson
Per la dimostrazione combinatoria del Teorema di Wilson costruiremo e conteremo alcuni orecchini colorati e troveremo per l’appunto che \((p – 1)!\) è \(p – 1\) piú un multiplo di \(p\). La dimostrazione che vedremo si applica la caso \(p = 5\): dimostreremo che \(4! = 24\) è uguale a \(4\) piú un multiplo di \(5\).
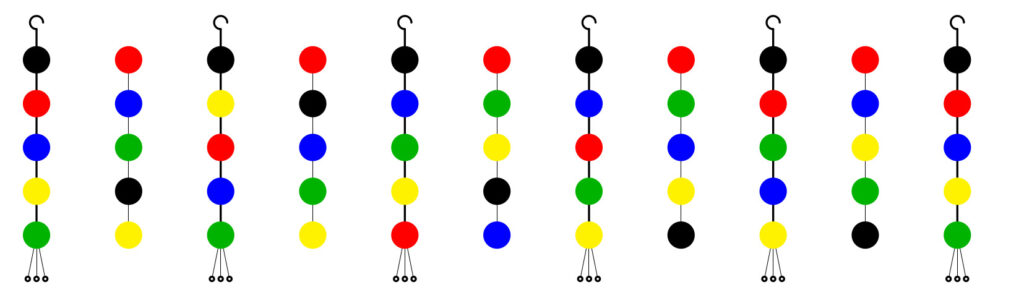
La prima cosa che vediamo è la sequenza dei 5 colori di cui abbiamo bisogno. Scegliamo questi cinque colori, e cioè il nero, il rosso, il blu, il verde e il giallo, che useremo in quest’ordine:
Le frecce indicano che ad ogni passaggio della costruzione ciascun colore si trasforma nel successivo in questo ordine. Il colore giallo si trasforma nel nero. Ora consideriamo tutti gli orecchini che si possono costruire secondo queste regole: in cima mettiamo un gancetto, poi mettiamo sempre una perlina nera, poi mettiamo le perline degli altri quattro colori in tutti i modi possibili, usando tutti colori distinti. In fondo, per indicare che l’orecchino termina, mettiamo un pendente. Gli orecchini saranno sempre fatti cosí: costruiremo degli oggetti intermedi che non saranno orecchini nel nostro senso perché non avranno la perlina nera al posto giusto, e noi li distingueremo dagli orecchini veri e propri perché non avranno le decorazioni, né il gancetto né il pendente.
In totale abbiamo \(4! = 24\) orecchini, che vediamo suddivisi nei sei in cui la seconda perlina è rossa, i sei in cui la seconda perlina è blu, poi verde o gialla. In definitiva, gli orecchini sono questi:
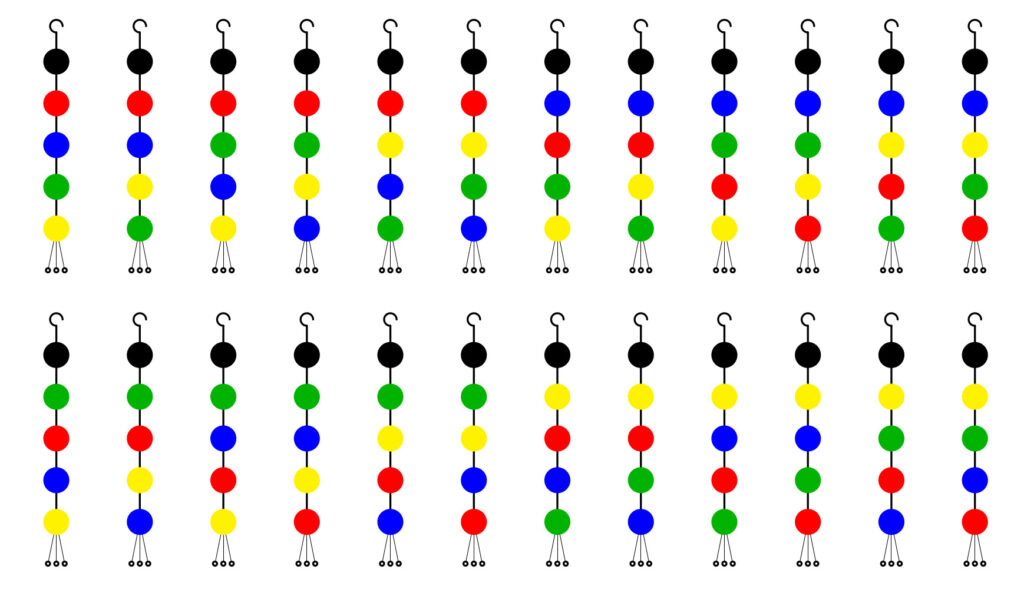
Vogliamo ora trasformare un orecchino in un altro e riunirli in classi, raggruppandoli, come abbiamo fatto per le collane nel paragrafo sul piccolo Teorema di Fermat. Dato un orecchino, cambiamo ciascuna perlina in quella del colore successivo della sequenza data sopra (NRBVGN). Poi tagliamo l’oggetto prodotto in due pezzi, che saldiamo riportando il nero in cima, mantenendo sempre la sequenza dei colori che abbiamo trovato. A questo punto mettiamo gancetto e pendente al nuovo orecchino. La figura illustra le due fasi della trasformazione. L’oggetto intermedio non è un orecchino perché non rispetta le regole che abbiamo detto (non ha il nero in cima), e quindi non ha le decorazioni. Invece, l’oggetto all’estrema destra soddisfa le regole e quindi è un orecchino a tutti gli effetti e gli mettiamo gancetto e pendente. Se seguiamo le regole date, cambiando ogni perlina in quella del colore successivo e poi tagliando la parte iniziale della figura intermedia per incollarla, cosí com’è, in fondo in modo che la perlina nera vada al primo posto, torniamo all’orecchino di partenza. Questa dunque non è una vera “trasformazione” perché questo orecchino torna ad essere sé stesso.
L’oggetto intermedio non è un orecchino perché non rispetta le regole che abbiamo detto (non ha il nero in cima), e quindi non ha le decorazioni. Invece, l’oggetto all’estrema destra soddisfa le regole e quindi è un orecchino a tutti gli effetti e gli mettiamo gancetto e pendente. Se seguiamo le regole date, cambiando ogni perlina in quella del colore successivo e poi tagliando la parte iniziale della figura intermedia per incollarla, cosí com’è, in fondo in modo che la perlina nera vada al primo posto, torniamo all’orecchino di partenza. Questa dunque non è una vera “trasformazione” perché questo orecchino torna ad essere sé stesso.
La stessa cosa succede prendendo quest’altro orecchino: Questa cosa però non succede sempre. Se noi prendiamo l’orecchino nella prossima figura e abbiamo la pazienza di eseguire tutti i passaggi che abbiamo detto, troviamo questa sequenza:
Questa cosa però non succede sempre. Se noi prendiamo l’orecchino nella prossima figura e abbiamo la pazienza di eseguire tutti i passaggi che abbiamo detto, troviamo questa sequenza:
Qui abbiamo indicato tutti i passaggi da fare, e gli oggetti intermedi che dobbiamo produrre, ma abbiamo omesso le frecce delle figure precedenti. Chiaramente dopo uno o 5 passaggi torniamo all’orecchino di partenza perché la sequenza si ripete con periodo 5 (e 5 è un numero primo, quindi non ha sottomultipli a parte 1 e 5 stesso). Suddividiamo ora gli orecchini in classi:
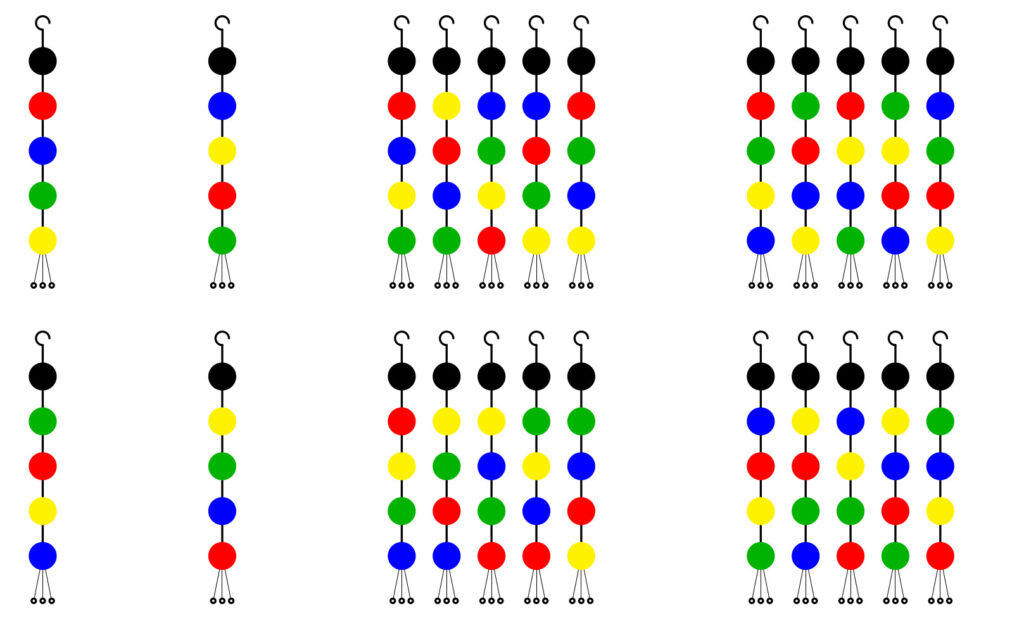
Abbiamo alcune classi che contengono 5 orecchini ciascuna, e quindi in totale un multiplo di 5. Poi abbiamo 4 orecchini in classi che ne contengono uno solo. Perché gli orecchini “solitari” sono esattamente questi 4?

La risposta a queste domande dipende dalla sequenza dei colori scelta all’inizio. Nel primo orecchino semplicemente seguiamo la sequenza naturale dei colori. Nel secondo prendiamo un colore ogni due (e quindi NBGRVN), nel terzo uno ogni tre (NVRGBN), nel quarto uno ogni quattro, o, che è la stessa cosa, percorriamo la sequenza al contrario.
Se saltiamo sempre lo stesso numero di colori, la trasformazione che abbiamo utilizzato in effetti non trasforma l’orecchino perché il risultato è sempre l’orecchino di partenza. Siccome possiamo passare dal nero ad uno qualsiasi degli altri 4 colori, dopo di che la sequenza è fissata una volta per tutte, avremo esattamente 4 orecchini in una classe per conto loro, mentre tutti gli altri sono collocati in classi, ciascuna delle quali contiene 5 elementi, come abbiamo visto sopra. Quindi abbiamo dimostrato ciò che volevamo.
In generale avremo bisogno di \(p\) colori; nei nostri orecchini il colore “nero” occuperà sempre la prima posizione, e quindi avremo \((p – 1)!\) orecchini in totale; di questi alcuni sono in classi che contengono esattamente \(p\) elementi, mentre gli altri \(p – 1\) sono “solitari.” Gli orecchini solitari corrispondono alle progressioni aritmetiche di ragione 1, 2, 3, …, \(p – 1\) ridotte modulo \(p\), e cioè alle sequenze \((0, 1, 2, 3, \dots)\), \((0, 2, 4, 6, \dots)\), \((0, 3, 6, 9, \dots)\), …. Il fatto che \(p\) sia un numero primo si usa nel momento in cui diciamo che ogni classe ha \(1\) o \(p\) elementi perché la trasformazione usata ha un periodo che divide \(p\).
Dietro le quinte
Per chi è curioso, questa è la versione della dimostrazione prima di passare ai colori: \[\begin{aligned}
(0,1,2,3,4) &\to (1,2,3,4,0) = (0,1,2,3,4) \\
(0,2,4,1,3) &\to (1,3,0,2,4) = (0,2,4,1,3) \\
(0,3,1,4,2) &\to (1,4,2,0,3) = (0,3,1,4,2) \\
(0,4,3,2,1) &\to (1,0,4,3,2) = (0,4,3,2,1) \\
(0,1,2,4,3)
&\to (1,2,3,0,4) = (0,4,1,2,3) \to (1,0,2,3,4) = (0,2,3,4,1) \\
&\to (1,3,4,0,2) = (0,2,1,3,4) \to (1,3,2,4,0) = (0,1,3,2,4) \\
&\to (1,2,4,3,0) = (0,1,2,4,3) \\
(0,1,3,4,2)
&\to (1,2,4,0,3) = (0,3,1,2,4) \to (1,4,2,3,0) = (0,1,4,2,3) \\
&\to (1,2,0,3,4) = (0,3,4,1,2) \to (1,4,0,2,3) = (0,2,3,1,4) \\
&\to (1,3,4,2,0) = (0,1,3,4,2) \\
(0,1,4,3,2)
&\to (1,2,0,4,3) = (0,4,3,1,2) \to (1,0,4,2,3) = (0,4,2,3,1) \\
&\to (1,0,3,4,2) = (0,3,4,2,1) \to (1,4,0,3,2) = (0,3,2,1,4) \\
&\to (1,4,3,2,0) = (0,1,4,3,2) \\
(0,2,1,4,3)
&\to (1,3,2,0,4) = (0,4,1,3,2) \to (1,0,2,4,3) = (0,2,4,3,1) \\
&\to (1,3,0,4,2) = (0,4,2,1,3) \to (1,0,3,2,4) = (0,3,2,4,1) \\
&\to (1,4,3,0,2) = (0,2,1,4,3)\end{aligned}\]
I numeri 0, 1, 2, 3, 4 corrispondono rispettivamente ai colori nero, rosso, blu, verde, giallo. I primi 4 orecchini corrispondono alle progressioni aritmetiche di ragione 1, 2, 3 o 4 ridotte modulo 5, e sono i “punti fissi” della trasformazione, cioè gli orecchini solitari. Gli oggetti preceduti dal simbolo \(\to\) sono i prodotti intermedi della trasformazione e non sono orecchini nel nostro senso perché non cominiciano con 0. La classe trattata in dettaglio sopra corrisponde alla sequenza che comincia con \((0, 1, 2, 4, 3)\) cioè all’orecchino con i colori nero, rosso, blu, giallo, verde.
Riferimenti
L’idea di questo articolo è suggerita da Anderson, Benjamin & Rouse[1 ]P. G. Anderson, A. T. Benjamin, and J. A. Rouse, Combinatorial proofs of Fermat’s, Lucas’s, and Wilson’s theorems, Amer. Math. Monthly 112 (2005), 266–268.. Il principale strumento usato è un lemma combinatorio nel quale si contano i “punti fissi” di particolari classi di permutazioni di oggetti, le perline colorate nella nostra metafora; nel caso del Piccolo Teorema di Fermat i punti fissi sono le collane monocromatiche, in quello del Teorema di Wilson sono gli orecchini solitari.
Nel mio video sul Piccolo Teorema di Fermat[2 ]A. Zaccagnini, Il piccolo Teorema di Fermat, 2021, Video-pillola su YouTube. https://youtu.be/Zd0BG9ccAN8 si possono trovare varie dimostrazioni, tra cui quella data qui. Nel mio primo video sul Teorema di Wilson[3 ]A. Zaccagnini, Come riconoscere i numeri primi? Il teorema di Wilson, 2020, Video-pillola su YouTube. https://youtu.be/mubwg24FJzE c’è la dimostrazione aritmetica di entrambe le implicazioni; nel secondo c’è la dimostrazione riportata qui[4 ]A. Zaccagnini, La dimostrazione combinatoria del Teorema di Wilson, 2022, Video-pillola su YouTube. https://youtu.be/ctJcNeeEHpY.
Note e riferimenti
| ⇧1 | P. G. Anderson, A. T. Benjamin, and J. A. Rouse, Combinatorial proofs of Fermat’s, Lucas’s, and Wilson’s theorems, Amer. Math. Monthly 112 (2005), 266–268. |
|---|---|
| ⇧2 | A. Zaccagnini, Il piccolo Teorema di Fermat, 2021, Video-pillola su YouTube. https://youtu.be/Zd0BG9ccAN8 |
| ⇧3 | A. Zaccagnini, Come riconoscere i numeri primi? Il teorema di Wilson, 2020, Video-pillola su YouTube. https://youtu.be/mubwg24FJzE |
| ⇧4 | A. Zaccagnini, La dimostrazione combinatoria del Teorema di Wilson, 2022, Video-pillola su YouTube. https://youtu.be/ctJcNeeEHpY |