Una chiacchierata sulla topologia: 3 – Giocare con lo spazio

da Gabriele Belegni | 28 Settembre 2024 | Una chiacchierata sulla topologia | 0 commenti

Una mini-serie a cura di Gabriele Belegni, dove esploreremo i concetti principali di una delle branche più affascinanti della matematica: la topologia. Cercheremo di scoprire le motivazioni e le idee che hanno spinto ad introdurre certi concetti concentrandoci sull’aspetto intuitivo piuttosto che su quello formale. Oggi scopriremo come giocare con gli spazi topologici, deformandoli come se fossero fatti di pongo. Trovate tutte le puntate su questa pagina.

Nelle scorse puntate abbiamo conosciuto la materia prima della topologia: gli spazi topologici. Ora dobbiamo solo capire come lavorarli, come deformarli senza strapparli o incollarli. Queste deformazioni hanno un nome: omeomorfismi.

Prendiamo due spazi topologici, chiamiamoli $X$ e $Y$ ad esempio, e proviamo a vedere come si costruisce un omeomorfismo pezzo dopo pezzo. Per prima cosa ci servirà una funzione di $X$ in $Y$ , chiamiamola $f$ (se non siete familiari con le funzioni, pensate a $f$ come ad un macchinario che prende elementi di $X$ e li trasforma in elementi di $Y$ ). Per evitare che $f$ strappi dei “pezzi” di $X$ possiamo richiedere che $f$ sia continua. Molti di voi si ricorderanno che, informalmente, una funzione continua è una funzione il cui grafico, dove essa è definita, può essere tracciato senza staccare la penna dal foglio… ma questo che c’entra con gli strappi? Vedetela così: questa idea di continuità vale per funzioni di $\mathbb{R}$ (cioè la retta) in $\mathbb{R}$ , ed il grafico di $f$ altri non è che la retta ma deformata. Se posso disegnare questo grafico senza staccare la penna dal foglio vuol dire che nella deformazione non vengono compiuti strappi (figura 1). Come si fa spesso in matematica, si prende un’idea semplice e la si cerca di adattare a contesti più generali; nel nostro caso bisogna adattare (e formalizzare) la nozione di continuità a funzioni definite tra spazi topologici come $f$ . Sorvoliamo per ora questo passaggio, gli interessati possono trovarlo nella sezione in fondo alla pagina, altrimenti potete tranquillamente proseguire immaginando una funzione continua come una trasformazione che non compie strappi.

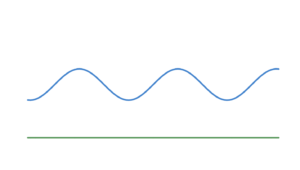
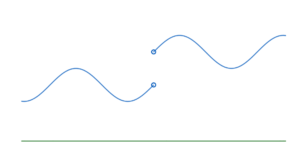
Figura 1: A sinistra una funzione continua, si noti che la retta verde viene deformata nella curva blu senza strappi. A destra, una funzione non continua, dove in effetti la retta verde viene strappata.

Bene, abbiamo risolto il problema degli strappi, ma ancora non siamo sicuri che non vengano incollati dei pezzi. Potrebbe accadere che punti diversi di $X$ vengano trasformati da $f$ in uno stesso punto (figura 2) e che quindi ci sia un incollamento. Per proibire ciò basta richiedere che $f$ sia iniettiva, il che vuol dire che $f$ trasforma punti distinti di $X$ in punti distinti di $Y$ .

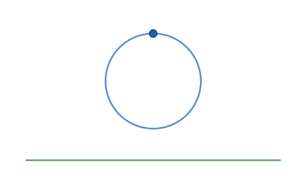
Figura 2: Con una funzione non iniettiva potremmo incollare i due estremi del segmento verde (ottenendo ad esempio la circonferenza blu).

Una funzione continua e iniettiva è quindi priva di strappi e cuciture. Perfetto, abbiamo trovato gli omeomorfismi! Non esattamente, purtroppo. Una funzione continua e iniettiva permette di deformare $X$ senza strappi o cuciture, ma quello che otteniamo non è, in generale, tutto $Y$ , ma solo una sua parte. Potrebbe quindi esserci una porzione di $Y$ “strana”, o comunque non legata a $X$ , il che sarebbe abbastanza fastidioso, e per evitare ciò richiediamo che la funzione sia anche suriettiva, cioè che ogni punto di $Y$ provenga da un qualche punto di $X$ o, più semplicemente, che $f$ trasformi $X$ in tutto $Y$ senza lasciar fuori nulla. Ok, ora ci siamo! Quasi, datemi ancora un attimo.

Ora la nostra funzione è iniettiva e suriettiva, e quindi invertibile, cioè esiste una funzione (che indichiamo con $f^{-1}$ ) che fa esattamente il contrario di ciò che fa $f$ , riporta tutto $Y$ in $X$ invertendo il procedimento seguito da $f$ . La funzione inversa è a sua volta iniettiva e suriettiva, ma in generale nulla ci dice che è anche continua, potrebbe quindi capitare che per tornare da $Y$ a $X$ si debba strappare qualcosa. Che ci importa, $X$ si deforma in $Y$ senza strappi o cuciture, era quello che volevamo no? Vero, vero, ma in matematica siamo un po’ puntigliosi su queste cose. Nella prima puntata (ma come, non l’hai letta?! Tieni, ecco il link) dicevamo che il cuore della geometria è studiare oggetti equivalenti sotto certe trasformazioni, che nel caso della topologia sono gli omeomorfismi. Se posso passare da $X$ a $Y$ senza strappare né cucire, ma non riesco a fare la stessa cosa passando da $Y$ a $X$ , allora questi due spazi non sono proprio equivalenti, non per un topologo. E va bene, ma se richiedessi che anche $f^{-1}$ sia continua sarei a posto no? Sì, perfetto, così posso tornare da $Y$ in $X$ senza strappare nulla!

Ecco che siamo finalmente arrivati alla definizione:

Un omeomorfismo tra due spazi topologici $X$ e $Y$ è una funzione $f$ di $X$ in $Y$ continua, invertibile e con inversa continua.

Se esiste un omeomorfismo tra $X$ e $Y$ vuol dire che possiamo deformare questi spazi uno nell’altro come desideravamo e diciamo che sono spazi omeomorfi. Un cerchio ed un quadrato sono omeomorfi, così come un segmento (aperto) e una retta, gli spazi verdi e blu in figura 1 a sinistra o, come nel celebre esempio, una tazza e una ciambella.

In topologia spazi omeomorfi sono sostanzialmente lo stesso oggetto, e fare topologia significa cercare di distinguere spazi, di capire se sono omeomorfi o no. Per affermare che due spazi sono omeomorfi basta trovare un omeomorfismo tra i due, ma dire che gli spazi non sono omeomorfi è molto più difficile, bisognerebbe infatti dimostrare che nessuna funzione tra i due soddisfa tutte le proprietà che la renderebbero omeomorfismo, cosa improponibile. A venirci in aiuto saranno le cosiddette proprietà topologiche, che renderanno il nostro lavoro immensamente più semplice e ci daranno molte informazioni sugli spazi in questione. Ne parleremo tra 2 puntate: nella prossima ci rilasseremo un po’ e vedremo alcuni esempi di spazi topologici e di omeomorfismi. A presto!

3 – continua

Per chi fosse incuriosito, diamo un’occhiata alla definizione formale di funzione continua. Clicca per continuare.

Dati due spazi topologici $X$ e $Y$ , diciamo che una funzione $f:X \to Y$ è continua se per ogni aperto $A$ di $Y$ , $f^{-1}(A)$ è un aperto di $X$ .

La prima cosa che salta all’occhio è l’uso di $f^{-1}$ : chi ci assicura che esista? Nessuno ci ha detto che $f$ è invertibile! C’è una sottigliezza: qui $f^{-1}$ non è l’inversa a cui siamo abituati, ma la cosiddetta inversa insiemistica. Dato un sottoinsieme $A$ di $Y$ , $f^{-1}(A)$ è il sottoinsieme di $X$ fatto da tutti e soli i punti di $X$ che, una volta applicata $f$ , vanno a finire in $A$ . Anche accettato questo non sembra chiaro perché si debba richiedere che l’inversa insiemistica (anche detta preimmagine) di un aperto sia ancora un aperto. In topologia vogliamo studiare gli omeomorfismi, che sono prima di tutto funzioni continue; dobbiamo quindi assicurarci che queste funzioni non alterino più di tanto la struttura di uno spazio topologico (altrimenti anche gli omeomorfismi lo farebbero). Ora, la struttura di uno spazio topologico è data essenzialmente dagli aperti; vogliamo quindi che una funzione continua si “comporti bene” con gli aperti, che non li modifichi troppo, in un senso che diventerà via via più chiaro. È la stessa cosa che si fa ad esempio in algebra lineare, dove si studiano spazi vettoriali e si cerca di determinare se essi sono o non sono isomorfi. Un isomorfismo è prima di tutto un’applicazione lineare, e in effetti un’applicazione lineare è definita come un’applicazione che rispetta la struttura di spazio vettoriale, cioè ne rispetta le operazioni. Richiedere che per ogni aperto $A$ di $Y$ $f^{-1}(A)$ sia un aperto ci assicura che tutto ciò che va a finire in un qualunque aperto di $Y$ proviene da un aperto, in questo senso una funzione continua rispetta la struttura di spazio topologico. Se avessimo richiesto quello che forse sembra più naturale, cioè che per ogni aperto $A’$ di $X$ , $f(A’)$ sia un aperto di $Y$ , non avremmo avuto un controllo altrettanto forte. In generale in $f(A’)$ , che è un sottoinsieme di $Y$ , si trovano sì tutti i punti che provengono da quelli di $A’$ , ma potrebbero esserci anche punti che provengono da un altro sottoinsieme di $X$ , $B’$ ad esempio, che non necessariamente è un aperto. Nonostante a primo impatto sembri abbastanza artificiale, questa definizione di continuità è la più potente e generale possibile, capace di racchiudere in sé anche la definizione a cui siamo stati abituati in analisi. Quest’ultima vale infatti per funzioni definite su spazi metrici, che ricordate sono dei particolari spazi topologici dove siamo in grado di misurare precisamente le distanze. Dunque, rileggendo la definizione dell’analisi si nota l’uso più o meno esplicito di una funzione distanza (che nel caso di funzioni reali è data dal modulo). 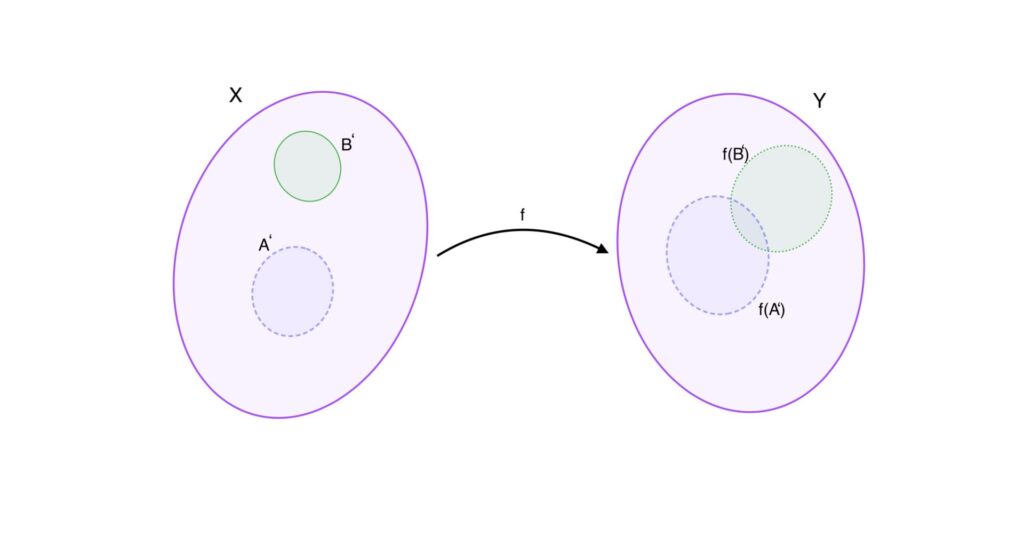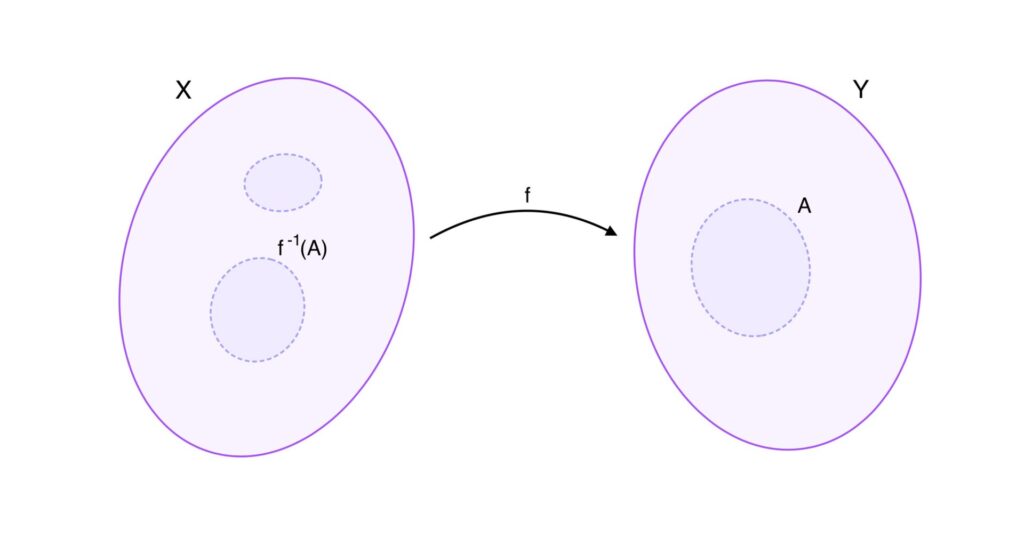Sopra si vede che in $f(A’)$ possono esserci anche cose che provengono da un altro sottoinsieme $B’$ . Sotto, $f^{-1}$ vista come inversa insiemistica.

Gabriele Belegni

Gabriele Belegni, laureato in Matematica teorica e studente magistrale in Matematica applicata presso l’Università di Camerino. Mi occupo anche della divulgazione matematica nelle sue varie forme: articoli, conferenze e laboratori.