Abbiamo parlato del sito Problemi per matematici in erba nell’articolo di Sofia Sabatti. Oggi vi riproponiamo dal sito un problema in video e la sua soluzione. Buona visione!
Per condividere con gli alunni il video che presenta questo problema, fornire il seguente link:
https://youtu.be/M8CSM9RHndo
Soluzione
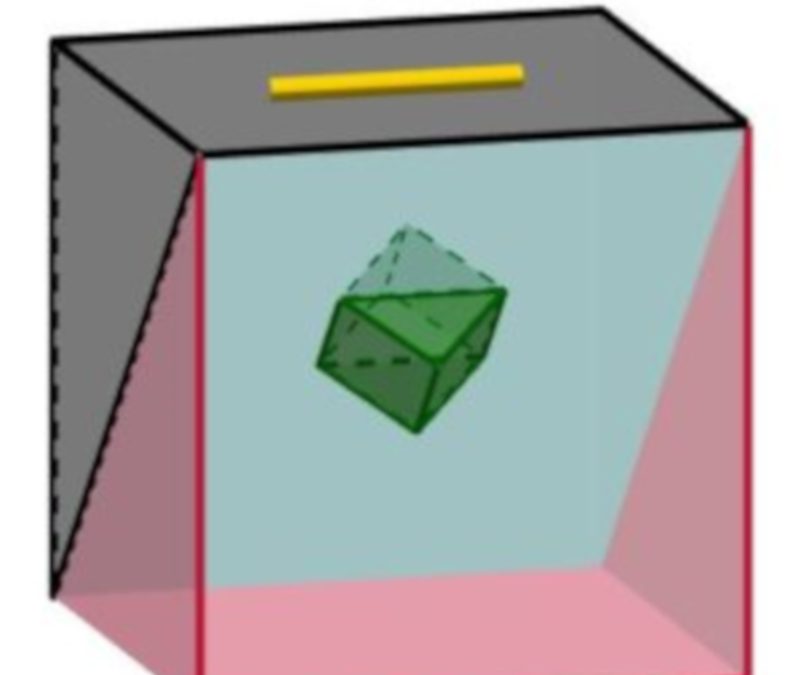
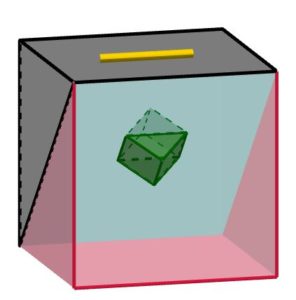
La forma del salvadanaio mostrato nel video è quella di un cubo: ha 6 facce, 12 spigoli e 8 vertici.
Rappresentiamo il salvadanaio con questo disegno, colorato in modo diverso rispetto all’oggetto reale, per poterne più facilmente descrivere le parti.
La faccia di questo cubo più vicina all’osservatore corrisponde alla finestrella trasparente del salvadanaio magico. Tutte le altre facce corrispondono alle facce opache del salvadanaio, che nella realtà sono completamente nere. La faccia superiore del salvadanaio è dotata di una fessura (rappresentata in giallo nel disegno): le monetine che vengono infilate in questa fessura sembrano scomparire.
Il “trucco” sta in questo: il rettangolo qui disegnato in azzurro è, nella realtà, uno specchio rivolto verso l’osservatore, che divide il salvadanaio in due settori non comunicanti. Le monetine infilate nella fessura rimangono nella parte “posteriore” del cubo (quella che nel disegno è colorata di grigio scuro). L’osservatore non nota subito la presenza dello specchio, perché esso è posto su un piano che è piano di simmetria per il cubo. Questo significa che la parte “anteriore” del cubo (quella che nel disegno è colorata in rosso) e la sua immagine riflessa formano per gli occhi dell’osservatore un cubo intero, proprio uguale a quello che si vedrebbe dalla finestrella se non ci fosse lo specchio all’interno.
Il cubetto che si vede sospeso nel vuoto (o nell’aria) all’interno del salvadanaio, rappresentato nella figura in verde, è formato da un oggetto reale e dalla sua immagine riflessa nello specchio. L’oggetto reale (rappresentato in verde scuro) è un prisma a base triangolare, le cui basi sono due triangoli rettangoli isosceli e la cui altezza è congruente ai cateti della base. Questo prisma è fissato allo specchio attraverso la vite che viene mostrata nella seconda parte del video. L’immagine riflessa di questo prisma è rappresentata nel disegno in verde chiaro: insieme al prisma verde reale, questa immagine forma proprio un cubo.
Nel video si chiede di descrivere che forma hanno le due parti in cui lo specchio divide il salvadanaio e di determinarne il volume, considerato che gli spigoli del salvadanaio misurano 7 cm.
Le due parti in cui lo specchio divide il salvadanaio sono due prismi, uguali tra loro, aventi per base un triangolo rettangolo isoscele (metà faccia del cubo) e per altezza lo spigolo del cubo.
Il volume di ciascuna di queste parti è quindi la metà di quello del cubo, ossia (7·7·7):2cm3 = 343:2cm3 = 171,5 cm3.
Si chiede poi di descrivere la forma dello specchio e di calcolare le sue dimensioni: si tratta di un rettangolo di dimensioni 7 cm (la lunghezza dello spigolo del cubo) e 7·√2 cm (la lunghezza della diagonale della faccia del cubo).
Messo da parte il salvadanaio magico “commerciale”, l’insegnante nel video si propone di costruirne uno artigianale usando come contenitore una scatola da scarpe di dimensioni 9cmx17cmx24cm e uno specchio. Nel video si nota che lo specchio a disposizione dell’insegnante “sta perfettamente” nella scatola da scarpe: il lato più lungo dello specchio è lungo come lo spigolo maggiore della scatola; il lato più corto dello specchio è lungo come la diagonale della faccia della scatola di dimensioni 9cmx17cm.
Per calcolare la misura del lato più corto dello specchio basterà quindi applicare il teorema di Pitagora, ottenendo: √(92+172) cm = √(81+189) cm = √270 cm.
La domanda cruciale rispetto al salvadanaio “fai da te” che l’insegnante si propone di costruire è questa: si otterrà ancora un salvadanaio magico?
In altre parole: costruendo un salvadanaio con quella scatola e quello specchio, posizionati come nel video, si potrà ritagliare una fessura da cui far entrare le monetine, in modo tale che esse scompaiano alla vista dell’osservatore e che questi non si accorga della presenza di qualcosa che divide la scatola in due settori non comunicanti?
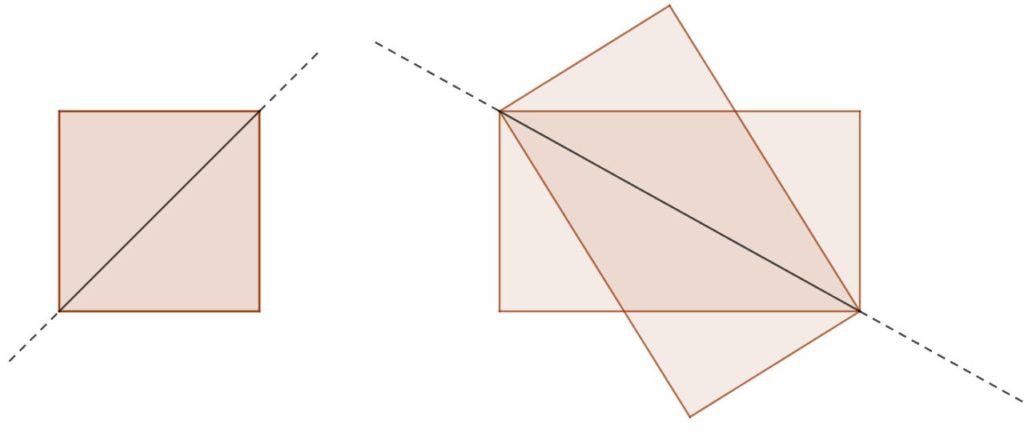
“La risposta a questa domanda è “No!”. In questo caso la parte anteriore del parallelepipedo e la sua immagine riflessa non formano agli occhi di chi osserva un parallelepipedo intero, perché il piano-specchio non è un piano di simmetria del parallelepipedo-scatola. Questo fa sì che l’immagine riprodotta dallo specchio non inganni affatto: non essendo questa immagine uguale alla parte nascosta di scatola, si capisce immediatamente la presenza di “qualcosa che non va”: una superficie riflettente che crea un settore nascosto all’interno della scatola.
Clicca per saperne di più
Commenti
Nel video con il quale presentiamo questo problema, sembriamo dare quasi per scontato che i ragazzi capiscano immediatamente qual è il “trucco” che fa scomparire le monetine infilate nel salvadanaio. Ebbene: per i bambini della scuola primaria questa scoperta non è affatto banale e di solito non lo è nemmeno per ragazzi più grandi (a meno che non abbiano già avuto tra le mani un oggetto simile). Se porteremo in classe un salvadanaio magico, sarà bene lasciare che gli alunni se lo passino, lo tengano in mano, lo guardino con attenzione, magari chiedendo a chi conosce già il trucco (o a chi lo scopre alla svelta) di tenerselo per sé per… qualche istante (di solito, di più non riescono!). Se invece racconteremo ai ragazzi questo problema proprio attraverso un video, sarà opportuno insistere con loro perché lo fermino nel momento in cui si chiede “Qual è il trucco?”, eventualmente “riavvolgendolo” e riguardandone la prima parte, finché non riescono almeno a formulare una ipotesi rispetto a ciò che causa l’apparente sparizione delle monete.
Un problema significativo
La simmetria
Il nodo cruciale attorno al quale questo problema è costruito è certamente la simmetria nel piano e nello spazio.
Già l’esercizio di immaginazione richiesto per dire quanti sono gli spigoli, i vertici e le facce del cubo (pur non avendolo tra le mani) è reso più semplice da alcune considerazioni sulla simmetria della figura. Ad esempio: se devo contare i vertici e ne vedo solo 6, fra cui tutti e 4 i vertici “di sopra”, posso comunque dire che in tutto sono 8; infatti, per ragioni di simmetria, so che per ciascuno dei 4 vertici che vedo “di sopra” ce n’è uno pure “di sotto”. Considerazioni analoghe possono essere fatte anche per stabilire quante sono le facce e quanti sono gli spigoli anche senza contarli a uno a uno.
La simmetria entra in gioco in maniera fortissima, poi, quando si tratta di scoprire il “trucco” del salvadanaio magico e di capire se funzionerebbe anche in quello “fai da te”.
- Nel salvadanaio a forma di cubo, il trucco funziona perché il piano su cui si fa giacere lo specchio è uno dei piani di simmetria della figura; in particolare, è un piano che passa per due spigoli opposti del cubo. Potrebbe essere interessante far contare ai ragazzi quanti piani di simmetria passanti per spigoli opposti ci siano in un cubo qualsiasi, per poi far loro notare anche, però, che nel caso del salvadanaio magico (in cui la faccia trasparente e quella con la fessura svolgono un ruolo particolare) di questi sei piani se ne può sfruttare – per realizzare il trucco – solo uno.
- Il trucco non funzionerebbe con la scatola di scarpe mostrata nel video, perché il piano per due spigoli opposti di un parallelepipedo che non ha facce quadrate non è un piano di simmetria del parallelepipedo.
Spesso, i bambini e i ragazzi interpellati in proposito ritengono invece che non faccia differenza usare un cubo o un parallelepipedo le cui facce non siano quadrate. Ci sembra di poter dire che ciò dipenda da una mis-concezione fortemente radicata anche in molti studenti della scuola secondaria di primo grado (se non oltre), ossia l’idea che la diagonale di un rettangolo sia un suo asse di simmetria. Tutta la seconda parte del problema (quella in cui si ipotizza di costruire un salvadanaio “fai da te” usando una scatola da scarpe) è stata inserita apposta per far “scontrare” i ragazzi con questi fatti:
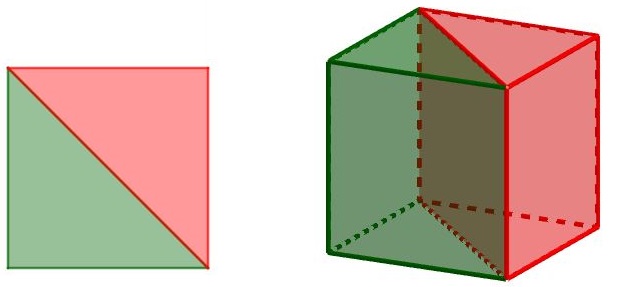
- la retta che contiene una diagonale è asse di simmetria del quadrato;
- la retta che contiene una diagonale NON è asse di simmetria di un rettangolo che non sia un quadrato.
Prismi e piramidi
Alcune richieste contenute nel video-problema, che a prima vista appaiono secondarie, possono contribuire a demolire altre mis-concezioni spesso radicate nei ragazzini. Ad esempio, la risposta immediata che abbiamo ricevuto più volte quando abbiamo chiesto che forma avessero le due parti in cui il cubo viene diviso dallo specchio è stata: “Sono due piramidi!”. Questa risposta, pur essendo sbagliata, non è da cassare e basta: si può cercare di capire insieme ai ragazzi da dove venga e quale buona idea contenga. Probabilmente la risposta nasce da una forse inconsapevole analogia tra un quadrato e un cubo e tra un triangolo e la piramide: come il quadrato è diviso dalla diagonale (asse di simmetria passante per due vertici opposti) in due triangoli, così – immaginano i ragazzi – il cubo sarà diviso dal piano di simmetria che passa per due spigoli opposti in due piramidi.
In realtà (e i ragazzini, riflettendoci un attimo, possono capirlo senza difficoltà), partendo da una quadrato diviso in due triangoli e “tirando su tutto per dritto” (come faremmo per ottenere il cubo), ciascun triangolo finisce con l’originare un prisma, non una piramide! Ecco allora che questo problema può diventare anche una buona occasione per discutere con gli alunni su che cosa sia una piramide, che cosa sia un prisma e come si possano definire in modo corretto.
lato e diagonale del quadrato
Un’altra domanda che trae in inganno i ragazzini è quella che chiede che forma abbia lo specchio nel salvadanaio magico. Spesso la prima risposta attorno alla quale si crea un certo consenso è che si tratta di un quadrato. E qualcuno rimane di questo parere anche quando gli si fa notare che uno dei lati dello specchio è lungo come lo spigolo del cubo e l’altro come la diagonale di una faccia del cubo, quasi che non fosse per loro evidente che il lato e la diagonale di un quadrato non possono avere la stessa lunghezza. Così, a partire da un problema “magico”, si può tornare a parlare di disuguaglianza triangolare, di ipotenusa e cateti di un triangolo rettangolo, di rapporto tra la diagonale e il lato di un quadrato.
Un problema memorabile grazie all’effetto sorpresa
Inutile cercare di sostenere il contrario: gli spettacoli di magia affascinano grandi e piccini, come si suol dire. E le monete che scompaiono alla nostra vista, appena vengono infilate in un salvadanaio, sono difficili da dimenticare!
Di questo dato di fatto possiamo approfittare nella speranza che ai nostri alunni rimanga in mente qualcosa a proposito di cubo, delle sue sezioni, dei suoi piani di simmetria. Ma, sempre a proposito di magia, c’è un ulteriore passo che potremmo compiere insieme a loro, di cui parleremo nel prossimo paragrafo.
Metacognizione
Nell’immaginario comune, la magia è quanto di più distante dalla matematica o dalla scienza possa esistere. Addirittura si pensa alla magia come a qualcosa che sfida le leggi della matematica e della fisica (o della chimica), dimostrandosi ad esse superiore.
Sarebbe una bella conquista se, con il contributo di problemi come questo, i nostri alunni imparassero non solo che conoscere un po’ di matematica e di scienze può aiutare a svelare i trucchi, ma anche che chi questi trucchi li inventa, non lo fa grazie a qualche capacità soprannaturale, bensì proprio grazie alle proprie conoscenze in campo matematico e scientifico.
Un problema aperto
Il salvadanaio mostrato nel video sembra “magico”, oltre che per la sua capacità di far scomparire le monete, anche perché ha un cubetto che sembra essere sospeso in aria nel bel mezzo del cubo. Nel video viene persino mostrata la vite che tiene fissata allo specchio una figura che dà origine a questa illusione ottica. Una buona domanda per proseguire nelle riflessioni potrebbe essere questa: quale forma ha l’oggetto fissato allo specchio con la vite?
In rete si trovano svariate immagini di salvadanai “a lievitazione” costruiti come questo; se ne potrebbero fornire alcune ai ragazzi per poi chiedere che forma devono avere gli oggetti fissati agli specchi nei vari casi.
Uno sviluppo interessante potrebbe essere quello di far costruire ai ragazzi un loro salvadanaio magico. In questo caso, però, si tratterebbe di un lavoro decisamente complesso, che mette in gioco competenze progettuali e gestionali di alto livello. Dal punto di vista strettamente legato alla matematica, porsi l’obiettivo di costruire davvero il salvadanaio richiederebbe di riflettere, innanzitutto, sullo spessore dei vari elementi reali (lo spessore dello specchio, lo spessore delle pareti del cubo), che non è trascurabile quando si progetta che misure devono avere i pezzi da procurarsi per la realizzazione. Inoltre sarebbe un buon modo per introdurre (o ritornare su) questioni legate alla misura e alla approssimazione.
Scenari possibili
“Il salvadanaio magico” si presta ad essere affrontato con ragazzi di età e di livello scolare differente, fermo restando il fatto che le domande andranno ogni volta adattate.
Lo stupore davanti alle monetine che scompaiono è assicurato a chiunque non conosca già il trucco, grande o piccolo che sia. I bambini della scuola primaria potranno ben comprendere l’effetto dello specchio, soprattutto se verrà data loro la possibilità, oltre che di rigirarsi il salvadanaio tra le mani, anche di aprirlo e di controllare la veridicità di ciò che nel video viene mostrato. I ragazzini della scuola secondaria di primo grado potranno, oltre che capire il trucco, descriverlo con il linguaggio specifico della matematica che ormai padroneggiano; potranno inoltre rispondere a tutte le domande poste nel video a proposito delle misure delle varie componenti del salvadanaio “originale” e di quello “fai da te”. Ragazzi più grandi, pensiamo in particolar modo a quelli che frequentano il primo biennio di un istituto tecnico o professionale, potranno progettare e realizzare un proprio salvadanaio magico “personalizzato”, magari anche variando la forma dell’oggetto che “lievita” sospeso all’interno.
Materiale necessario
Per risolvere questo problema così come viene proposto, non serve nulla di particolare. Diversa è la situazione nel caso in cui si voglia costruire davvero il salvadanaio: occorrerà fare un progetto accurato ed avere dei ritagli di balsa (per le 5 facce opache del cubo), un quadrato di plexiglas (per la finestrella) e uno specchio rettangolare di dimensioni opportune. Su una delle facce opache occorrerà intagliare una fessura, abbastanza grande da lasciar entrare le monetine. I vari pezzi potranno essere assemblati con della colla a caldo, ma… se si vuole poter recuperare le monetine, bisognerà avere l’accortezza di fare in modo che il coperchio con la fessura sia apribile…!