Alessandro Zaccagnini ci racconta di un progetto che ha realizzato con le docenti Maria Chiara Gullo e Lorenza Serventi dell’Istituto Comprensivo “Guatelli” di Collecchio (Parma), nel quale hanno fatto costruire agli allievi di due classi terze della Secondaria di primo grado due “grafi,” uno bidimensionale e l’altro tridimensionale, associati alla moltiplicazione dei numeri naturali; dopo la costruzione hanno usato gli oggetti per ottenere informazioni teoriche sulle proprietà dell’operazione. Vediamo cosa ne è venuto fuori.
Questo articolo è dedicato ad un laboratorio che ho coordinato nell’Istituto Comprensivo “Ettore Guatelli” di Collecchio, in provincia di Parma. A questo progetto hanno partecipato le stesse docenti e le stesse classi che sono state protagoniste del laboratorio sui “Gioielli della matematica” descritto qui [1 ]A. Zaccagnini. “I Gioielli Della Matematica.” Sito Web MaddMaths! https://maddmaths.simai.eu/didattica/i-gioielli-della-matematica/. (2024). Questa volta abbiamo realizzato alcune strutture che sono associate alla moltiplicazione fra numeri naturali: una descrizione piú dettagliata delle motivazioni si trova nell’articolo che ho scritto con Caterina Cozzani e Roberta Sandri[2 ]C. Cozzani, R. Sandri e A. Zaccagnini. “Collane, Orecchini E Scatolette — Costruzione Di Oggetti Matematici Con Materiali Della Vita Quotidiana.” Archimede 1: 2–19 (2024).; in particolare, facciamo riferimento al paragrafo 2 e alla Figura 2. Il mio interesse per i grafi associati alla moltiplicazione dei numeri naturali è all’origine anche dell’articolo [3 ]A. Zaccagnini. “Operazioni: Elementari, Ma Non Troppo!” Sito Web MaddMaths! https://maddmaths.simai.eu/divulgazione/focus/operazioni-elementari/ (2020)..
I grafi sono strutture astratte molto usate nelle applicazioni della matematica all’informatica perché possono rappresentare in modo efficace molte situazioni diverse ma con caratteristiche comuni. Si può pensare ad una carta stradale, alla rete ferroviaria, alla rete Internet o altre applicazioni come la rappresentazione delle varie fasi dell’esecuzione di un algoritmo, …
Nel nostro caso, siamo interessati a visualizzare l’effetto della moltiplicazione sui numeri naturali e per questo motivo abbiamo concretamente realizzato i grafi che ci aiutano in questo compito. In pratica abbiamo costruito due grafi basati sulle proprietà della moltiplicazione: si vedano le Figure qui sotto e le fotografie a corredo di questo articolo. Consideriamo il primo caso, quello del grafo bidimensionale, o meglio planare. Partendo dal numero 1, moltiplichiamo per 2 (frecce rosse) o per 3 (frecce blu) raggiungendo altri numeri naturali. Da ciascuno dei numeri raggiunti partono due nuove frecce con la stessa convenzione sui colori, e cosí via. In questo modo non possiamo raggiungere tutti i numeri naturali: per esempio non troviamo multipli di 5 o di 7. In modo analogo costruiamo il grafo tridimensionale: questa volta da ogni vertice del grafo partono tre frecce colorate, due come prima e una verde che rappresenta la moltiplicazione per 5; anche in questo caso notiamo che alcuni numeri naturali non compaiono.
Dopo la costruzione, avvenuta materialmente in un’aula dell’Ateneo di Parma, abbiamo spiegato alle due classi il significato degli oggetti realizzati, e in particolare le informazioni aritmetiche contenute. Una parte del materiale è stato preparato in anticipo, perché l’incontro in Università è durato complessivamente 3 ore circa: i dettagli sono descritti qui sotto.
Descrizione e preparazione del materiale
I materiali utilizzati per realizzare i due grafi descritti qui sotto sono tutti facilmente reperibili in commercio con una spesa molto modesta:
- 100 palline di polistirolo del diametro di 2cm;
- un pennarello nero;
- 100 stuzzicadenti;
- 3 colori a tempera (rosso, blu e verde nei nostri esempi);
- colla a caldo o vinavil;
- due quadrati di cartone robusto sufficientemente grandi;
- un paio di forbici robuste per tagliare il cartone.
Consigliamo di verificare in anticipo che la colla sia “compatibile” con il polistirolo e non lo sciolga.
Per realizzare i modelli proposti è necessario avere stuzzicadenti di due colori diversi (rosso e blu) per il caso bidimensionale, e di tre colori (rosso, blu e verde) per quello tridimensionale. Questi stuzzicadenti sono stati colorati con i colori a tempera prima dell’incontro all’Università, per permettere una perfetta asciugatura. Un certo numero di stuzzicadenti non colorati è necessario per dare stabilità alla struttura tridimensionale, ma si possono usare anche per la struttura bidimensionale; nelle nostre figure non sono mai stati indicati, ma sono ben visibili nelle fotografie.
Suggeriamo di numerare le palline di polistirolo prima dell’inizio dell’attività di laboratorio, dopo aver calcolato tutti i valori che compariranno, una volta decise le dimensioni dei grafi da realizzare. Nel caso bidimensionale i numeri sono della forma \(2^n \cdot 3^m\), con \(n, m \ge 0\) ed \(n + m \le 5\); in totale abbiamo bisogno di \(1 + 2 + 3 + \cdots + 6 = 21\) palline. Abbiamo anche bisogno di 15 stuzzicadenti rossi e altrettanti blu.
Nel caso tridimensionale i numeri sono della forma \(2^n \cdot 3^m \cdot 5^p\), con \(n, m, \ge 0\), \(n + m \le 4\), \(p \in \{0, 1, 2\}\); in totale abbiamo bisogno di \(3 \cdot (1 + 2 + 3 + 4 + 5) = 45\) palline. Ci servono anche 30 stuzzicadenti rossi, altrettanti blu e verdi. Naturalmente è opportuno avere palline e stuzzicadenti colorati di scorta per poter rimpiazzare quelli che si dovessero rompere o perdere durante la costruzione.
Il cartone deve essere di dimensione sufficiente ad accogliere i grafi e può essere tagliato in anticipo. Per stuzzicadenti di lunghezza 8–10 cm e grafi come quelli nelle fotografie è sufficiente un quadrato di lato 40–50 cm in entrambi i casi.
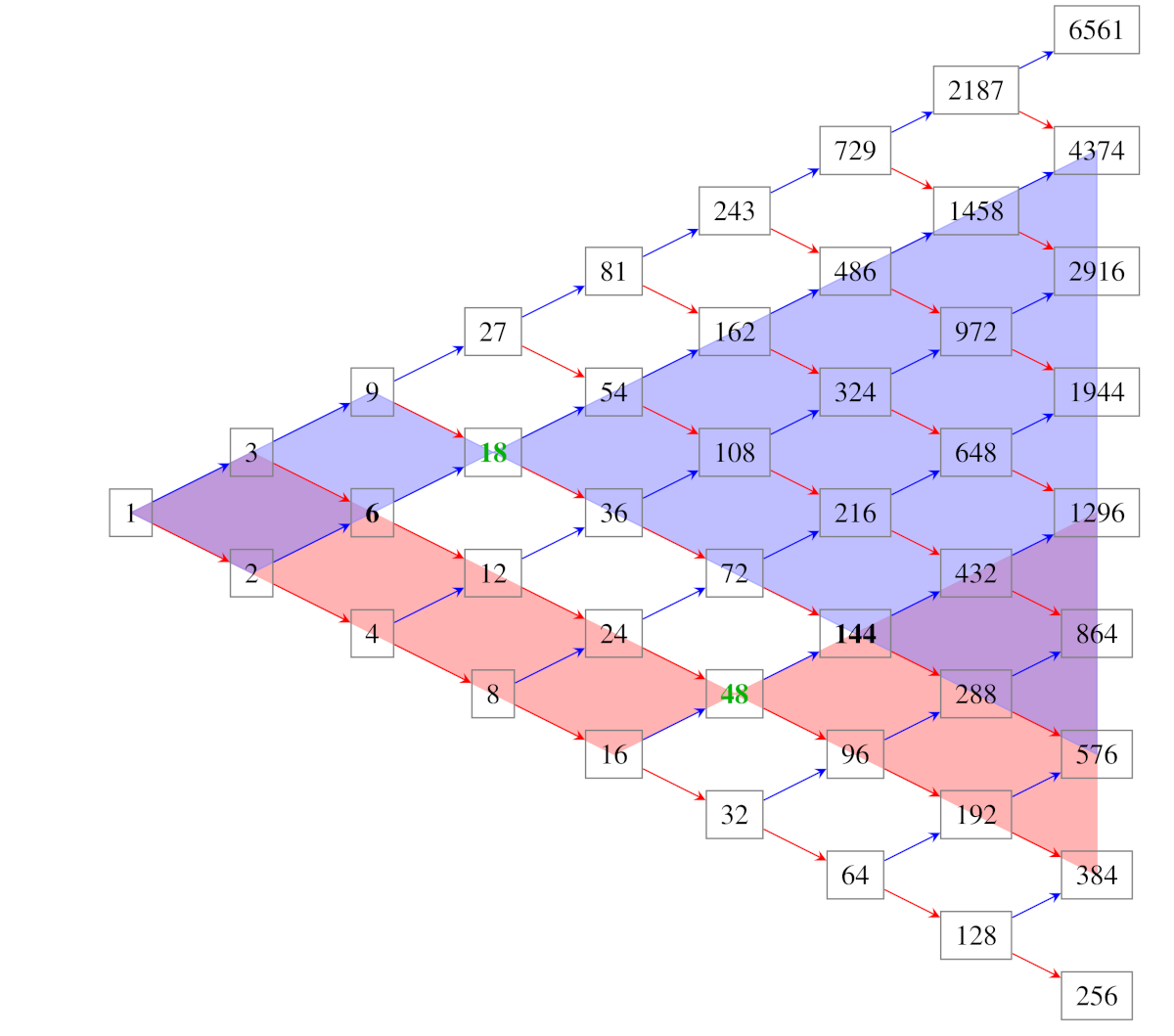
Il grafo bidimensionale con i numeri della forma \(2^n \cdot 3^m\), dove \(n\) ed \(m\) sono interi non negativi con \(n + m \le 8\). Il grafo realizzato in pratica è una parte di questo.
Realizzazione
Le due classi sono state mescolate e divise in due gruppi di circa 20–22 unità ciascuno; il primo gruppo ha realizzato il grafo bidimensionale, il secondo ha realizzato l’altro. I due gruppi si sono alternati fra il mio laboratorio e quello di Alberto Saracco sui ponti di Quackenberg (si veda anche il suo canale canale YouTube).
A ciascuno studente o studentessa è stata affidata una pallina o due, e ciascuno ha dovuto scrivere sulla pallina il numero corrispondente, seguendo i diagrammi nelle figure, che sono stati disegnati sulla lavagna durante la breve spiegazione preliminare che ha preceduto la fase di costruzione. Gli studenti sono poi stati chiamati in ordine e hanno dovuto sistemare le palline agganciandole alla struttura già parzialmente realizzata e aggiungendo i nuovi stuzzicadenti necessari per il passo successivo; di fatto ogni studente o studentessa ha mostrato ai due o tre successori come fare, sotto la supervisione dei docenti presenti.
Il grafo bidimensionale nella figura sopra è decisamente piú agevole da realizzare perché si possono appoggiare le palline direttamente sul cartone; volendo si può disegnare in anticipo sul cartone la posizione delle palline numerate e il colore degli stuzzicadenti che li collegano, per fare da guida.

Il grafo bidimensionale
Il grafo tridimensionale è stato realizzato a strati, seguendo lo schema dato nella figura qui sotto, partendo dal piano terra che è stato incollato sul cartone. Poi abbiamo piazzato gli stuzzicadenti verdi in verticale, uno su ciascuna pallina, e su questi abbiamo agganciato le palline del primo piano. Finito questo strato, abbiamo sistemato gli altri stuzzicadenti verdi in verticale sulle palline appena messe, e infine abbiamo realizzato il secondo piano. Avendo abbastanza tempo a disposizione, consigliamo di incollare la punta degli stuzzicadenti che devono comunque essere ben piantati nelle palline; l’esperienza mostra che spesso escono dalla loro sede mentre si sistemano le palline successive.
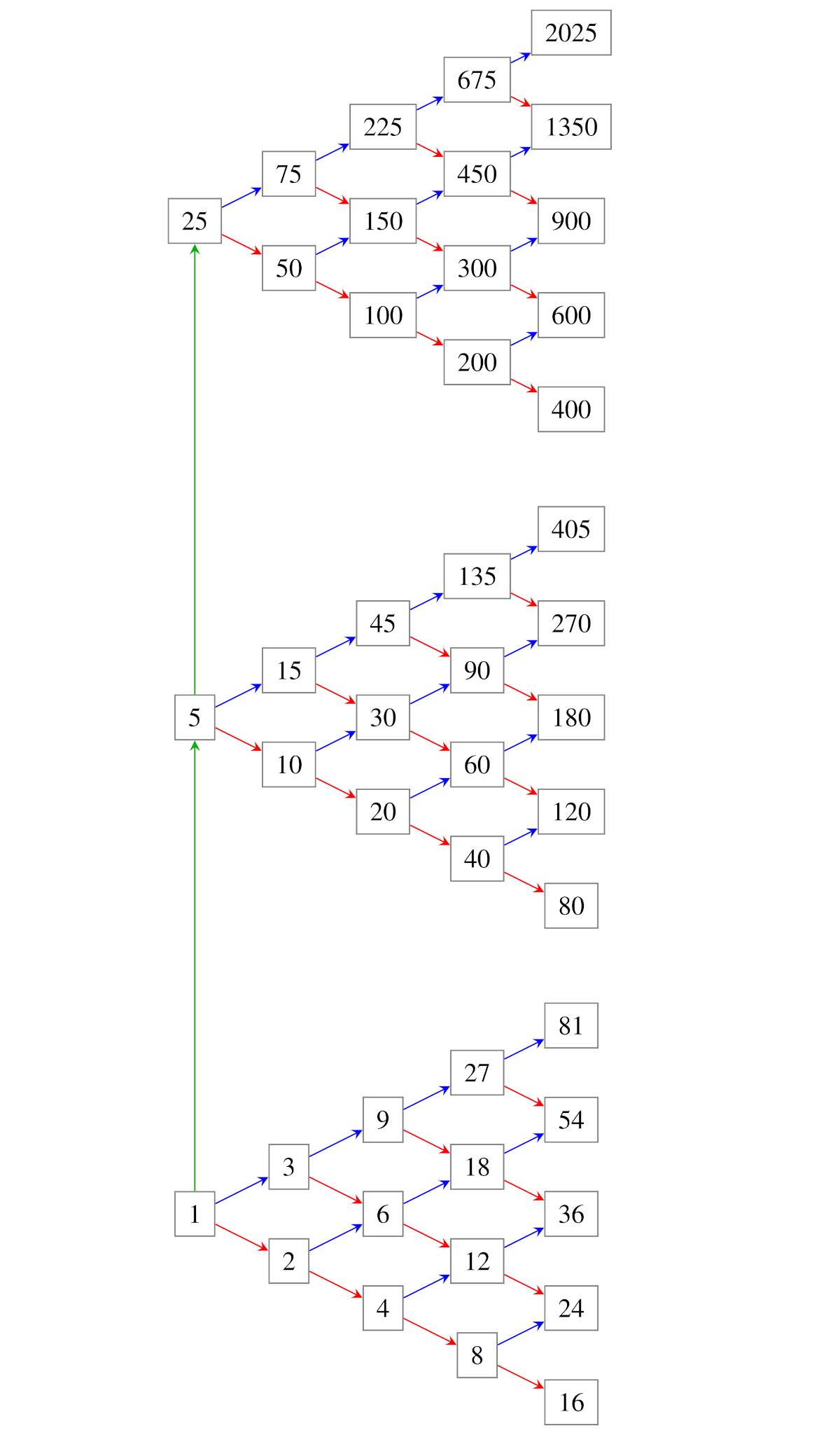
I tre livelli del grafo tridimensionale. Indichiamo solo gli archi verdi da 1 a 5 e da 5 a 25, ma ci sono anche tutti gli altri.

Una fase della costruzione del grafo tridimensionale
Analisi
Abbiamo usato gli oggetti costruiti per ricavare alcune informazioni di natura “teorica” sulla moltiplicazione. Tanto per cominciare, i divisori di un intero \(n\) sono resi ben visibili: sono semplicemente i vertici del grafo dai quali \(n\) è raggiungibile seguendo la direzione delle frecce. Per esempio, i divisori di 18 corrispondono alle palline nel parallelogramma di vertici opposti 1 e 18. Analogamente, i multipli di \(n\) sono gli interi che si possono raggiungere da \(n\) seguendo le frecce, cioè quelli nell’angolo rivolto verso destra che ha un vertice in \(n\). Nella figura, divisori e multipli di 18 e di 48 sono indicati dallo sfondo colorato.
Il grafo mostra anche la proprietà commutativa della moltiplicazione e alcune proprietà delle potenze: per esempio \((2^a \cdot 3^b) \cdot (2^\alpha \cdot 3^\beta) =
2^{a + \alpha} \cdot 3^{b + \beta} =
(2^\alpha \cdot 3^\beta) \cdot (2^a \cdot 3^b)\), perché dal numero \(n = 2^a \cdot 3^b\) si può raggiungere il numero \(n m = 2^{a + \alpha} \cdot 3^{b + \beta}\) dove \(m = 2^\alpha \cdot 3^\beta\) e viceversa, percorrendo il numero opportuno di archi di ogni colore.
Per quanto riguarda l’unicità della fattorizzazione, facendo riferimento per semplicità alla prima figura, è possibile raggiungere il numero 288 partendo da 1 in tanti modi, ma qualunque sia la scelta che facciamo percorriamo 5 archi rossi e 2 archi blu. Naturalmente questo fatto vale anche per il grafo tridimensionale, come si può facilmente verificare, e in generale per tutti i numeri naturali.
I grafi rendono ben visibili i concetti di massimo comun divisore e minimo comune multiplo, che sono il piú grande predecessore e il piú piccolo successore comune. Illustriamo questa proprietà mediante i numeri indicati in verde nella prima figura, gli interi 18 e 48; in grassetto il loro massimo comun divisore 6 e minimo comune multiplo 144. Il fondo colorato indica multipli e divisori degli interi in esame che sono, come si diceva sopra, i numeri raggiungibili e, rispettivamente, i numeri dai quali si possono raggiungere. Dunque il massimo comun divisore si trova all’intersezione delle aree colorate nella figura (i parallelogrammi di vertici opposti 1 e 18, e 1 e 48 rispettivamente) e analogamente il minimo comune multiplo si trova all’intersezione degli angoli colorati che hanno vertice in 18 e 48.
È anche molto facile giustificare le due “regole” che permettono il calcolo di queste quantità a partire dalla scomposizione in fattori primi. Limitandoci ancora al caso bidimensionale, se \(n = 2^a \cdot 3^b\) ed \(m = 2^\alpha \cdot 3^\beta\) allora li si può raggiungere entrambi dal numero \(2^{\min(a, \alpha)} \cdot 3^{\min(b, \beta)}\) e da nessun intero piú grande; viceversa, da entrambi si può raggiungere il numero \(2^{\max(a, \alpha)} \cdot 3^{\max(b, \beta)}\) e nessun numero piú piccolo ha questa proprietà.
Concludiamo osservando che è possibile leggere dal grafo anche qualche informazione aritmetica piú sofisticata. Il numero dei colori diversi che usiamo per raggiungere un intero è uguale al numero dei suoi fattori primi distinti. Il numero degli stuzzicadenti (eventualmente dello stesso colore) che percorriamo per raggiungere un intero è uguale al numero totale dei suoi fattori primi. La formula per il numero dei divisori di un intero può essere “indovinata” dal grafo. Per esempio, 18 ha 6 divisori perché il parallelogramma di vertici opposti 1 e 18 ha 2 palline su un lato e 3 sull’altro. In generale, il numero \(2^a \cdot 3^b\) ha \((a + 1)(b + 1)\) divisori. Mutatis mutandis, la cosa, vale naturalmente anche per il grafo tridimensionale e in realtà per qualunque numero di fattori primi distinti.
Alla fine si possono lasciare alcune domande. Perché sul grafo tridimensionale non compaiono tutti i numeri naturali? Aggiungendo altre “dimensioni” sarebbe possibile raggiungere proprio tutti i numeri naturali? Basta un numero finito di colori, cioè di numeri primi, per raggiungere tutti i numeri? In altre parole, i numeri primi sono finiti o infiniti? Il fatto che i numeri raggiunti sono relativamente poco “densi” suggerisce che un qualunque insieme finito di numeri primi non è sufficiente a generare tutti gli interi, suggerendo la validità del Teorema di Euclide per il quale esistono infiniti numeri primi. Questa intuizione può essere formalizzata per darne una dimostrazione rigorosa: si veda la sesta puntata della mia mini-serie sull’esistenza di infiniti numeri primi[4 ]A. Zaccagnini. “\(\exists\infty\#p!\) La Serie!” Sito Web MaddMaths! https://maddmaths.simai.eu/in-evidenza/primi-0/. (2021) e la versione su YouTube [5 ]A. Zaccagnini. “\(\exists\infty\#p!\) La Serie!” Playlist (2021).
Conclusioni e ringraziamenti
In conclusione, è forse piú comodo usare palline di polistirolo piú grandi; avendo tempo a disposizione, conviene incollare le punte degli stuzzicadenti in modo che non escano piú dalle palline in cui sono conficcati. Inoltre è opportuno trovare un modo per riempire i tempi morti che ci sono stati perché alla costruzione materiale del grafo partecipano solo due o tre studenti alla volta; ho provato a riempirli con le spiegazioni “teoriche” ma non si può dire che ci sia riuscito molto bene.
Ringrazio le docenti Maria Chiara Gullo e Lorenza Serventi, e tutti i ragazzi e le ragazze che hanno partecipato a questo laboratorio con entusiasmo. Ringrazio MaddMaths! che ancora una volta ospita un mio intervento. In particolare ringrazio Roberto Natalini, rivelando un piccolo retroscena: questo laboratorio deriva in gran parte dalle idee presentate nell’articolo [6 ]A. Zaccagnini. “Operazioni: Elementari, Ma Non Troppo!” Sito Web MaddMaths! https://maddmaths.simai.eu/divulgazione/focus/operazioni-elementari/ (2020). che è nato proprio da una chiacchierata con lui, quasi cinque anni fa.
Note e riferimenti
| ⇧1 | A. Zaccagnini. “I Gioielli Della Matematica.” Sito Web MaddMaths! https://maddmaths.simai.eu/didattica/i-gioielli-della-matematica/. (2024) |
|---|---|
| ⇧2 | C. Cozzani, R. Sandri e A. Zaccagnini. “Collane, Orecchini E Scatolette — Costruzione Di Oggetti Matematici Con Materiali Della Vita Quotidiana.” Archimede 1: 2–19 (2024). |
| ⇧3, ⇧6 | A. Zaccagnini. “Operazioni: Elementari, Ma Non Troppo!” Sito Web MaddMaths! https://maddmaths.simai.eu/divulgazione/focus/operazioni-elementari/ (2020). |
| ⇧4 | A. Zaccagnini. “\(\exists\infty\#p!\) La Serie!” Sito Web MaddMaths! https://maddmaths.simai.eu/in-evidenza/primi-0/. (2021) |
| ⇧5 | A. Zaccagnini. “\(\exists\infty\#p!\) La Serie!” Playlist (2021) |