In questo post inseriamo il materiale complementare all’articolo “Logica e problemi medioevali con l’aiuto di circuiti logici e qualche spunto per l’uso di Arduino“ scritto da Francesca Leoncini e Davide Passaro pubblicato sul numero 1 del 2020 della rivista Archimede (disponibile a pagamento qui). In questo articolo sono presentati degli spunti spunti didattici finalizzati a realizzare percorsi sulla logica nel primo biennio di un liceo.
Tra i molteplici approcci, in quell’articolo è mostrata una proposta che evidenzia il fondamentale ruolo della logica nei circuiti. In particolare è presentata un’esperienza realizzata in una classe dell’indirizzo matematico del Liceo Statale Alessandro Volta di Colle di Val d’Elsa (SI). Sempre in quel testo sono mostrati alcuni spunti inerenti all’utilizzo della piattaforma hardware dotata di microcontrollore Arduino e inserite alcune considerazioni didattiche relative alle proposte presentate. In questo post è inserito il materiale complementare all’articolo.
In particolare :
- Problemi e soluzioni aggiuntive proposte agli studenti
- Link al sofwtare di progettazione di circuiti e schemi di circuiti realizzati
- Link a tutorial per iniziare ad utilizzare Arduino ed esempi utili di progetti realizzati
Problemi e soluzioni aggiuntive proposte dagli studenti
Il percorso didattico, descritto più dettagliatamente nell’articolo, ha preso il via dall’analisi di problemi ludici: la matematica ricreativa costituisce infatti il filo conduttore delle attività proposte.
Sono stati affrontati diversi problemi estratti dal testo di R. M. Smullyan, « What Is the Name of This Book?» , e la loro risoluzione è passata, oltre che per l’approccio intuitivo, attraverso la costruzione di formule logiche e la rappresentazione delle corrispondenti tavole di verità. Nell’articolo viene presentata in maniera completa questa modalità di risoluzione relativamente al problema 28 del testo di Smullyan (cfr. Problema 1 nell’articolo pubblicato su Archimede), che costituisce un semplice esempio allo scopo di familiarizzare con la formalizzazione e la procedura.
Nell’articolo vengono presentati il Problema 2 (cfr. problema 29 nel testo di Smullyan) e il Problema 3 (variazione del precedente) le cui corrispondenti tavole di verità vengono riportate di seguito.
Problema 2 (S-29). Anna e Bruno sono due abitanti dell’isola dei cavalieri e dei furfanti. Anna afferma: “Io sono un furfante o Bruno è un cavaliere”. Qual è la natura di Anna e di Bruno?
Problema 3. Anna e Bruno sono due abitanti dell’isola dei cavalieri e dei furfanti. Anna afferma: “Io sono un cavaliere o Bruno è un furfante”. Qual è la natura di Anna e di Bruno?
Qui si schematizzano brevemente il ragionamento e la codifica utilizzati per la risoluzione dei problemi ambientati nella nota Isola di Smullyan, l’isola in cui ciascun abitante o è sempre sincero o mente sempre.
- Ogni abitante dell’isola viene indicato con una lettera maiuscola (come A per Andrea).
- Con la corrispondente lettera minuscola si indica la proposizione atomica che afferma la natura sincera del personaggio, cioè \( a\) rappresenta la proposizione “Andrea è un cavaliere”, mentre \( \overline a \) ne rappresenta la negazione, cioè l’affermazione “Andrea è un furfante”.
- Con la corrispondente lettera dell’alfabeto greco viene indicata la proposizione logica che traduce l’affermazione del personaggio.
Nelle tabelle seguenti, le righe colorate in verde rappresentano le soluzioni relative ai problemi.
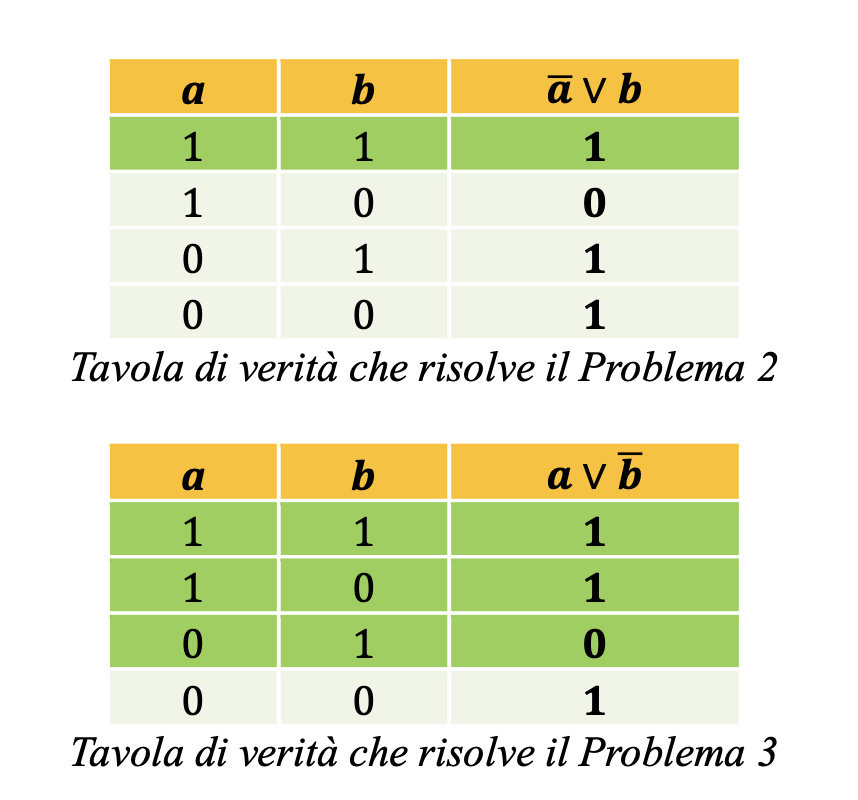
L’evidente somiglianza nella struttura verbale dei due problemi analizzati sopra non solo non si rintraccia in alcuna forma di commutatività delle soluzioni, ma nemmeno si mantiene nell’univocità delle soluzioni stesse: ci sono ben tre configurazioni che soddisfano il Problema 3.
I suddetti due problemi, presentati uno di seguito all’altro, costituiscono una valida occasione per insinuare un’attenzione particolare alle affermazioni autoreferenziali.
Nell’ottica di affrontare problemi di complessità crescente, se ne presentano qui altri due estratti dal testo di Smullyan.
Problema S-31. Anna, Bruno e Chiara sono tre abitanti dell’isola dei cavalieri e dei furfanti. Anna afferma: “Siamo tutti furfanti”. Bruno afferma: “Esattamente uno di noi è un cavaliere” Qual è la natura dei tre abitanti?
Problema S-32. Anna, Bruno e Chiara sono tre abitanti dell’isola dei cavalieri e dei furfanti. Anna afferma: “Siamo tutti furfanti”. Bruno afferma: “Esattamente uno di noi è un furfante” Qual è la natura dei tre abitanti?
Nei seguenti schemi di risoluzione dei problemi, ciascuna tavola di verità è preceduta dalle proposizioni logiche in cui sono state tradotte le affermazioni dei protagonisti.
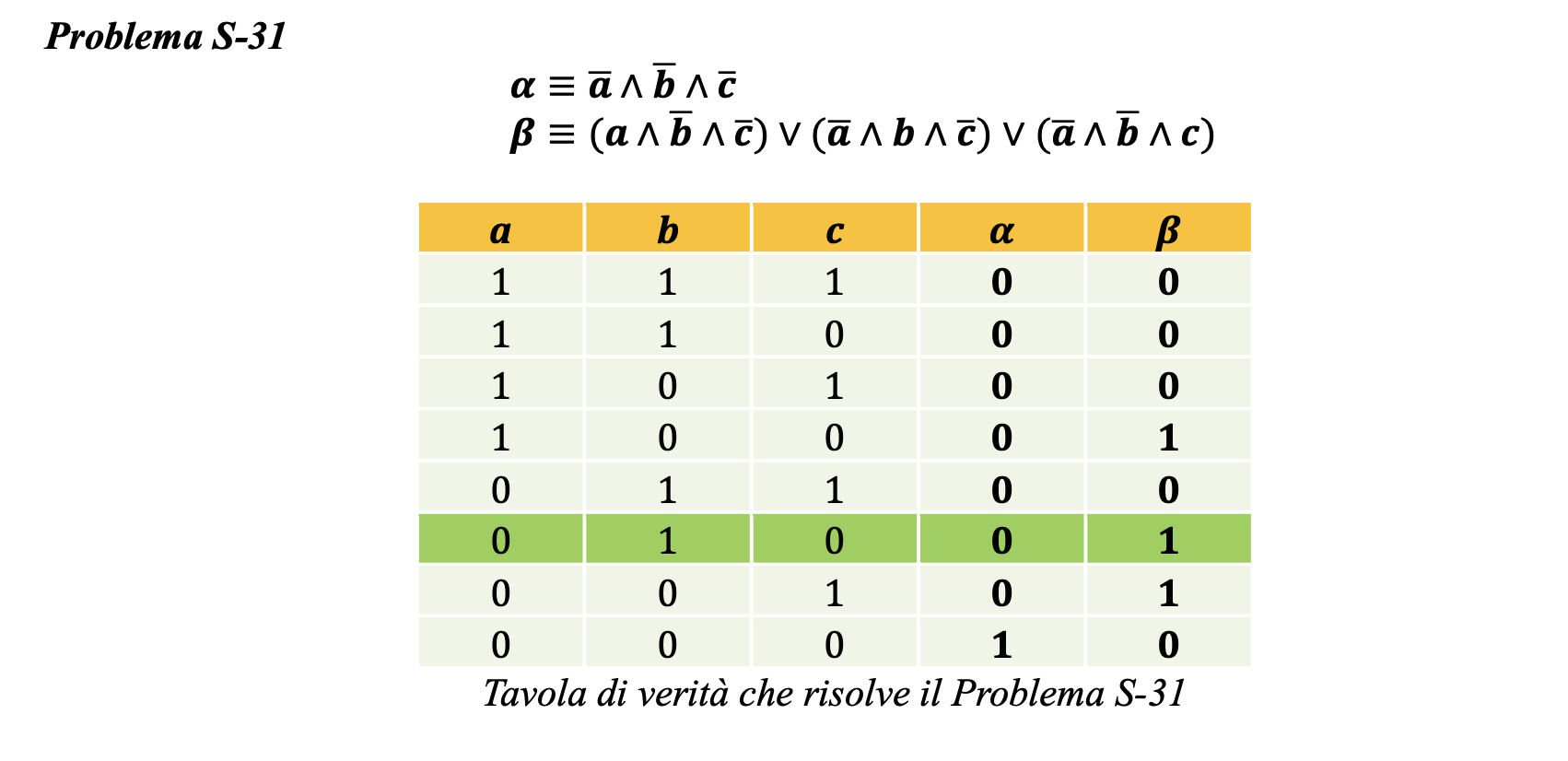
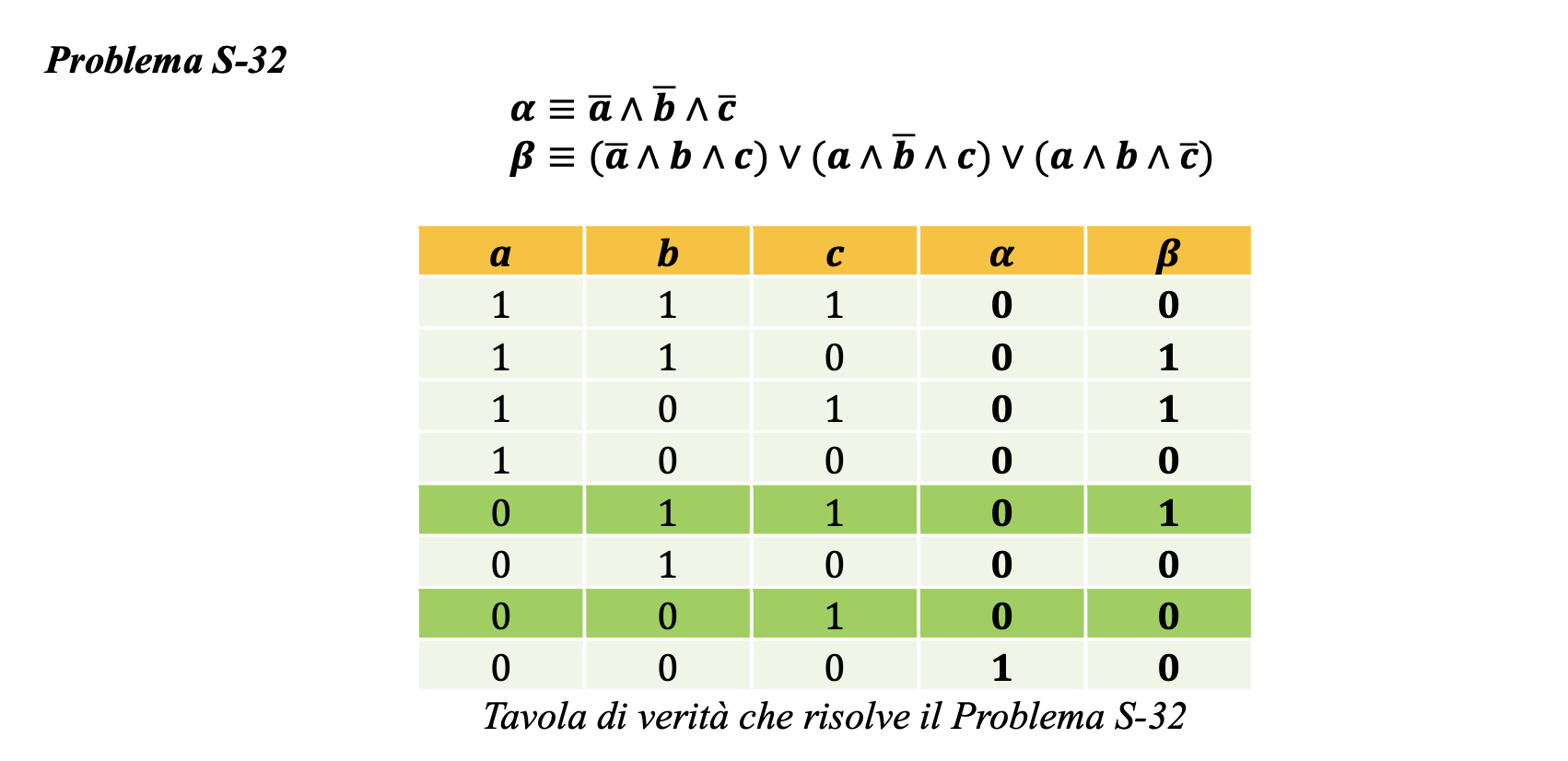
Si può osservare che i due problemi differiscono per un singolo dettaglio nell’affermazione di Bruno. Le soluzioni, invece, differiscono in modo significativo relativamente al loro numero, come si rileva dalle tavole di verità che risolvono i problemi. Di nuovo, si evidenzia l’importanza di una riflessione particolare sulle affermazioni negative e autoreferenziali.
Info sul software di progettazione di circuiti e schemi di circuiti realizzati
Nell’articolo si cita l’uso del software Logisim (http://www.cburch.com/logisim/), un simulatore virtuale di circuiti logici, estremamente utile per rappresentare reti logiche prima della costruzione concreta di circuiti logici o in alternativa ad essa.
Il software può essere inoltre utilizzato per verificare l’equivalenza logica tra diverse proposizioni logiche. Nel seguente schema (cfr. Figura 1), realizzato con Logisim, è rappresentato il circuito logico che testa la validità di entrambe le leggi di De Morgan.
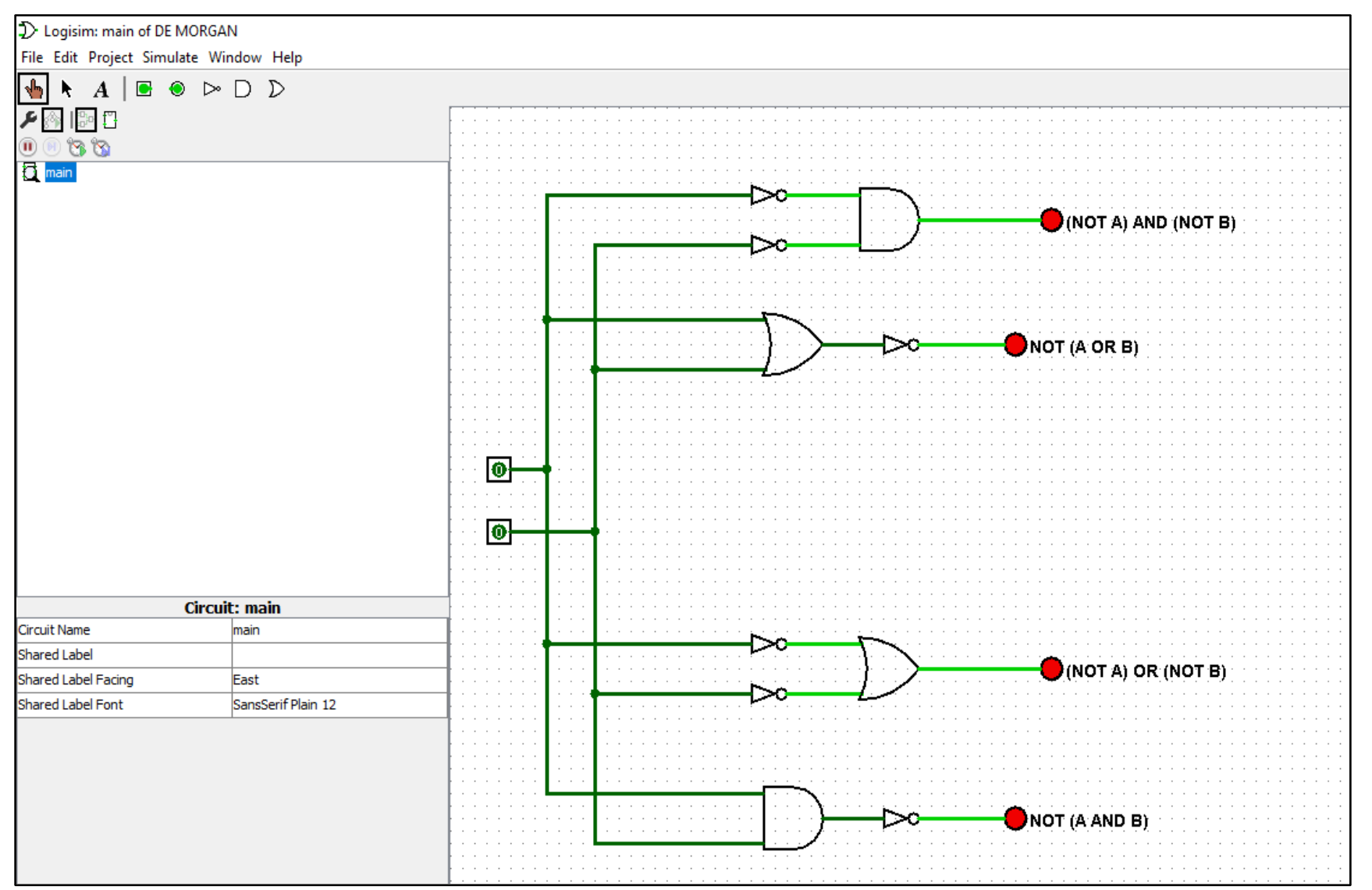
Figura 1: rete logica che verifica le leggi di De Morgan, realizzata con LogiSim
Nel percorso didattico riportato nell’articolo, vengono affrontati due dei cosiddetti problemi di attraversamento di Alcuino di York (tradotti dal latino, con testo originale a fronte, da R. Franci nei “Giochi matematici alla corte di Carlomagno – Problemi per rendere acuta la mente dei giovani”).
Problema 4 (AY-18). Un uomo deve trasportare al di là di un fiume un lupo, una capra e un cavolo. L’uomo ha a disposizione una barchetta con cui ne può trasportare solo uno alla volta. Come può trasferirli indenni?
Problema 5 (AY-17). Tre ragazzi hanno ciascuno una sorella e ognuno di essi desidera la sorella degli altri due. Tutti devono attraversare un fiume avendo a disposizione una barchetta che può trasportare solo due di loro alla volta. In quale modo possono fare l’attraversamento senza che nessuna ragazza venga oltraggiata?
Questi problemi sono stati affrontati con l’obiettivo di realizzare un allarme che si attivi quando si verifica una delle situazioni di pericolo che devono essere evitate.
Relativamente al Problema 4 (cfr. propositio 18 nel testo di Alcuino di York), nell’articolo viene descritta la costruzione del circuito che implementa la rete logica in grado di realizzare l’allarme per un attraversamento in sicurezza di ‘lupo, capra e cavolo’.
La proposizione che adempie a questo scopo può essere espressa in due modalità equivalenti che vengono riportate di seguito (cfr. Figura 2). Gli input da gestire sono tre (o quattro) corrispondenti ai protagonisti della storia; i valori di verità assunti dagli input dipendono dalla rispettiva presenza (1) o assenza (0) del corrispondente personaggio sulla sponda del fiume presa in esame.
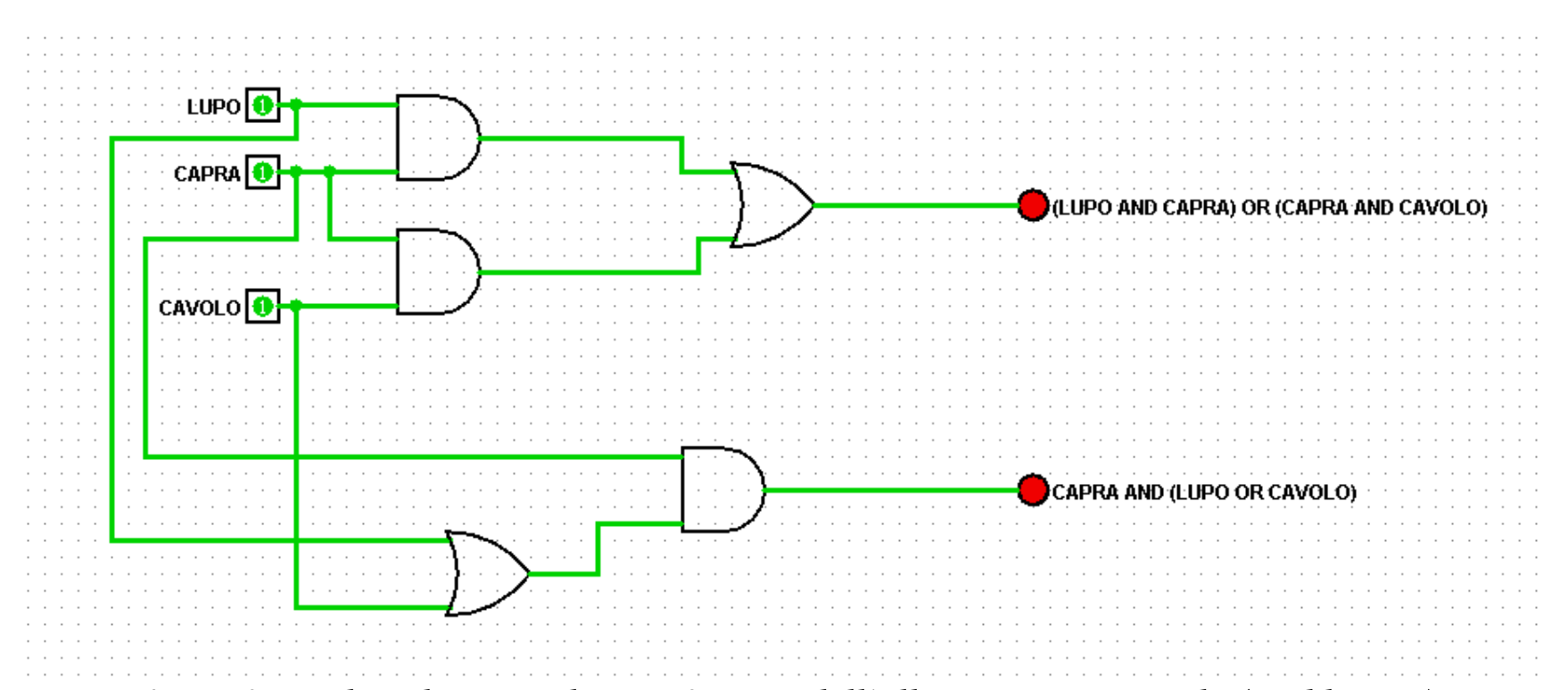
Figura 2: reti logiche equivalenti, a 3 input, dell’allarme su una sponda (Problema 4)
Nel seguente schema (cfr. Figura 3) realizzato con Logisim, vengono considerati quattro input: oltre al lupo, alla capra e al cavolo, si aggiunge anche l’input dell’uomo (indicato come ‘pastore’) che ricopre i ruoli di traghettatore e guardiano.
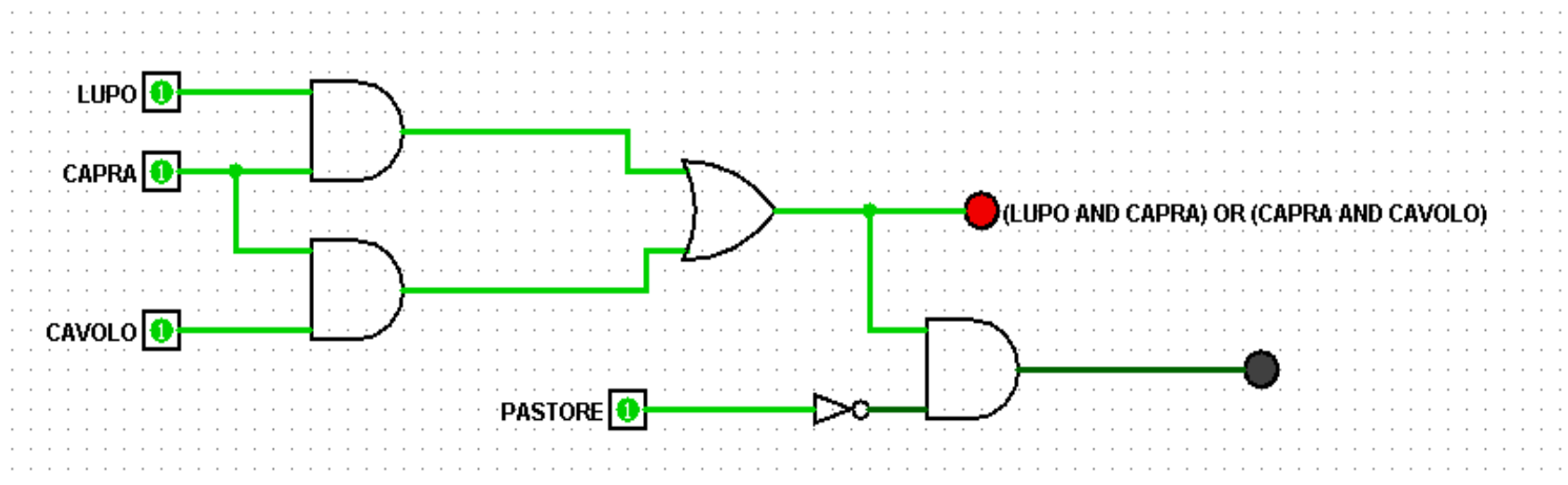
Figura 3: rete logica, a 4 input, dell’allarme su una sponda (Problema 4)
La metodologia didattica ha previsto l’intervento costante degli studenti, i cui contributi hanno condotto ad un ampliamento della complessità e della completezza della situazione affrontata. In particolare, l’individuazione di due reti equivalenti (ottimizzazione del circuito) e l’aggiunta della figura del pastore discendono da osservazioni e suggerimenti degli allievi stessi.
Un’ulteriore proposta prende in considerazione la situazione di pericolo che si può avere su entrambe le sponde del fiume (cfr. Figura 4). Alla versione presentata di seguito si è arrivati procedendo per passaggi via via più raffinati e precisi.
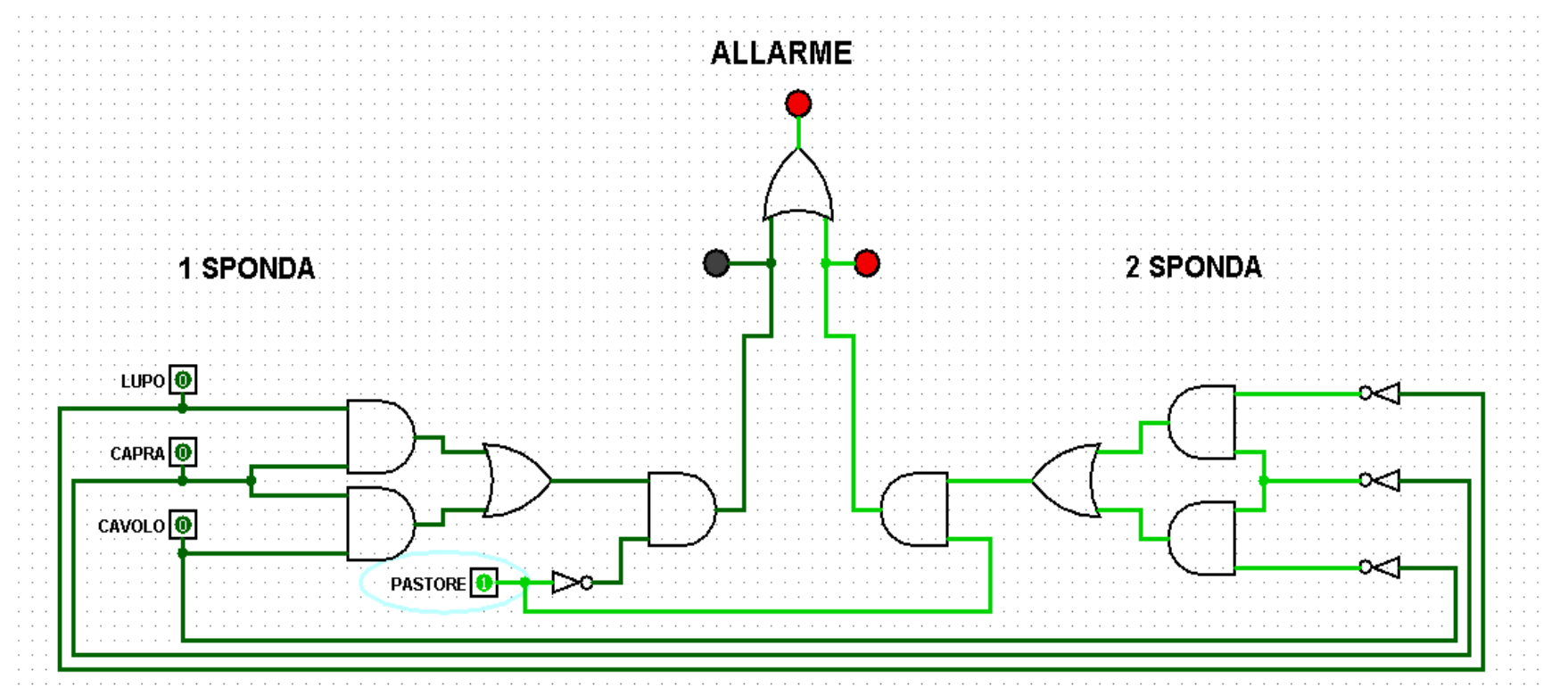
Figura 4: rete logica, a 4 input, degli allarmi sulle due sponde (Problema 4)
Relativamente al Problema 5 (cfr. propositio 17 nel testo di Alcuino di York), si richiede l’attraversamento del fiume da parte dei sei protagonisti costituiti da tre coppie fratello-sorella, col solito vincolo di due soggetti alla volta, evitando che alcuna ragazza resti in compagnia di un ragazzo senza la presenza del proprio fratello. Anche in questo caso si pone il compito di realizzare un allarme che si attivi nei casi in cui almeno una delle ragazze rischia la proprià integrità. Stavolta gli input da gestire sono ben sei e per comodità di rappresentazione, viene dato nome ai personaggi delle tre coppie formate da fratello e sorella: Andrea (A) e Anna (a), Bruno (B) e Barbara (b), Carlo (C) e Chiara (c). Le lettere tra parentesi indicano le proposizioni logiche atomiche corrispondenti ai personaggi e i cui valori di verità dipendono dalla loro rispettiva presenza (1) o assenza (0) sulla sponda presa in esame. L’allarme richiesto può essere realizzato attraverso la seguente proposizione logica:
![]()
che viene implementata dalla seguente rete logica (cfr. Figura 5).
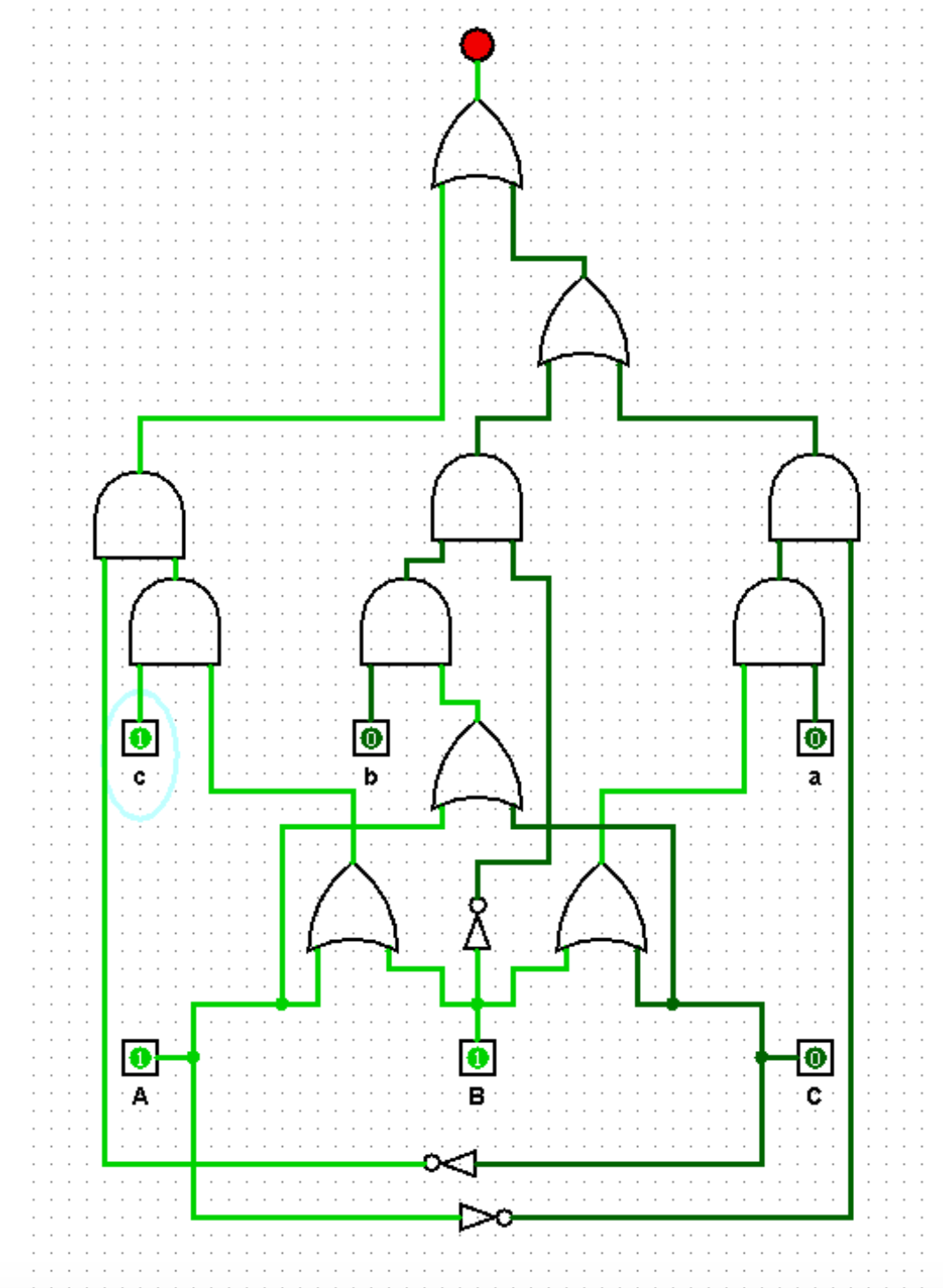
Figura 5: rete logica, a 6 input, dell’allarme su una sponda (Problema 5)
Questa rete logica può essere ottimizzata e la sua implementazione fisica in un circuito logico reale non è stata realizzata.
Sono invece stati costruiti i circuiti logici (cfr. Figura 6) su basette breadboard che implementano le varie reti logiche relative ai diversi sistemi di allarme per il Problema 4.
Si segnala che per la realizzazione fisica dei circuiti logici, i costi sono stati estremamente contenuti, dal momento che sono stati utilizzati molti materiali di recupero, come cavi e LED provenienti da PC dismessi, caricabatterie di vecchi cellulari e strumenti già in dotazione al laboratorio di fisica, come resistenze e multimetro. Sono state acquistate espressamente per la realizzazione di questa parte del percorso didattico solo le basette breadboard: esse costituiscono il supporto fisico su cui realizzare il circuito. Queste hanno costi contenuti (con poche decine di euro se ne acquistano per una intera classe suddivisa in piccoli gruppi) e sono facilmente reperibili anche online.

Figura 6: circuito logico che implementa le due reti equivalenti rappresentate in Figura 2
Link a tutorial sull’uso di Arduino
Da qualche anno si è ormai diffuso l’uso del microcontrollore Arduino sia fra i cosiddetti “artigiani digitali” (più conosciuti con il termine inglese di “Makers“) sia in un’ampia comunità di persone che comprende anche studenti e docenti. La facilità dell’utilizzo di Arduino è supportata proprio dai tanti utenti che condividono in rete in modo gratuito progetti e guide per l’utilizzo.
Arduino, infatti, è una scheda in grado di interpretare i segnali provenienti da sensori (termometri, interruttori, fotocellule, sensori di infrarossi, rilevatori di ultrasuoni, ecc.) e di azionare degli attuatori (luci, avvisatori acustici, motorini elettrici, relè, display, ecc.) sulla base di un programma che interpreta i segnali dei sensori e li elabora, decidendo se, come e quali attuatori attivare. Arduino unisce quindi due mondi: quello hardware, rappresentato dalla scheda e dai componenti elettronici ad essa collegabili e quello software, rappresentato dal programma scritto separa- tamente su un computer e successivamente caricato su Arduino.
Esistono in commercio anche dei kit (chiamati «starter kit») che vengono venduti insieme con tutto l’occorrente per realizzare semplici progetti (accendere un led, utilizzare un sensore di luce, mettere in moto un motore, ecc…).
Per questi motivi, Arduino ben si presta ad essere utilizzato nelle classi di liceo (l’utilizzo in altri tipi di scuola come gli istituti tecnici ovviamente si considera scontato e già ampiamente diffuso) all’interno di discipline come la matematica e la fisica anche sfruttando, consapevoli delle limitazioni orarie a cui sono sottoposti docenti e studenti, la possibilità di progetti pomeridiani o appunto di sperimentazioni quali quelle del Liceo Matematico.
Tra le tante possibili guide che si trovano a partire dai motori di ricerca segnaliamo:
- Gli esempi guidati proposti dal sito ufficiale di Arduino
- Questa guida del sito HTML
Molto diffusi sono anche video di spiegazione caricati su YouTube. Vi invitiamo a cercare quello che più vi sembra adatto anche in base alle vostre competenze.
Qui di seguito ne inseriamo uno di esempio.






![Problemi di matematica e come "disegnarli" Low-Res_animaux[41]](https://maddmaths.simai.eu/wp-content/uploads/2024/03/Low-Res_animaux41-300x300.jpg)












