Una nuova mini-serie, fatta di video e articoli, di Alessandro Zaccagnini, matematico, esperto di teoria dei numeri, autore del Dialogo sui numeri primi. Questa volta si fa accompagnare da una tartaruga per raccontarci cosa sono le somme esponenziali e perché sono tanto utili nella sua disciplina. Questa è la terza puntata. Tutte le puntate le trovate su questa pagina.

Angoli “irrazionali”

Rotazione di un angolo irrazionaleSe prendiamo un angolo in rapporto irrazionale con l’angolo giro la successione dei vettori non è piú periodica e le somme (cioè i vettori neri) non passano da 0, ma la somma resta limitata, come si dimostra usando la formula per la somma di progressioni geometriche che abbiamo visto nella seconda puntata. Per fare un esempio concreto, prendiamo \(\alpha = \sqrt{2}\) e \(q = \mathrm{e}^{2 \pi \mathrm{i}\alpha}\). Dunque, usando la formula citata con \(x = q\) ed \(m\) qualsiasi troviamo a destra una frazione il cui numeratore ha valore assoluto che non supera 2, per la disuguaglianza triangolare, e il denominatore \(1 – q\) ha valore assoluto fissato e diverso da 0.

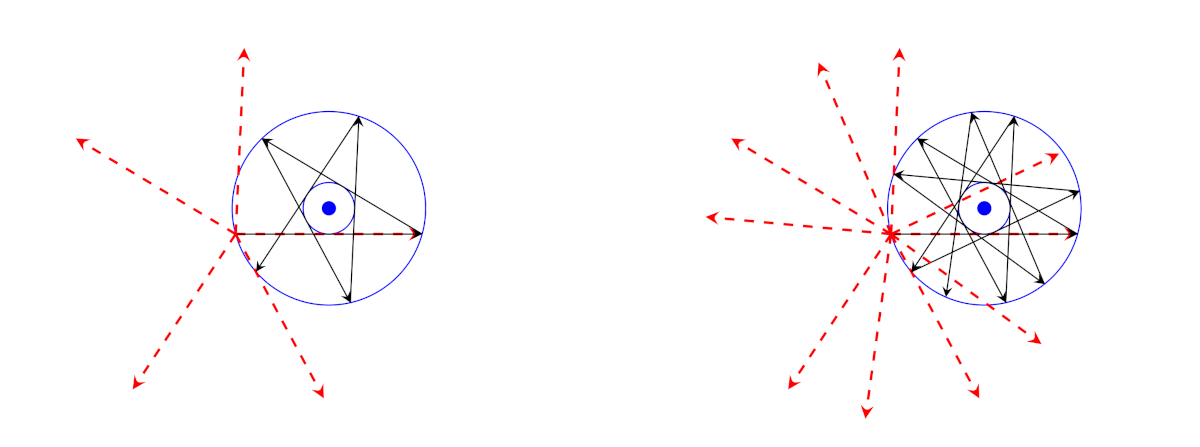
La figura della copertina di questa puntata illustra meglio delle mie parole quello che succede: vediamo i primi 5 o 10 vettori che si ottengono con \(\alpha = \sqrt{2}\). Sono indicate la circonferenza su cui giacciono le estremità dei vettori neri la circonferenza tangente a questi ultimi. L’immagine a sinistra somiglia al poligono intrecciato con \(n = 5\) della copertina della seconda puntata perché ruotiamo di \(\sqrt{2}\) volte un angolo giro, cioè \(\approx 509.12^\circ\), cioè un angolo giro piú \(149.12^\circ\), mentre nel pentagono intrecciato ruotiamo di \(2 \cdot 72^\circ = 144^\circ\).

Utilizzando ancora la formula per la somma di una progressione geometrica vista nella seconda puntata e qualche identità trigonometrica possiamo dimostrare che le punte dei vettori neri si trovano sulla circonferenza di centro \[\Bigl( \frac12, \frac{1 + \cos(\alpha)}{2 \sin(\alpha)} \Bigr)
=
\Bigl(\frac12, \frac12 \mathrm{cotg}\bigl( \frac12 \alpha \bigr) \Bigr)\] e raggio \(1 / (2 \sin (\alpha / 2))\). Tutti questi vettori sono tangenti alla circonferenza con lo stesso centro e raggio \(\frac12 \mathrm{cotg}(\alpha / 2)\). Lo stesso accade anche nei casi trattati nelle puntate precedenti, in cui se ricordate abbiamo sempre indicato il centro del poligono che è anche il centro delle due circonferenze, anche se la cosa non colpisce l’occhio in modo particolare come succede in questo caso.

Ci sono alcune osservazioni da fare per spiegare le differenze tra questo caso e quelli descritti nelle puntate precedenti.

La tartaruga del logo non torna mai alla posizione di partenza, cioè nell’origine, ma non si allontana piú di tanto, come abbiamo appena visto. Però si può dimostrare che passa arbitrariamente vicina all’origine. C’è una parte della Teoria dei Numeri, che si chiama approssimazione diofantea, che ci garantisce che per infiniti interi \(N\) il numero \(N \sqrt{2}\) è molto vicino ad un intero e quindi \(q^N = \mathrm{e}^{2 \pi \mathrm{i}N \sqrt{2}}\) è molto vicino ad 1 e il numeratore della frazione a destra nella formula della seconda puntata è molto vicino a 0 quando \(m + 1 = N\).

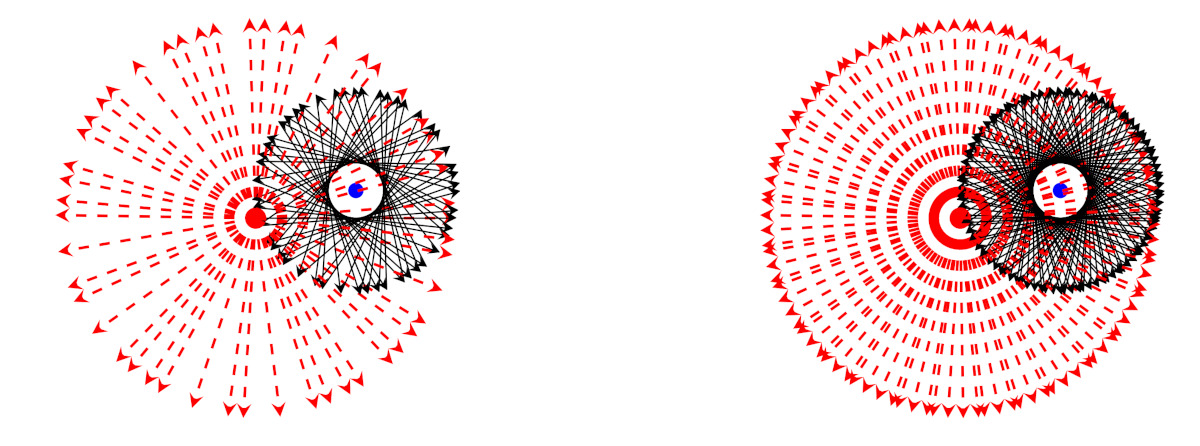
In rosso, a sinistra i primi 50 termini della successione con \(\alpha = \sqrt{2}\), a destra i primi 100; in nero le relative somme.

Quando ruotiamo i vettori di angoli in rapporto razionale con l’angolo giro la successione che otteniamo è periodica e gli stessi vettori si ripetono. La situazione illustrata nelle figure qui sopra è radicalmente diversa. Non solo i vettori rossi non si ripetono, ma tendono a distribuirsi in modo da occupare tutto lo spazio a disposizione, senza concentrarsi in alcune direzioni particolari, come succede nel caso trattato nelle prime due puntate. Senza dare una definizione formale, le illustrazioni di questa puntata danno un’idea abbastanza precisa del concetto di “uniforme distribuzione modulo 1.”

Per disegnare le figure possiamo riutilizzare la funzione poligono definita nella scorsa puntata; per esempio otteniamo la seconda con il comando poligono 200 149.12 100.

Riassumendo, le somme esponenziali che abbiamo visto fin qui sono espressioni del tipo \[\sum_{n = 0}^N \mathrm{e}^{2 \pi \mathrm{i}f(n)}\] dove \(f(n) = \alpha n\), per vari valori di \(\alpha\); in altre parole, \(f\) è un monomio di primo grado. Abbiamo visto, e sostanzialmente dimostrato, che se \(\alpha\) è un numero razionale fissato \(\frac aq\) ridotto ai minimi termini e con \(q \ge 2\) allora la somma con \(N = q – 1\) vale 0 e quindi la somma con un numero arbitrario di termini \(N\) è periodica. Se \(a = 1\) troviamo i poligoni regolari che abbiamo visto nella prima puntata, mentre se \(a \ne 1\) (piú precisamente, se \(a \not\equiv 1 \bmod q\)) allora troviamo dei poligoni intrecciati come quelli della seconda puntata. Se \(\alpha\) è irrazionale la somma non vale mai 0, ma è in ogni caso limitata, cioè non esce da una circonferenza opportuna, di cui abbiamo calcolato centro e raggio.

Nelle prossime puntate prenderemo come funzione \(f\) un monomio di secondo o di terzo grado, e le cose cambieranno radicalmente.

Torniamo per un istante all’uniforme distribuzione: c’è un importante criterio dovuto ad Hermann Weyl, valido per una successione qualsiasi \(f\). In poche parole, la successione \(f\) è uniformemente distribuita se la somma esponenziale con \(m f(n)\) al posto di \(f(n)\) è “piccola” per ogni intero \(m \ne 0\). Questo criterio spiega perché il caso \(\alpha\) razionale è cosí diverso dal caso \(\alpha\) irrazionale. Infatti, se \(\alpha\) è il numero razionale \(\frac aq\), allora quando \(m = q\) i valori \(\mathrm{e}^{2 \pi \mathrm{i}m f(n)}\) sono tutti uguali ad 1 perché \(m f(n) = a n\) è un numero intero, e di conseguenza la somma esponenziale con questo valore di \(m\) non è piccola. Se invece \(\alpha\) è irrazionale, come nel caso di \(\sqrt{2}\), allora anche \(m \alpha\) è irrazionale, in particolare non è intero, per ogni intero \(m\) diverso da zero. Questo significa che i vettori \(\mathrm{e}^{2 \pi \mathrm{i}m f(n)}\) non si concentrano in alcune direzioni privilegiate, e la loro somma è “piccola.”