Siamo alla terza puntata della rubrica “Uno sguardo oltre la superficie“, a cura di Giuseppe Tinaglia. Uno spazio dove si osserva la geometria che ci circonda, ma anche oltre.

Nel primo articolo di questa rubrica, avevo parlato di una quantità geometrica chiamata curvatura di Gauss, per gli amici curvatura. In questo articolo voglio essere molto più ambizioso e parlare della curvatura dell’universo. Comincio quindi con il consigliare ai miei 24 lettori di rileggersi quell’articolo. In esso parlavo di come la curvatura sia una proprietà geometrica intrinseca di una superficie, nel senso che può essere calcolata da un essere vivente che vive nella superficie e a cui non è permesso lasciare la superficie. Esattamente come noi che viviamo nell’universo e non siamo in grado di uscirne, almeno per ora. In quell’articolo parlavo, ad esempio, di come la curvatura di un foglio sia zero e zero sia anche la curvatura di tutte le superfici che si possono creare utilizzando un foglio (ma senza accartocciarlo): un cilindro, un cono… Mentre, siccome la curvatura di una sfera è diversa da zero, la sfera e un foglio non solo appaiono diversi, come un cono e un cilindro, ma sono intrinsecamente diversi. Cioè è possibile distinguere tra le due superfici anche senza poterle abbandonare. Insomma calcolare la curvatura di una superficie non è soltanto un virtuosismo matematico, perché grazie a questo calcolo, si possono scoprire proprietà geometriche della superficie. Per esempio, soltanto la sfera di raggio R ha curvatura costante uguale a $$\frac{1}{R^2}$$, mentre le superfici che hanno curvatura zero sono quelle che si ottengono piegando un foglio.

Fatta questa premessa, la curvatura è una quantità geometrica che esiste, scusatemi la auto-citazione, oltre la superficie. Anche in spazi tridimensionali, come ad esempio l’universo, si può calcolare la curvatura. Quindi, senza andare, per il momento, troppo nel dettaglio delle conseguenze geometriche determinate dal valore della curvatura, la domanda sorge in maniera naturale: qual è la curvatura dell’universo?

L’argomento è ambizioso e prima di poter rispondere adeguatamente a questa domanda, bisogna risolvere altri problemi. Primo tra tutti, come si fa a calcolare la curvatura? Ci sono molti modi equivalenti di farlo. Una maniera molto geometrica, che funziona sia per oggetti a due dimensioni, come le superfici, che per oggetti  a tre o più dimensioni, come l’universo o il multi-verso, è usare i triangoli. Per esempio, dire che la curvatura di un piano è zero è equivalente a dire che la somma degli angoli di ogni triangolo è 180 gradi. La curvatura è positiva se la somma è maggiore di 180, negativa se minore… Argh, dimenticavo, ho bisogno di fare un’altra digressione! Facile parlare di triangolo nel piano, ma cos’è un triangolo quando la superficie è una sfera? Per dare una risposta soddisfacente a questa domanda bisogna generalizzare il concetto di segmento. È evidente che una proprietà di un segmento nel piano è il fatto di essere dritto, ma questa proprietà evapora quando si considerano altre superfici. Quali sono le linee dritte sulla superficie di una sfera? E poi, considerate questo: dopo avere tracciato una linea dritta su un foglio, se pieghiamo il foglio per farlo diventare un cilindro, quella linea non è più dritta. Eppure è la stessa linea, sullo stesso foglio! Insomma, il concetto di dritto è un concetto piuttosto effimero in questo contesto. Un’altra proprietà più radicale è invece il fatto che un segmento che collega due punti, è il cammino più corto che li collega. Ottimo! Questo concetto è più facile da esportare. Infatti, continua ad essere vero anche dopo avere piegato il foglio in un cilindro. Così, sulla superficie di una sfera, dati due punti, posso consapevolmente chiamare segmento quella linea che  minimizza la loro  distanza. Questi segmenti fanno parte di una famiglia di linee un po’ più numerosa, chiamate geodetiche. Si dà il caso che le geodetiche della sfera siano archi di cerchi massimo. Così, usando questa nuova definizione di segmento, data una superficie, possiamo chiamare triangolo, la figura geometrica che si ottiene collegando tre punti con tre segmenti. Questa è una generalizzazione naturale perché, se la usiamo nel piano otteniamo, i segmenti e i triangoli tanto amati da Euclide, la cui somma degli angoli è 180 gradi. Nel caso della sfera, dove i segmenti sono archi di cerchi massimo, la somma degli angoli di un triangolo è maggiore di 180 gradi.

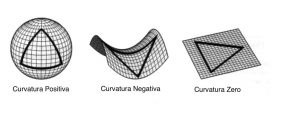E questo ci dice che la curvatura della sfera è positiva. Ci sono poi superfici che hanno curvatura negativa e… scusate, quasi dimenticavo che dobbiamo parlare dell’universo. Grazie a questa digressione abbiamo una idea di come calcolare la curvatura dell’universo. Ricapitoliamo. Un segmento è il cammino più corto che collega due punti. Un triangolo è la figura geometrica che si ottiene collegando tre punti con tre segmenti. La curvatura è zero, positiva o negativa se la somma degli angoli di un triangolo è uguale a, maggiore di o minore di 180 gradi. Problema, quali sono i triangoli nel nostro universo? Grazie ad Einstein sappiamo che  la presenza di massa influenza il calcolo delle distanze e, sempre grazie ad Einstein, sappiamo che i segmenti, nel senso, e lo ripeto per l’ultima volta, del cammino più corto che collega due punti, sono dati dalla traiettoria percorsa dalla luce. In altre parole la luce, che non è una sciupona, per andare da un punto a un altro sceglie sempre il percorso più breve. Voilà, finalmente sappiamo come creare segmenti, come creare triangoli e quindi come studiare la curvatura dell’universo. Uff!

Prima di continuare voglio fare una premessa. Le cose che ho discusso finora, le ho discusse in modo necessariamente vago per raggiungere tutti i miei 24 lettori. Le cose che discuto da questo momento in poi, invece, le discuto in modo necessariamente vago perché… beh le conosco solo in maniera superficiale. Innanzitutto, l’universo di oggi non è Euclideo, cioè non ha curvatura zero. Infatti, non ha curvatura nemmeno costante. Come dicevamo prima,  Einstein,  nella teoria della relatività generale, afferma che la presenza di massa influenza il calcolo delle distanze e quindi la costruzione di segmenti e triangoli. Quindi, le proprietà di un triangolo, come la somma dei suoi angoli, saranno diverse se questo triangolo si trova vicino a un buco nero o nello spazio intergalattico. Tuttavia si presume che, in passato (ma molto, molto, molto in passato), l’universo  fosse più omogeneo.  È in questo senso che si può parlare di curvatura dell’universo in maniera globale ed è questa curvatura che vogliamo calcolare.

Come sappiamo, noi non siamo al centro del nostro sistema solare, della galassia o dell’universo. Tuttavia non è egocentrico dire che siamo al centro dell’universo che riusciamo a vedere, così come siamo al centro del nostro orizzonte. Possiamo quindi immaginare l’universo visibile a noi come una palla di cui noi siamo il centro. È impensabile che non ci sia niente al di fuori di questa palla tuttavia, la luce di galassie fuori dalla palla non la vediamo perché non ci ha ancora raggiunto e quindi, in un senso che piace molto a certi fisici filosofi, quelle galassie per noi non esistono. Se siamo al centro di una palla, qual è il raggio di questa palla? Facile, il raggio di questa palla corrisponde all’età dell’universo… … … ehm ehm, ci sono domande? Forse che ho confuso unità di misura? Si e no. Siccome la velocità della luce è finita, noi possiamo vedere solo gli oggetti la cui luce ha avuto abbastanza tempo per raggiungerci. Quanto tempo ha avuto un raggio di luce per raggiungere la terra? Al massimo un tempo che è uguale all’età dell’universo, non un secondo di più, non uno di meno. Gli oggetti al di fuori di questa palla non li vediamo perché la luce da essi emessa non ha avuto abbastanza tempo per percorrere la distanza necessaria a raggiungerci. Ad essere precisi dunque, dovrei dire che il raggio di questa palla corrisponde alla distanza percorsa dalla luce in un tempo che è uguale all’età dell’universo. Tuttavia, siccome la velocità della luce è costante, parlare di lunghezza e di tempo è la stessa cosa. In realtà il calcolo dell’età dell’universo è parecchio complicato per via, tra le altre cose, dell’espansione dell’universo che non avviene a velocità costante.

Per semplificare la discussione che segue, chiamiamo età dell’universo, questa distanza, insomma questo raggio, T. Se prendiamo due punti sulla superficie di questa palla,  tali due punti sono equidistanti da noi e, utilizzando noi stessi come vertice, abbiamo costruito un triangolo isoscele con due lati di lunghezza T. Se fossimo in grado di trovare due punti sulla superficie di questa palla a distanza T tra loro, allora avremmo addirittura creato un triangolo equilatero. Qual è la misura dell’angolo di cui noi siamo il vertice e, saperlo, cosa ci dice sulla curvatura? Siccome stiamo studiando un triangolo equilatero, se fosse un angolo di 60 gradi, allora la curvatura dell’universo sarebbe zero, più di 60 gradi sarebbe positiva, meno di 60 gradi e sarebbe negativa. Purtroppo bisogna notare che, per via degli errori di misurazione, non si potrà mai sapere se questo angolo è esattamente un angolo di 60 gradi.

Chi è debole di cuore faccia attenzione. In quest’ultimo paragrafo la superficialità dei miei ragionamenti raggiungerà livelli criminali.

Preso un punto sulla superficie della palla, l’idea che ci permette di trovare un altro punto, a distanza T, sulla stessa superficie è la seguente. Sappiamo che la luce si muove ad una velocità costante, la velocità della luce appunto. Ma non solo, anche i campi gravitazionale ed elettromagnetico si muovono a velocità costante uguale alla velocità della luce. Per esempio, la luce del sole impiega circa otto minuti per raggiungerci. Quindi, se il sole sparisse in un istante, noi ce ne accorgeremmo solamente otto minuti dopo. Allo stesso modo, sentiremmo smettere l’influenza gravitazionale del sole solamente otto minuti dopo della sua vera scomparsa e non istantaneamente. Quanto tempo hanno avuto i punti sulla superficie della palla per “influenzarsi?” Come discusso prima, esattamente T. Esattamente come noi, un punto, chiamiamolo A, sulla superficie della “nostra” palla può essere pensato come il centro di una nuova palla di raggio T. I punti sulla superficie della “nostra” palla che sono anche dentro questa nuova palla di centro A hanno subito l’influenza gravitazionale ed elettromagnetica del suo centro A, mentre quelli fuori no. L’idea dunque è di fotografare la superficie della palla, notare queste differenze e così trovare due punti a distanza T per costruire il più grande e magnifico triangolo equilatero mai costruito. I fisici sanno come osservare le differenze tra l’ammasso di materia che ha avuto abbastanza tempo da subire l’influenza gravitazionale o elettromagnetica del punto A, e la parte di materia che non l’ha subita. Seguendo questi ragionamenti e dipendentemente dalle proprietà dei triangoli nel nostro universo, hanno creato tre modelli di come questa foto dovrebbe essere. Senza badare al significato dei colori, la prima figura rappresenta la foto assumendo che la curvatura sia positiva, la seconda zero e la terza negativa.

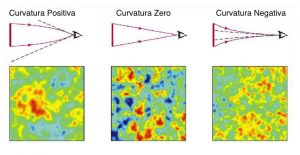
Nel 2000, la superficie della nostra palla è stata fotografata durante il cosiddetto BOOMERanG experiment  A Flat Universe from High-Resolution Maps of the Cosmic Microwave Background Radiation  e quello che si è fotografato, che non è proprio la luce ai confini dell’universo, ma la cosiddetta radiazione di fondo, è questo.

Stupendo! Solo io noto qualche somiglianza con il modello a curvatura zero? Spero di no. Ed è grazie a questo esperimento che sappiamo che la curvatura dell’universo se non zero, è vicinissima a zero! Applausi!

Giuseppe Tinaglia
King’s College London