Mostrare che ogni poligono può essere tassellato con pentagoni convessi.
La risposta... Non cliccate qui se non ci avete pensato! Poi è troppo tardi!
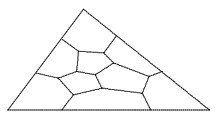
È noto che ogni poligono può essere tassellato con triangoli, quindi è sufficiente dimostrare che ogni triangolo può essere tassellato con pentagoni convessi. Dati due triangoli qualsiasi, uno può essere trasformato nell’altro per mezzo di una trasformazione affine (una trasformazione lineare seguita da una traslazione). Ma la trasformazione affine porta pentagoni convessi in pentagoni convessi. Quindi, è sufficiente dimostrare che almeno un triangolo è tassellabile con pentagoni convessi per dimostrare che lo sono tutti. Il caso particolare in figura risolve quindi il problema generale.
I Rudi Mathematici (Rodolfo Clerico / Rudy d’Alembert, Piero Fabbri / Piotr Rezierovic Silverbrahms, Francesca Ortenzio / Alice Riddle) sono autori della omonima e-zine di matematica ricreativa, pubblicata in rete dal 1999.
Mi correggo, o rivisto il filmato che ho postato e, verso la fine, viene detto:
”
la definitiva dimostrazione formale di altre possibili soluzioni è recentissima, parliamo del 2017.
“.
… che, questa volta, sia definitiva realmente?
Questo filmato fa un po’ la storia di Marjorie Rice:
https://www.google.com/search?client=ms-android-google&sca_esv=026fd76a3624c384&sxsrf=AHTn8zrpaImxG_TG0MyTSnDkXy7pFej5jA:1740115616518&q=Marjorie+Rice+rudi+mathematici+pentagoni&udm=7&fbs=ABzOT_CWdhQLP1FcmU5B0fn3xuWpA-dk4wpBWOGsoR7DG5zJBjLjqIC1CYKD9D-DQAQS3Z44LBK6yTXN_5587Z3ya9D7laQQbWKPISWgNRob6Daprkk-zUIxiKyt6kJGubBXcnSskv-nPl4YBtYSHE0jpocalybzvt9fU_bXu1mAPcgeUhr6eOG7ra4kdLSv5sEonKn9hNG4&sa=X&sqi=2&ved=2ahUKEwjrzMLpg9SLAxXj0wIHHXvAEIkQtKgLegQIEhAB&biw=432&bih=768&dpr=2.5#fpstate=ive&vld=cid:d6b10fa0,vid:nhTKP1syHf0,st:0
valter, “non ho capito a chi ti riferisci parlando di: “piano tassellato” “.
Non mi riferisco a nessuno, mi riferisco al fatto che la tassellatura (del piano) è un argomento vasto e complesso anche senza metterci dentro Escher e Penrose. Essendo un poligono qualunque una porzione del piano, è uscito quel “piano tassellato” che in effetti è un po’ troppo generico visto che il piano (infinito) è privo di bordi, mentre che un poligono qualsiasi i bordi li ha ed è colà che si gioca parte del problema, peraltro dato per risolto.
Imprecisione mia, chiedo venia: mai pensare che ciò che a volte diamo per sottinteso sia in tal modo da altrui percepito.
Quando dici piano tassellato dici [censura!!!!].
Tutto ruota, letteralmente, attorno all’angolo giro, che te lo devi coprire in tutti i punti, o vertici, del piano velleitario di presunta tassellabilità (se voi Rudi osate “pentagonati” io oso tassellabilità, tsk), e per questo il pentagono regolare col suo 108° che non divide 360° non tassella un tubo, o forse sì ma solo se il tubo è un toro 3d. Comunque e al di là delle facezie, ai non matematici nella loro profonda ignoranza (absit iniuria verbis io faccio parte dei non medagliati), piace dire che “la matematica non è un’opinione”, mentre che è vero il contrario: i pentagoni tassellanti sono 5, no 7, no 9, dài 10! (il punto esclamativo non è il fattoriale)… poi ti arriva la signora Marjorie Rice, casalinga, e i pentagons diventano 14 o giù di lì, e tuttora, a parte che sopra i 6 lati proprio non si può, siamo mica sicuri se abbiam detto l’ultima parola/pentagonata.
@yop
Riguardo a:
”
Quando dici piano tassellato dici [censura!!!!]
”
non ho capito a chi ti riferisci parlando di: “piano tassellato” (non mi sembra che qualcuno ne abbia accennato)?
Riguardo a:
”
… e i pentagons diventano 14 o giù di lì, e tuttora, a parte che sopra i 6 lati proprio non si può, siamo mica sicuri se abbiam detto l’ultima parola/pentagonata.
”
In effetti ne è stata trovata una 15.ma e quindi il (… o giù di lì) è giustificato.
Ho trovato questo link che me parla:
https://notte.dmf.unicatt.it/2017/img/postertassellazioni.pdf?utm_source=chatgpt.com
Il testo in questione è il seguente:
I primi 5 pentagoni furono scoperti dal matematico tedesco Reinhardt nel 1918, successivamente Kershner ne scoprì altri 3. Nel 1975 Martin Gardner divulgò nella sua rubrica su Scientific American queste scoperte e una casalinga di San Diego trovò così nuove tassellazioni. La lista salì a 13 e, nel 1985, a 14. Infine, nel 2015, Casey Mann, un professore di matematica dell’università di Washington e i suoi collaboratori scoprirono un ulteriore pentagono.
Ho letto anche, ma non trovo più dove, che non esiste ancora una dimostrazione formale che questi 15 siano tutti quelli possibili; … quindi pure il: “siamo mica sicuri …” vale ancora.
Ho letto il suggerimento dove si dice che ogni triangolo può essere tassellato da pentagoni convessi.
Ho fatto alcune prove e credo che ogni triangolo possa essere tassellato anche da pentagoni concavi (ed uno solo convesso).