Nel 1694, Isaac Newton e David Gregory, eminente matematico scozzese e Savilian professor di Astronomia all’Università di Oxford, ebbero una disputa matematica che sarebbe diventata storica. Il problema geometrico che affrontarono fu: qual è il numero massimo di sfere identiche che possono toccare contemporaneamente una sfera centrale dello stesso raggio nello spazio tridimensionale? Durante la discussione, Newton sostenne che il numero massimo fosse 12. Tuttavia, David Gregory ipotizzò che, con un’attenta sistemazione, potesse essere possibile farne toccare 13. La questione rimase senza soluzione per secoli. Entrambi gli scienziati non ebbero modo di sapere chi avesse ragione con certezza. Solo nel 1953 i matematici Schütte e van der Waerden fornirono la dimostrazione rigorosa che la congettura di Newton era corretta. Questa controversia tra i due matematici – che si stimavano a vicenda, Gregory aveva acquisito la sua posizione accademica anche grazie al sostegno di Newton – portò alla nascita del concetto del “kissing number”.
Il “kissing number” (o “numero di Newton”, o “numero di contatto”) di uno spazio, in geometria, è definito come il massimo numero di sfere unitarie non sovrapposte che possono essere disposte in quello spazio in modo che ciascuna tocchi una sfera unitaria comune. Per un dato impacchettamento di sfere (disposizione di sfere) in un dato spazio, il kissing number può anche essere definito per ogni singola sfera come il numero di sfere che tocca.
In due dimensioni, per intenderci, il kissing number è 6

mentre in 3 dimensioni diventa 12
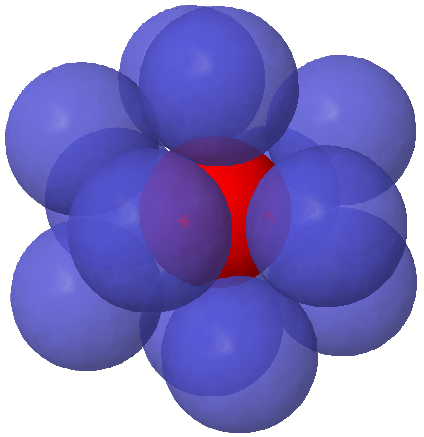
By The original uploader was Robertwb at English Wikipedia. – Transferred from en.wikipedia to Commons by Yelm., CC BY-SA 3.0
In 4 dimensioni, il kissing number diventa 24 (come dimostrato nel 2003 da Oleg Musin).
Quando le dimensioni aumentano, il problema diventa incredibilmente difficile. La risposta, attualmente, si conosce solo per le dimensioni 8 (240) e 24 (196.560). Non solo non si è andati oltre la dimensione 24, ma per quelle minori di 24 sono stati trovati solo degli intervalli in cui si pone il il kissing number. Per esempio, in dimensione 9, il kissing number è compreso tra 306 e 363. Per vent’anni, nessuno era riuscito a trovare qualche indicazioni per il kissing number in dimensioni sotto la 16, fino a quando AlphaEvolve, sviluppato dal laboratorio di AI di Google DeepMind, non è stato in grado di dimostrare che 593 fosse un limite inferiore in dimensione 11.
Ora, però, un nuovo studio pubblicato sulla rivista Linear Algebra and its Applications, ha fatto emergere nuovi limiti inferiori: precisamente, 510 nella dimensione 10, 592 nella dimensione 11 e 1932 nella dimensione 14. La ricerca, opera del dottorando Mikhail Ganzinhov dell’Università di Aalto in Finlandia, ha dunque presentato nuovi indizi in tre dimensioni minori di 16, e solo nel caso di quella 11 Ganzinhov è stato “battuto” da AlphaEvolve anche se “credo che il limite inferiore si possa spingere ben oltre 600” ha dichiarato il dottorando (in dimensione 11, il più piccolo limite superiore trovato finora è 868).
“Ho ridotto le dimensioni del problema cercando solo disposizioni con un alto grado di simmetria”, ha spiegato Ganzinhov e sugli sviluppi futuri, il suo relatore di tesi, Patric Östergård, è ottimista: “L’intelligenza artificiale può fare cose straordinarie, ma è tutt’altro che onnipotente, e il gioco potrebbe ancora volgere a favore di Mikhail anche nella dimensione 11”. In effetti, è un campo di ricerca in evoluzione. Il professor Henry Cohn del MIT e la ricercatrice Anqi Li pubblicheranno infatti nuovi risultati che estendono i limiti del kissing number nelle dimensioni da 17 a 21, il primo progresso in queste dimensioni in oltre 50 anni. Nonostante sembri (anche dal nome) un problema abbastanza bizzarro, il kissing number potrebbe avere importanti applicazioni pratiche in settori come le comunicazioni mobili e la navigazione satellitare.