Romain Dujardin,  Professore presso l’Université Pierre et Marie Curie di Parigi   ha pubblicato su  Images des Mathématiques, l’articolo «Comment partager un secret?».  Elena Toscano lo ha tradotto per noi.

Succede di incontrare numerose situazioni pratiche in cui può essere utile spezzettare un segreto in più parti:

• Un’azienda è di proprietà di 10 soci un po’ diffidenti. Ci tengono che 7 di loro siano d’accordo per ogni spesa. Come stabilire un protocollo per assicurare che un’alleanza tra 6 o meno azionisti non possa trasferire i conti?
• Il Presidente Trump dimentica ripetutamente il codice nucleare e pertanto deve annotarlo da qualche parte. Per garantire la massima sicurezza lo Stato Maggiore decide di spezzettarlo in diverse parti conservate in 12 bunker disseminati su tutto il territorio degli U.S.A in modo che, se il nemico prende 5 qualsiasi di questi bunker, il codice potrà essere comunque ricostituito senza finire nelle mani del nemico.
• L’azienda Cumulus Inc. specializzata nello stoccaggio online possiede una ventina di server sparsi sul pianeta. Assicura ai suoi clienti che il sistema funziona anche se la metà dei suoi server si trovano offline e che i dati rimangono riservati anche se molti di essi sono piratati.

Una soluzione rudimentale a questo problema è la seguente (ragioniamo nel caso della società per azioni, le altre situazioni sono simili):
si conserva il numero di conto in una scatola chiusa con diverse serrature e si distribuiscono a ciascun azionista un certo numero chiavi in modo che 6 azionisti non abbiano mai contemporaneamente tutte le chiavi. Un semplice ragionamento mostra che la soluzione richiede almeno 210 serrature sulla scatola e 84 chiavi per ogni azionista… Insomma sono troppe! E resta ancora da trovare un algoritmo per assegnare le singole chiavi…

Dettagli del ragionamento

Vi sono $$\binom{10}{6}=210$$  gruppi distinti di 6 persone, numerati da  $$G_1$$  a $$G_{210}$$. Per aprire la cassaforte al primo gruppo  $$G_1$$ manca una chiave $$s_1$$. Al gruppo  $$G_2$$ manca un’ulteriore chiave $$s_2$$: infatti se l’unica chiave mancante al gruppo $$G_2$$  fosse la $$s_1$$, si potrebbe trovare un sottoinsieme di 7 persone nell’unione $$G_1\cup G_2$$ che non possono aprire la scatola. Continuando a ragionare in questo modo si dimostra che al gruppo  $$G_i$$ manca un’ulteriore chiave   $$s_i$$ diversa da quelle precedenti. Con lo stesso ragionamento sarà possibile trovare un gruppo di 7 persone tra  $$G_i$$ e $$G_j$$, per qualche $$j<i$$ , non in grado di aprire la scatola. La conclusione di questo ragionamento è che sono necessarie almeno 210 serrature sulla scatola. Inoltre, ciascun azionista deve avere addosso almeno $$\binom{9}{6}=84$$ chiavi poiché ogni gruppo di 6 azionisti tra i 9 rimanenti deve avere la chiave mancante a quel gruppo.

Ecco un metodo elementare e molto efficace proposta da Adi Shamir [1] in un celebre articolo [2].

Per comprendere l’algoritmo iniziamo con una situazione molto semplice. La coppia più famosa dell’informatica, Alice e Bob, vorrebbe condividere il codice a 4 cifre della loro carta di credito, un numero segreto detto S compreso tra 0000 e 9999. Per fare questo basta scegliere due numeri interi a e b tali che $$a+b=S$$  e fornire a ad Alice e b a Bob. Se vogliono fare un acquisto insieme devono semplicemente sommare i loro rispettivi codici. [Ciò richiede di immaginare un dispositivo tecnico che permetta a ciascuno dei due di immettere segretamente il proprio codice, ma non è questo il punto qui]. Tutto ciò è molto semplice ma c’è una potenziale falla: supponiamo che Alice si veda assegnato il codice $$a=9958$$. In tal modo dispone di un’informazione fondamentale su S: è compreso tra 9958 e 9999 quindi può determinarlo in al più 42 tentativi. Non molto robusto come algoritmo… soprattutto se si tratta di un codice nucleare!

Per ovviare a ciò, un trucco classico è quello di lavorare modulo 10000, cioè fare il calcolo sommando o sottraendo tutti i multipli di 10000 necessari a ricondursi a un valore tra 0000 e 9999, ad esempio 8545+2651=11196=1196. Si può quindi scegliere a caso a compreso tra 0000 e 9999 e porre $$b=S-a$$. Si vede che ora la conoscenza di a non fornisce più alcuna informazione su S.

Ora, come fare per condividere un segreto con  persone in modo che per rivelarlo siano necessarie almeno 2 di esse? L’idea di Shamir è quella di considerare semplicemente…una retta.

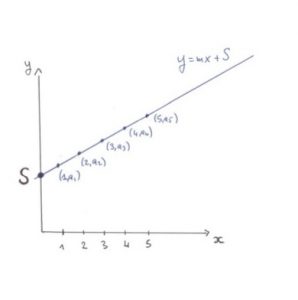In effetti una retta è completamente determinata da due dei suoi punti e, viceversa, la conoscenza di un punto sulla retta rivela poche informazioni su di essa. In formule, supponiamo che il nostro segreto sia un numero naturale S e scegliamo una retta nel piano passante per il punto $$(0,S)$$ la cui equazione è della forma $$y=mx+S$$ (con m numero intero). L’informazione fornita al partecipante  $$A_i$$ è il punto di ascissa i sulla retta, ossia il punto di coordinate $$(i,a_i)$$. Se due partecipanti inseriscono i propri codici  $$(i,a_i)$$ e $$(j,a_j)$$,  il computer calcola la pendenza $$m=\frac{a_j-a_i}{j-i}$$  e deduce S mediante la formula.  Forte, no?

In pratica c’è lo stesso errore di prima e, piuttosto che con numeri naturali, è preferibile lavorare modulo N con N numero intero sufficientemente grande. Meglio ancora è preferibile scegliere come valore di N un numero primo: di seguito alcuni dettagli.

Spiegazione

Si supponga che il codice di Alice sia (1,37). Delle due cose una: o il codice è compreso tra 0 e 37 o la pendenza della retta è negativa. Dato che per ipotesi tutti gli  $$a_i$$ sono numeri interi positivi, ci sarà per esempio $$a_2=2m+S$$. Ma $$37=m+S$$  quindi $$a_2=m+37$$ e quindi $$m\geq -37$$. In ogni caso si può concludere che  $$0\leq S\leq 74$$, che non è esattamente un numero ristretto di possibilità… Va bene, lavoriamo modulo 10000! Il problema è che il calcolo della pendenza fa intervenire una divisione e le divisioni modulo 10000 sono mal definite: $$\frac{5226}{2}=2613\equiv \frac{15226}{2}=7613$$, quale scegliere? Il fatto è che 10000 è divisibile per 2 e la soluzione è lavorare modulo p, dove p è un numero primo, ad esempio 10007 che è prossimo a 10000. La struttura matematica in cui si effettuano i calcoli viene chiamata campo finito  e in essa valgono le regole ordinarie dell’algebra [3].

Andiamo avanti! Se ci vogliono 3 persone per rivelare il segreto utilizziamo allora una parabola. La sua equazione sarà della forma $$y=m_2x^2+m_1x+S$$, dove S è il segreto. Si distribuiscono quindi ai partecipanti dei punti distinti  $$(i,a_i)$$, sulla parabola e, indipendentemente dal numero dei partecipanti, ci vogliono 3 punti per determinarla e così svelare il segreto S.

Tornando al problema originale, la nostra società per azioni deve scegliere a caso un polinomio P di grado 6 (in un campo finito abbastanza grande da contenere le informazioni relative al segreto)

$$P(x)=m_6x^6+m_5x^5+m_4x^4+m_3x^3+m_2x^2+m_1x+S$$

in cui il termine costante è il numero del conto bancario e distribuire ai suoi azionisti i valori  $$P(1),\dots,P(10).$$  Per svelare il segreto al momento voluto, rispetto alla soluzione di aprire 210 serrature su una scatola, il procedimento per invertire il metodo di Shamir è molto semplice e consiste nel determinare mediante un semplice calcolo l’unico polinomio di grado 6 che interpola 7 (o più) valori noti. Per far ciò esiste una formula esplicita, tanto temuta dagli studenti, conosciuta come la formula di interpolazione di Lagrange [4].

Formula di interpolazione di Lagrange

Siano dati $$n+1$$  scalari distinti $$x_i$$, $$1\leq i\leq n+1$$ e dei valori  $$y_i$$.  Si cerca un polinomio P di grado n (che sarà in realtà unico) tale che per ogni i, $$P(x_i)=y_i$$ . Innanzitutto si osserva che per ogni  $$j$$ il polinomio  $$P_j$$  definito dalla formula:

$$P_j(X)=\frac{(X-x_1)(X-x_2)\dots(X-x_{j-1})(X-x_{j+1})\dots(X-x_{n+1})}{(x_j-x_1)(X-x_2)\dots(x_j-x_{j-1})(x_j-x_{j+1})\dots(x_j-x_{n+1})}$$

(si noti che il j-esimo fattore viene omesso) verifica $$P_j(x_j)=1$$ e $$P_j(x_i)=0$$ per $$i\not=j$$. Pertanto basta porre: 

$$P(X)=\sum_{j=1}^{n+1}y_jP_j(X)$$

• [1] Adi Shamir, matematico e crittografo israeliano celebre per essere la «S» di RSA.
• [2] How to share a secret, Communications of the ACM, 22 (11) (1979) : 612–613. Due pagine e più di 11000 citazioni ad oggi, roba da far girare la testa allo scienziato medio…
• [3] Un computer preferirà sicuramente lavorare in un campo di $$ 2^{14}=16384$$ e persino $$ 2^{15}=32768$$ elementi.
• [4] Andate subito a vedere questo appassionante documentario  su uno scienziato fuori dal comune.