Un eccitante prequel della Matematica del colore, attraverso la storia degli scienziati che nel diciottesimo e diciannovesimo secolo hanno dato una struttura rigorosa alla sensazione del colore. Ci regalano questo viaggio, Edoardo Provenzi, Professore all’ Université de Bordeaux e Valentina Roberti, assegnista di ricerca presso l’Università di Padova. Questo è il secondo episodio. Tutti gli episodi usciti li trovate in questa pagina.

È ben noto che, fin dall’antichità, i pittori fecero di necessità virtù imparando ad utilizzare le poche sostanze colorate presenti nella loro zona di attività o disponibili ad un prezzo abbordabile (si pensi per esempio alla scarsità e al prezzo esorbitante dei lapislazzuli usati da Giotto), per riprodurre una grandissima quantità di sensazioni di colore nelle loro opere.

Per uno scienziato, questa sorta di magia è un irresistibile mistero da risolvere e, soprattutto, pone una domanda molto intrigante: qual è il minimo numero di pigmenti che possono essere utilizzati per generare anche le altre sensazioni di colore? L’esperienza maturata dai pittori portava ad una duplice convinzione: che esistessero colori primari e colori composti (o secondari) e che bastassero solo tre pigmenti primari per ottenere tutta la gamma dei colori secondari entro certi limiti di intensità e purezza.

È anche nel tentativo di formalizzare questa evidenza empirica che si svilupparono i modelli per la rappresentazione del colore, a partire dal Settecento. Non è un caso che una della figure che contribuì in modo più significativo a rispondere a questo interrogativo sia Hermann Günther Grassmann (1809-1877), l’inventore dell’algebra lineare, già citato nell’episodio 3 de “La matematica del colore”, disponibile qui.

Infatti, in matematica, la possibilità di “ricostruire” tutti gli oggetti di uno spazio a partire da un numero limitato di elementi corrisponde al concetto di base di uno spazio vettoriale, presentato per la prima volta proprio da Grassmann nel 1844.

La pratica dei pittori venne codificata in forme diverse dagli scienziati che proposero i loro modelli, chiamati “diagrammi del colore”, inizialmente facendo uso dalla triade dei colori primari dei pittori. I diagrammi proposti da Mayer e Lambert nel Settecento costituirono i modelli di riferimento in ambito scientifico. Vediamo più da vicino in cosa consistono.

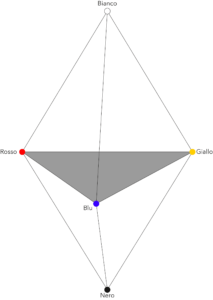
Tobias Mayer (1723-1762), astronomo, cartografo e matematico tedesco, elaborò per primo nel «De affinitate colorum commentatio», pubblicato postumo nel 1775, un modello tridimensionale per la rappresentazione del colore partendo dai tre primari dei pittori, giallo, rosso e blu, e posizionandoli ai vertici di un triangolo equilatero. Si noti che la scelta del triangolo equilatero è motivata da ragioni di coerenza: è, d’altronde, il poligono regolare con tre lati, come il numero dei primari!

L’intento di Mayer era quello di rappresentare tutti i colori distinguibili dal sistema visivo umano e, a tale scopo, escogitò quello che oggi chiamiamo comunemente un “solido del colore”, ovvero un diagramma cromatico tridimensionale per rappresentare i colori distinguibili partendo dai tre primari dei pittori, insieme al bianco e al nero. Per costruire il suo modello, che, utilizzando un linguaggio matematico rigoroso, corrisponde ad una bipiramide triangolare ottenuta unendo due tetraedri per una faccia, Mayer propose di assemblare una serie di triangoli di area via via decrescente verso i poli rappresentanti il bianco e il nero. Alla base pose il triangolo equilatero con giallo, blu e rosso ai vertici e fissò nel suo baricentro il grigio: in questo modo viene recuperato l’asse della luminosità di aristotelica memoria. Per Aristotele, infatti, il bianco e il nero sono colori, e, anzi, sono la matrice di tutti i colori, i quali risultano da una combinazione di bianco e nero in diverse proporzioni. Non è un caso che, a lungo, i colori siano stati pensati e classificati secondo un criterio acromatico, quello della chiarezza (o brillanza): seguendo un asse dal bianco al nero, il giallo era considerato come il colore più luminoso. Nella figura sotto possiamo vedere il solido del colore di Mayer.

 

L’obiettivo di Mayer era quello di stabilire quanti fossero i colori distinguibili dall’occhio umano. Avendo eseguito direttamente esperimenti con pigmenti, Mayer propose 12 colori per ogni combinazione di primari, introdusse altri 12 livelli di luminosità tra il triangolo di base e il vertice del bianco e altrettanti livelli tra la base e il vertice del nero. Il triangolo di base viene dunque ad assumere la forma rappresentata nella prossima figura, in cui ogni lato del triangolo è costituito da 13 elementi e  i numeri in apice rappresentano la quantità di pigmenti coinvolti in una data miscela. Le mescolanze di due colori primari sono situate sui lati del triangolo mentre le mescolanze di tutti e tre i colori primari si trovano al suo interno. La  somma di tutti i colori distinguibili nel triangolo di base è 91.

 

Aggiungendo il bianco e il nero alle varie mescolanze di pigmenti Mayer fu un in grado di ottenere triangoli di area via via decrescente, fino ad arrivare ai vertici. Sommando il numero di combinazioni nei vari triangoli, arrivò a stabilire il numero totale di colori distinguibili dal sistema visuale umano: 819.

È importante sottolineare che quello appena descritto è il primo modello tridimensionale del colore percepito. Circa 50 anni dopo, il pittore romantico Otto Runge (1777-1810) riprese indipendentemente la stessa idea, preferendo però alla bipiramide una sfera (il solido perfetto di Platone), modello ancora intriso di misticismo, che sarà di ispirazione per Goethe.

Malgrado il fatto che Mayer sia stato, storicamente, il primo ad introdurre una rappresentazione tridimensionale dei colori su base triangolare, il suo modello non ebbe l’ampia eco che avrebbe meritato. Dobbiamo a Lambert la sua riscoperta ed elaborazione.

Johann Heinrich Lambert (1728-1777), geniale matematico, fisico e filosofo, è noto ai matematici soprattutto per essere stato il primo a dimostrare nel 1761 un risultato fondamentale: l’irrazionalità di pi greco.

Lambert capì che nel modello di Mayer vi era una ridondanza che può essere eliminata: infatti, le rappresentazioni dei colori nel tetraedro inferiore e superiore sono identiche a meno della loro luminosità. Se assegniamo 1 alla luminosità del bianco e 0 a quella del nero, allora, un attimo di riflessione porta a capire che la luminosità dei colori appartenenti al tetraedro superiore è 1 meno la luminosità dei colori speculari appartenenti al tetraedro inferiore. Quindi, Lambert considerò inutile la doppia descrizione della luminosità e troncò la bipiramide lasciando una piramide semplice nel suo lavoro del 1772 intitolato “Beschreibung einer mit dem Calauschen Wachse ausgemalten Farbenpyramide”(“Descrizione di una piramide di colori dipinta con cera di Calau”).

Come mostrato dall’immagine sottostante, il triangolo alla base di Lambert contiene solamente 45 colori ed esistono sei livelli di luminosità crescente.

Il successo del modello di Lambert fu dovuto non solo alla semplificazione che egli apportò al modello di Mayer, ma anche al fatto che il pittore Benjamin Calau colorò il suo sistema di rappresentazione rendendolo di uso pratico per tintori e stampatori. Se i diagrammi del colore di Mayer e Lambert costituiranno i modelli di riferimento in ambito scientifico, quello sferico, introdotto da Runge nel suo lavoro “Die Farbenkugel” del 1810, rappresenterà uno dei modelli più significativi nell’ambiente dei pittori e sarà di ispirazione per Goethe.

                                                                                                                                                                                                                                                               #fine secondo episodio

Edoardo Provenzi e Valentina Roberti

curato da: Barbara Nelli