____________________0____________________
Chi è John M. Smith? Cosa ha di umido la Matematica? Che c’entra con l’Evoluzione? Perché
La Natura seleziona forme matematiche per ottenere vantaggio evolutivo?
Prima di andare al numero 1, leggi gli altri capitoli, qui.
____________________1____________________
1705, Basilea. La salma di Jakob Bernoulli viene consegnata all’antica cattedrale, Basler Munster, dove i suoi cari potranno offrire l’ultimo saluto. Sulla lapide un’iscrizione in latino

Jakob Bernoulli, matematico incomparabile
Professore all’Università di Basilea per più di 18 anni
Membro dell’Accademia Reale di Parigi e Berlino,
famoso per i suoi scritti…
Sotto, un cerchio con una spirale e la scritta

EADEM MUTATA RESURGO
Cambiata, eppure la stessa, risorgo
Bernoulli aveva studiato a fondo, riteneva la spirale simbolo di forza e costanza nelle avversità, del corpo umano che dopo la morte si ricrea nella sua esatta e perfetta essenza.
Quello che però non poteva immaginare è che nel momento esatto in cui lo scultore incise l’ultima lettera nella pietra, venne lanciata una maledizione, EADEM MUTATA RESURGO divenne una profezia; l’essenza della spirale cominciò a muoversi inquieta e a viaggiare nello spazio e nel tempo.
Vai all’85.
____________________2____________________
Da un trattato di falconeria.

“Il falco pellegrino (Falco peregrinus) è un uccello rapace della famiglia dei Falconidi.
La parola peregrinus fa riferimento alla colorazione scura delle penne del capo, che ricordano un cappuccio nero, come quello che solitamente indossano i pellegrini.
Come ogni altro rapace, caccia utilizzando becco e artigli per ghermire le prede, che consistono in altri uccelli, quasi mai animali terrestri.
Ha una lunghezza compresa tra 34 e 58 cm con un’apertura alare fra 80 e 120 cm; le femmine sono il 30% circa più grandi dei maschi.
Il falco pellegrino è l’animale più veloce del mondo, in grado di raggiungere e superare, in picchiata, i 320 Km/h.
È in grado di cacciare prede a mezz’aria.
Grazie al senso della vista molto sviluppato, la sua strategia di caccia consiste nel lanciarsi in picchiata da altezze considerevoli, raggiungendo grande velocità e seguendo una traiettoria a spirale sempre più stretta che culmina con la cattura della preda.”
Se pensi che quanto sai sia abbastanza, puoi proseguire andando al 12.
Altrimenti, gli indizi sono fra il 2 e l’11.
____________________3____________________
Da un’enciclopedia contenente argomenti di zoologia.
“Nautilus è un genere di molluschi cefalopodi ed è un esempio di fossile vivente; sebbene la sua conchiglia sia ben nota dal XVII secolo grazie ai commerci con le Indie orientali, fu osservato per la prima volta in vita solamente nel 1829.

Si presenta come una grossa conchiglia (anche oltre i 20 cm di diametro avvolta a spirale) con l’apertura rivolta verso l’alto in cui vive un corpo molle con una grossa testa composta da occhi grandi, un rugoso mantello posto a protezione di metà capo e carnosi tentacoli intorno ad un becco simile a quello di un pappagallo, con cui l’animale rompe le corazze dei crostacei di cui si nutre. I tentacoli sono molto numerosi, e organizzati in diversi ordini o anelli concentrici attorno alla bocca dell’animale; la gran parte di questi tentacoli è fissata alla base ad una sorta di “fodero” da cui il nautilus può estenderli o ritrarli a piacimento. A differenza di quelli di seppie, calamari e polpi, i tentacoli non hanno ventose, ma la loro superficie ruvida e irregolare permette comunque una presa salda.
All’interno della conchiglia sono presenti zone divise da pareti di madreperla, chiamate setti, che aumentano di numero con l’aumentare dell’età: sono le camere che il corpo dell’animale occupa a mano a mano che aumenta di dimensione; solo l’ultimo e più esterno dei setti è occupato costantemente dalle parti molli dell’organismo.”
Se pensi che quanto sai sia abbastanza, puoi proseguire andando al 12.
Altrimenti, gli indizi sono fra il 2 e l’11.
____________________4____________________
Questo indizio è particolarmente complicato, ancor più senza aver chiara la definizione di spirale archimedea. Forse non è il più utile per cominciare.
Immagina una corda attorcigliata, di diametro d.

La figura che forma è proprio una spirale archimedea della forma
$$ r=b\theta $$
Il coefficiente b si può ottenere a partire dal diametro tramite l’uguaglianza
$$ b=\dfrac{d}{2\pi} $$
e così si può calcolare la lunghezza della corda senza doverla svolgere.
La lunghezza di una spirale dal centro O ad un punto a $$ \theta $$ gradi è
$$ l=\int^{\theta}_{0}\sqrt{r^{2}\left( s\right)+r’^{2}\left( s\right)}ds $$
Ossia la formula esplicita, anche se non semplicissima
$$ l=\dfrac{b}{2}\left[ \theta \sqrt {1+\theta ^{2}}+\log \left( \theta+\sqrt {1+\theta ^{2}}\right) \right] $$
La quantità $$ \log \left( \theta+\sqrt {1+\theta ^{2}}\right) $$ è molto più piccola di $$ \theta \sqrt {1+\theta ^{2}} $$ quando l’angolo è grande e si può ignorare per un calcolo più rapido.
Ad esempio, una corda di un centimetro di diametro ($$ b=\dfrac {1}{2\pi} $$) che si avvolge 10 volte su se stessa ( $$ \theta=2\pi \cdot 10=20 \pi $$) è lunga approssimativamente
$$ l \simeq \dfrac {b}{2}\theta \sqrt {1+\theta ^{2}} = \dfrac {1}{4\pi } \cdot 20\pi \sqrt {1+400\pi } $$
3,15 metri circa.
Se pensi che quanto sai sia abbastanza, puoi proseguire andando al 12.
Altrimenti, gli indizi sono fra il 2 e l’11.
____________________5____________________
“I ragni sono un ordine di aracnidi comprendente circa 45000 specie e, assieme ad altri aracnidi come gli scorpioni, sono stati fra i primi animali a colonizzare le terre emerse.

Sono quindi artropodi (phylum degli invertebrati più noti, come millepiedi, granchi e insetti) terrestri, hanno il corpo suddiviso in due segmenti, cefalotorace e opistoma, e otto zampe.
Non potendo ingerire cibo solido a causa della ristrettezza dell’intestino sono costretti a secernere enzimi digestivi per liquefare gli alimenti, spesso insetti o ragni più piccoli. Sono infatti predatori che grazie alla loro capacità di produrre seta, nella maggior parte delle specie costruiscono le complicate strutture delle ragnatele, con lo scopo di catturare le prede volanti che hanno la sfortuna di restare invischiate. Esistono vari tipi di ragnatele (ad imbuto, aggrovigliata, …) ma ha colpito l’immaginario collettivo la tela dei generi Argiope, Cyclosa, Araneus, Nephila e Tetragnata, ovvero quella circolare.

Il primo ostacolo che il ragno incontra nella costruzione è il posizionamento del primo filo, orizzontale, su cui il resto della ragnatela risulterà sospesa; comincia secernendo un filo che farà pendere in basso, aspettando la prima corrente d’aria che trasporti la seta in alto facendola aderire al luogo adatto più vicino.
Fatto ciò, il ragno si muoverà velocemente dall’altra parte del primo filo rafforzandolo con un secondo, e ripeterà ciò finché avrà formato un’impalcatura sufficientemente resistente. Successivamente si porterà al centro del filo e si lascerà cadere continuando a secernere seta, costruendo così una struttura a Y; il punto in cui convergono i tre bracci sarà il centro della tela.
Tutti gli altri raggi verranno poi costruiti simmetricamente passando da uno dei tre settori della Y all’altro, assicurando resistenza meccanica.

Completata la struttura a raggi, il ragno si muoverà al centro della tela e inizierà a svolgere un nuovo filo, spostandosi verso la periferia, a spirale. Questo filo è provvisorio e verrà sostituito da una “seconda mano” di filo colloso, completando così il lavoro.”

Se pensi che quanto sai sia abbastanza, puoi proseguire andando al 12.
Altrimenti, gli indizi sono fra il 2 e l’11.
____________________6____________________
“Per quattrocento anni, un’infinità di uomini sono stati sviati dalle parole di Seldon L’altra faccia della Spirale. Per risolvere il problema si sono serviti della scienza fisica, misurando la distanza con il regolo il compasso. Come sai, la galassia non è semplicemente una figura ovoidale piana, e la Periferia non è nemmeno una curva chiusa. In effetti si tratta di una doppia spirale, con l’ottanta per cento dei pianeti abitati dislocati sull’Asse Principale. Terminus è al capo estremo di quest’asse, e noi ci troviamo al capo opposto, perché, qual è il capo opposto di una doppia spirale? Ovviamente il centro.”
Probabilmente questo indizio è inutile, anzi, sicuramente, pensa J.M.Smith.
Probabilmente ha ragione, anzi, sicuramente.
Se pensi che quanto sai sia abbastanza, puoi proseguire andando al 12.
Altrimenti, gli indizi sono fra il 2 e l’11.
____________________7____________________
Seppur non necessario, ti consiglio di leggere l’indizio 8 prima di questo.
Le spirali sono curve che si avvolgono attorno ad un determinato punto centrale e spesso sono usate nella simbologia di ogni tipo di cultura; ogni spirale sul piano è esprimibile in coordinate polari in maniera piuttosto semplice, con la distanza dei punti dal centro che dipende dall’angolo di rotazione.
Fra la grande varietà di forme, menzione speciale va alle spirali archimedee e a quelle logaritmiche.
Spirale archimedea

È stata una conquista già del III secolo avanti Cristo, quando Archimede di Siracusa la affiancò alle figure ottenibili con l’aiuto di squadra e compasso, protagoniste della geometria greca;
Grazie a tale aggiunta, il matematico riuscì a risolvere il problema della rettificazione della circonferenza con un’eleganza sorprendente.
Matematicamente, una spirale archimedea è esprimibile con
$$ r=a+b\theta $$
Il parametro a controlla il punto iniziale della spirale (con a=0 parte dal centro)

Nella prima a=0, nella seconda a=1
Variando il parametro b invece si può invertire il verso di rotazione (orario-antiorario) o allargare le spire.

Nella prima b=1, nella seconda b=-1, nella terza b=0,5
Spirale logaritmica

È una conquista più recente, essendo stata descritta nel dettaglio per la prima volta da Descartes nel XVII secolo e studiata poi da Jakob Bernoulli, alla quale si riferiva come “spira mirabilis”.
Matematicamente, una spirale logaritmica ha una scrittura simile a quella di Archimede
$$ \log r=a+b\theta $$
o, equivalentemente
$$ ab ^{\theta} $$
Le differenze fra le due curve sono notevoli, a cominciare dal fatto che le spirali logaritmiche non hanno un punto iniziale, ma si avvolgono all’infinito intorno al centro. Comunque il significato dei parametri è simile; al variare di a la spirale ruota, al variare di b si allunga o si stringe.

Diverse spirali logaritmiche al variare dei parametri
Se pensi che quanto sai sia abbastanza, puoi proseguire andando al 12.
Altrimenti, gli indizi sono fra il 2 e l’11.
____________________8____________________
Immaginiamo tu debba individuare un punto in un piano, ossia uno spazio a due dimensioni, ti saranno necessarie due “indicazioni”. Sia d’esempio la posizione di un oggetto su una mappa geografica, individuata tramite latitudine e longitudine. I due valori in generale sono detti “coordinate”.
Possiamo fissare due rette come “sistema di riferimento”; quali sono le coordinate del punto?

I valori di x e y sono detti coordinate cartesiane del punto P, la y indica l’”altezza” del punto, la x la posizione rispetto l’asse verticale di riferimento.
Non sono comunque le uniche coordinate che si possono assegnare. Potresti ad esempio dare la posizione del punto specificando la distanza di P dall’origine (o polo), indicandola con r, e l’angolo, $$ \theta $$, come in figura

Il raggio r può essere un numero positivo qualunque, così come l’angolo, che cresce in senso orario e fa un giro completo ogni 360° ( $$ 2\pi $$ in radianti). Anche queste coordinate polari individuano univocamente P.
Perché dovresti tener conto di due sistemi diversi, con quest’ultimo neanche troppo intuitivo?
Immagina una retta, questa
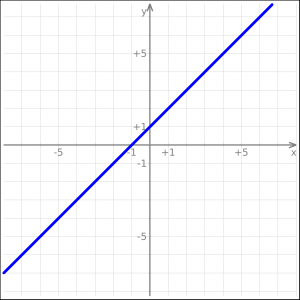
Grazie ai sistemi di coordinate è possibile descrivere forme geometriche in maniera compatta e maneggevole. In particolare, la retta sopra in coordinate cartesiane è
$$ y=x+1 $$
La stessa figura, in coordinate polari, diventa
$$ r= \dfrac {\sqrt {2}}{\sin {(\theta – \dfrac {\pi}{4}})} $$
La scrittura della retta è sicuramente più semplice nel primo caso, ma se prendiamo la circonferenza

abbiamo in coordinate cartesiane
$$ y=\pm\sqrt{1-x^{2}} $$
e, poiché ogni punto della figura ha la stessa distanza dal polo, la scrittura semplicissima in coordinate polari
$$ r=1 $$
Per alcune figure è più comodo un sistema cartesiano, per altre uno polare.
Se pensi che quanto sai sia abbastanza, puoi proseguire andando al 12.
Altrimenti, gli indizi sono fra il 2 e l’11.
____________________9____________________
Purtroppo la pagina è bagnata e l’indizio ormai è illeggibile. Speriamo non fosse importante!
Se pensi che quanto sai sia abbastanza, puoi proseguire andando al 12.
Altrimenti, gli indizi sono fra il 2 e l’11.
____________________10____________________
Il concetto di addizione fra due o più numeri è chiaro ai più, ma certo è meno noto che sia possibile sommarne anche una quantità infinita! Meglio, che è possibile sommare infiniti numeri e fare in modo che il risultato non sia infinito!
Se immagini di sommare la stessa quantità senza fermarti mai, ad esempio
$$ 1+1+1+1+\ldots $$
non ci sono speranze, il risultato sarà necessariamente infinitamente grande (e quindi non finito), ma puoi comunque pensare ad un esempio concreto con una somma infinita che dà un risultato finito.
Prendi un listello di legno, un righello di 20 cm di lunghezza;
dividendo in due parti uguali si ottengono due frammenti, entrambi di 10 cm.
Considera solo la seconda parte e dividila ancora in due metà uguali, di 5 cm l’una;
poi prendi la seconda di tali parti e dividila a metà…
continuando all’infinito con questo esperimento mentale.
Sommando, ossia mettendo insieme tutti i vari frammenti, si ottiene…
$$ 10+5+2,5+1,25+\ldots $$
…una somma infinita di termini sempre più piccoli che come risultato dà la lunghezza totale del righello, 20 cm.
In generale, indicando con
$$ a_{0},a_{1},a_{2},a_{3},a_{4},\ldots $$
i numeri da sommare, con il termine serie si denota la quantità
$$ a_{0}+a_{1}+a_{2}+a_{3}+a_{4}+\ldots $$
e si indica con il simbolo
$$ \sum_{n=0}^{\infty}a_{i}=a_{0}+a_{1}+a_{2}+a_{3}+a_{4}+\ldots $$
Una serie come quella del righello è detta serie geometrica e consiste nel sommare ripetutamente un numero positivo minore di 1 e tutte le sue potenze
$$ 1+\frac{1}{2}+\left(\frac{1}{2}\right)^{2}+\left(\frac{1}{2}\right)^{3}+\left(\frac{1}{2}\right)^{4}+\ldots $$
$$ \sum_{n=0}^{\infty}q^{n}=1+q+q^{2}+q^{3}+q^{4}+\ldots $$
La quantità q è detta ragione e si può dimostrare che tale somma ammette risultato finito, pari a
$$ \frac{1}{1-q} $$
che nel caso del righello, con q=1/2, dà proprio 2 (20 cm se consideriamo le unità di misura).
Sembra ragionevole immaginare che sia necessario sommare numeri sempre più piccoli per arrivare a quantità finite; questo è vero, ma è una condizione solo necessaria, ovvero esistono successioni di elementi sempre più miseri che però non sono “abbastanza piccoli” da risultare in una somma finita, come questa
$$ 1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\ldots $$
Tale quantità è detta serie armonica e aumentando i termini non fa altro che crescere, sempre più lentamente, inesorabilmente verso l’infinito.
$$ \sum_{n=1}^{\infty}\frac{1}{n}=+\infty $$
Se pensi che quanto sai sia abbastanza, puoi proseguire andando al 12.
Altrimenti, gli indizi sono fra il 2 e l’11.
____________________11____________________
Per comprendere al meglio questo paragrafo è consigliata la lettura dell’indizio 10, a meno che il concetto di somma infinita non sia già chiaro nella tua mente.
Una spirale poligonale è una figura formata da segmenti retti che si avvolgono all’infinito, come questa

Grazie a questi oggetti è possibile creare particolari illusioni ottiche; immagina di costruire le seguenti due spirali:
una spirale geometrica
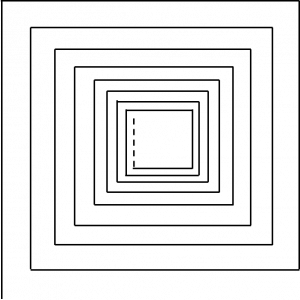
Le spire sono di lunghezza decrescente
$$ 1, \frac{9}{10}, \left(\frac{9}{10}\right)^{2}, \left(\frac{9}{10}\right)^{3}, \left(\frac{9}{10}\right)^{4}, \left(\frac{9}{10}\right)^{5}, \ldots $$
Una spirale armonica

Le spire sono di lunghezza decrescente
$$ 1,\frac{1}{2},\frac{1}{3},\frac{1}{4},\frac{1}{5},\ldots $$
Se provassi a calcolare la lunghezza totale sommando quelle delle varie spire, otterresti nel caso della prima
$$ 2 \left(1+ \frac{9}{10}+ \left(\frac{9}{10}\right)^{2}+ \left(\frac{9}{10}\right)^{3}+ \ldots\right)=2\sum_{n=0}^{\infty}\left(\frac{9}{10}\right)^{n} $$
e nel caso della seconda
$$ 2\left(1+ \frac{1}{2}+ \frac{1}{3}+\ldots\right)=2\sum_{n=1}^{\infty}\frac{1}{n} $$
Paradossalmente, la seconda sarà di lunghezza infinita, essendo una serie armonica, mentre la prima, apparentemente più fitta, dà luogo ad una serie geometrica di ragione
$$ q=\dfrac {9}{10} $$
e avrà lunghezza finita, pari a 20.
Se pensi che quanto sai sia abbastanza, puoi proseguire andando al 12.
Altrimenti, gli indizi sono fra il 2 e l’11.
____________________12____________________
Ora che hai raccolto abbastanza dati è il momento di passare al livello successivo:
Due indizi fanno una prova
A partire dal numero 13, e fino al 79, sono raccolte prove ottenute ragionando sugli indizi.
Una volta che ne avrai scelta una da leggere, sarà facile capire come è stata ottenuta, perché basterà scomporre il numero del suo paragrafo in fattori primi;
i valori risultanti sono i paragrafi degli indizi necessari a comprendere quella prova (ad esempio, se una prova fosse al numero 6, i corrispondenti indizi sarebbero 2 e 3, perché 2 per 3 fa 6).
Riuscirai a risolvere il mistero e capire perché la spirale continua a tormentare le vite di chi incontra? Scoprirai cosa le impedisce di quietarsi e riposare in pace?
Quando avrai radunato sufficienti prove, vai all’80.
____________________13____________________
L’acqua ha cancellato la prova, ormai è illeggibile.
Hai raccolto sufficienti prove? Vai all’80.
Altrimenti, puoi trovare le altre fra il 13 e il 79.
____________________14____________________
La figura che formano i falchi pellegrini in volo, nell’avvicinarsi ad una preda, è una spirale logaritmica e gode della proprietà di equiangolarità, mostrata da Torricelli per la prima volta.
Preso un punto P sulla spirale si traccino
- la retta che congiunge il centro e il punto P;
- la retta tangente la spirale in P.
L’angolo $$ \alpha $$ (in rosso nell’immagine) che le due rette formano fra loro rimane costante qualunque sia stata la scelta di P

I falchi hanno gli occhi posizionati lateralmente, in modo che formino un angolo $$ \alpha $$ con la direzione fronte-retro; il movimento a spirale logaritmica consente loro di avvicinarsi al centro, la preda, senza dover mai distogliere lo sguardo dall’obiettivo!
Allora sembra naturale che fra le spirali abbia scelto quella logaritmica. Certo, non è stato il falco a scegliere…
Hai raccolto sufficienti prove? Vai all’80.
Altrimenti, puoi trovare le altre fra il 13 e il 79.
____________________21____________________
La spirale del nautilus, o della chiocciola, è una spirale logaritmica e risponde a due esigenze di crescita dell’organismo, corrispondenti a loro volta a due proprietà matematiche:
Aumento della massa corporea.
Il nautilus esce dall’uovo già con la conchiglia e non se ne può separare. Crescendo costruisce strati superiori sul bordo della conchiglia che va ad occupare con la nuova massa corporea. La spirale logaritmica ha la proprietà di allargarsi man mano che si allontana dal centro e di conseguenza il volume aumenta. Una spirale archimedea ad esempio non consentirebbe un allargamento dell’area di uscita, ma solo un allungamento costante all’interno della conchiglia.

Nel dettaglio, la distanza tra due bracci di una spirale logarimica cresce come una successione geometrica; se la spirale è
$$ r = b^ {\theta} $$
la distanza fra due bracci consecutivi al giro $$ n $$ è
$$ \left( b^{2\pi}-1\right)\left( b ^{2\pi}\right)^{n} $$
Una curiosità; per quel che si è detto la distanza di ogni spira da quella successiva è in rapporto costante con la distanza dalla precedente. Se questo rapporto è uguale al numero aureo la spirale si dice aurea. La conchiglia del nautilus, seppur logaritmica, non è una spirale aurea, anche se tale erronea informazione si può a volte trovare in libri, o mostre.
Complessità strutturale
Come accade spesso in natura, gli organismi evolvono metodi semplici per ottenere risultati complessi. La forma a spirale logaritmica è una struttura complessa che però può essere generata tramite semplice sovrapposizione di moduli simili fra loro.
Si immagini un quadrato e lo si prenda come modulo fondamentale dal quale costruire la spirale. Lo si ingrandisca raddoppiando i lati e lo si ruoti di un angolo fissato (mettiamo 45°).
Procedendo allo stesso modo, ingrandendo e poi ruotando un numero arbitrario di volte si otterrà una figura che facilmente si può ricondurre ad una conchiglia di nautilus.

In effetti, si può mostrare che questa costruzione sta approssimando proprio una spirale logaritmica.
Allora sembra naturale che fra le spirali il nautilus abbia scelto quella logaritmica. Certo, non è stato il nautilus a scegliere…
Hai raccolto sufficienti prove? Vai all’80.
Altrimenti, puoi trovare le altre fra il 13 e il 79.
____________________35____________________
La tela circolare dei ragni ha la forma di una spirale di Archimede!

Un suggerimento del perché è dato dal suo nome alternativo, spirale uniforme.
Se prendiamo un punto qualsiasi sulla curva, poi percorriamo un giro completo e fissiamo un nuovo punto, a che distanza si troveranno i due?
Il primo sarà ad un angolo che chiamiamo $$ \theta $$, quello successivo ad un angolo più grande di 360°, o $$ 2\pi $$ radianti, quindi $$ \theta +2\pi $$.
I raggi corrispondenti saranno
$$ r_{1}=a+b\theta $$
$$ r_{2}=a+b\theta +2b\pi $$
Si può calcolare la distanza fra i due punti (distanza euclidea, non è complicato), ottenendo la quantità
$$ d=2\pi b $$
Quindi, poiché b è un numero fissato, la distanza fra i bracci, il passo, rimane costante per tutta la spirale, come si poteva immaginare già guardando i disegni.
Il ragno, con un solo filo, deve ricoprire la tela nella maniera più uniforme possibile (e meno dispendiosa dal punto di vista energetico dato che dovrà farla e disfarla ogni notte), evitare che ci siano buchi troppo grandi per non lasciare scampo alle prede.
Allora sembra naturale che fra le spirali abbia scelto quella archimedea. Certo, non è stato il ragno a scegliere…
Hai raccolto sufficienti prove? Vai all’80.
Altrimenti, puoi trovare le altre fra il 13 e il 79.
____________________77____________________
Dai disegni si può notare come la spirale archimedea abbia un punto iniziale, quello che si ottiene per $$ \theta =0 $$, quindi da ogni punto si può camminare all’indietro e raggiungere l’inizio dopo un opportuno numero di giri.
Discorso diverso per la spirale logaritmica, che si avvolge intorno al centro senza arrivarci mai; partendo da un punto P e muovendosi all’interno si deve girare infinite volte prima di raggiungerlo.
Tuttavia, la distanza coperta è finita. Come Bernoulli evidenziò nei suoi studi (la dimostrazione è precedente), se cercassimo di osservare nel dettaglio una spirale logaritmica, con una lente di ingrandimento sempre più forte, vedremmo riprodotta sempre la stessa identica curva, che si ripete uguale a se stessa ancora e ancora.
Autosimilarità è il nome di questa proprietà, caratteristica di molti sistemi naturali frattali…
Hai raccolto sufficienti prove? Vai all’80.
Altrimenti, puoi trovare le altre fra il 13 e il 79.
____________________79____________________
L’acqua ha cancellato la prova, ormai è illeggibile.
Hai raccolto sufficienti prove? Vai all’80.
Altrimenti, puoi trovare le altre fra il 13 e il 79.
____________________80____________________
La Natura seleziona forme matematiche per ottenere vantaggio evolutivo
Con il passare delle generazioni la spirale è stata selezionata come forma vincente in molti campi e, senza saperlo, animali matematici hanno portato in evidenza le sue proprietà, anche le meno banali…
Ma allora come si conclude il mistero? Come si collegano fra loro indizi, prove, natura e matematica? Perché la spirale continua ad essere turbata?
EADEM MUTATA RESURGO, una profezia che può essere anche interpretata secondo logica matematica: “Mi presento sempre uguale a me stessa, sono autosimile”.
Come insegnano falchi e nautilus e come Bernoulli aveva scritto e studiato per anni, solamente un tipo di spirale ha tale proprietà, ed è quella logaritmica!
Peccato che sulla tomba del matematico ci sia questo:
Una spirale archimedea! E la spirale archimedea ha molte proprietà utili, o non verrebbe scelta dai ragni, ma NON è autosimile!
Ebbene, uno scultore poco attento sbagliò il disegno, scambiando le spirali al momento della realizzazione della lapide e attirando le ire della spirale, che da quel momento esatto cominciò a viaggiare turbata…
Vai all’86.
____________________81____________________
In un libro d’arte si può trovare un’ulteriore traccia del percorso dell’inquieta spirale nel tempo.
“Intorno agli anni Settanta del Novecento l’attenzione di molti artisti si sposta dal particolare al generale, dal singolo oggetto allo spazio in cui tale oggetto è immerso. E poiché l’ambiente che ci circonda è generalmente quello naturale, la Land Art prende in considerazione spazi vastissimi, all’interno dei quali il segno artistico dell’uomo agisce con la stessa maestosa grandiosità di un evento atmosferico o di un cataclisma naturale. La Land Art agisce esclusivamente su elementi del territorio già esistenti, riducendo al minimo l’impiego di materiali estranei all’ambiente e al paesaggio. L’incisività di ogni operazione artistica di questo genere sta nel gesto con il quale l’uomo, utilizzando le forme della natura, modifica la natura stessa, anche se in modo effimero. L’artista land, infatti, interviene massicciamente, solcando deserti, allineando massi, deviando corsi d’acqua, creando dighe e barriere, ma con installazioni solitamente di brevissima durata.
Di primaria importanza il caso di Robert Smithson, statunitense, nato a Passaic il 2 gennaio del 1938. La sua più celebre e suggestiva opera è Spiral Jetty, realizzata nel 1970 sul Great Salt Lake, Utah, e oggi quasi del tutto cancellata dall’azione delle onde e del vento. Si tratta, come suggerisce il nome stesso, di una gigantesca banchina a forma di spirale, messa in opera con l’ausilio della tecnologia per il movimento della terra, dei cristalli di sale e dei massi di basalto necessari alla costruzione.

L’effetto che ne deriva, continuamente mutevole a seconda delle maree e delle condizioni di luce, allude a un gigantesco gorgo d’acqua spiraleggiante, ma può essere percepito solo parzialmente da un uomo nelle vicinanze, il che pone il non facile problema della fruibilità, da parte del pubblico, di realizzazioni di questo tipo. Del resto, come la natura non si preoccupa di rendere sempre visibili le sue meraviglie, anche gli artisti land antepongono al risultato finale delle loro creazioni l’atto del pensarle e la fatica, anche organizzativa, del realizzarle; riducendo l’espressione artistica al puro momento creativo, negano di fatto ogni valore agli oggetti prodotti, concentrandosi sull’idea…”
Vai all’83.
____________________82____________________
Apriamo una piccola parentesi per parlare di quello che sta succedendo già da qualche capitolo di “La Matematica Umida dell’Evoluzione”, parliamo di Retcon.
La retrocontinuity, continuità retroattiva, è un espediente narrativo a volte utilizzato in componimenti ad episodi (casi notevoli quelli della Marvel Comics), grazie al quale si modificano eventi e situazioni descritti in precedenza per adattarli ai nuovi sviluppi della storia; è esattamente quello che è stato usato per giustificare la presenza di “The Last Woman” nella biblioteca di J.M. Smith (o di Dodgson nella ciurma, in “Attraverso lo Specchio”). Le modifiche possono essere di varia natura e nel nostro caso si parla di retcon additiva, i nuovi dettagli della storia hanno colmato spazi vuoti con informazioni che sostengono punti attuali della trama e hanno mostrato che i personaggi hanno una “storia segreta”, che le loro vicende si svolgono indipendentemente dal fatto che ci sia qualcuno a raccontarle.
Chiudiamo la parentesi, che poi altro non è stata che una rottura della quarta parete, ulteriore espediente narrativo, e torniamo alla storia, all’84.
____________________83____________________
1859. John Maynard Smith sollevò lo sguardo dal libro che stava leggendo, accigliato: “Ma cosa…”
(Sì, si comporterà allo stesso modo anche un decennio più tardi, qui)
Affacciato dal suo brigantino guardava l’oceano, ormai compagno fisso da circa un mese, e rifletteva…
Tombe di matematici, astronomia inventata, forme d’arte degenerata,…non era più fantasia, ma follia!
Aveva comprato quel numero della rivista “The Last Woman” perché apprezzava l’autrice, l’inglese Mary Shelley e le sue composizioni visionarie che fondevano fantasia e scienza, come l’ormai celebre “Frankenstein” e il meno noto “L’ultimo uomo” che raccontava un mondo apocalittico invaso dalla peste (era proprietario di una copia della prima edizione del 1826 di quel libro tanto criticato).
Con quest’ultima serie di volumi del ’50, scritti un anno prima della sua morte, probabilmente si era spinta un po’ troppo oltre con l’innovazione ed era difficile da seguire.
Per affrontare la sua famosa lunga spedizione Smith aveva portato con sé molti testi delle più disparate materie, ricalcando le orme del suo inspiratore Charles Darwin, che della pluralità di stimoli aveva fatto tesoro, grazie a libri come i “Principi di Geologia” di C. Lyell sulla teoria dell’attualismo, dei cambiamenti geologici graduali e adirezionali, o testi del demografo T.R. Malthus sul problema della mancanza di risorse a causa la continua crescita delle popolazioni umane…
Comunque, nella biblioteca di Smith c’erano anche testi più leggeri, e “The Last Woman” era fra quelli. Presentato come collana di enigmi a sfondo scientifico, quel numero conteneva le tre storie di Bernoulli, Hubble e Smithson, poi proseguiva così:
“La spirale di Bernoulli continuò a reincarnarsi e a viaggiare inquieta da una generazione all’altra. Starà a te seguire gli indizi, ottenere le prove e capire cosa la turba, e perché”
Per una parentesi di tipo metaletterario, vai all’82.
Altrimenti la storia continua all’84.
____________________84____________________
Perché la spirale continua ad essere inquieta?
I paragrafi dal 2 all’11 contengono indizi utili a rispondere alla domanda; non è necessario leggerli in sequenza, né leggerli tutti (ma è consigliato).
Quando ne avrai a sufficienza potrai andare al 12.
____________________85____________________
30 dicembre 1924. Edwin Powell Hubble annuncia una scoperta grandiosa: la Via Lattea, la nostra galassia, non è l’unica galassia, ma una delle tante disperse nello spazio infinito.
Parte del merito è comunque anche da attribuire al lavoro di Henrietta Leavitt, che nel 1912 trovò il modo per misurare la distanza degli oggetti celesti, osservando le variazioni di luminosità di alcune stelle “pulsanti”, le Cefeidi.
Passando in rassegna il cielo stellato Hubble si concentrò su Andromeda, un corpo celeste sulla natura del quale gli astronomi discutevano da tempo…
A quale distanza si trova? È un ammasso di gas cosmico, una nebulosa?
Grazie alle leggi stabilite da Henrietta, ottenne un risultato: Andromeda è troppo lontana perché sia parte della nostra galassia e necessariamente è essa stessa una galassia, piena di stelle e pianeti! Improvvisamente, l’Universo divenne molto più grande.
Comunque Hubble dimostrò anche altro con la sua osservazione, una teoria che già nel 1845 l’astronomo irlandese Lord Rosse aveva rappresentato in uno schizzo, frutto di un’ossessione che per l’intera vita aveva tormentato entrambi gli scienziati

c’è una forma che si ripete invariata nello spazio e nel tempo, sulla Terra e nel cielo…anche alcune galassie sono a forma di spirale!
Vai all’81.
____________________86____________________
Basilea. Uno scultore solitario entra nell’antica cattedrale, Basler Munster. È notte, la chiesa è deserta e leggermente spettrale. Non si fa prendere da inutili ansie, è lì per compiere una missione, e sa che metterà fine una volta per tutte alla maledizione dell’EADEM MUTATA RESURGO.
Con grande sforzo solleva il blocco di pietra che ha trascinato vicino la lapide di Bernoulli e lo fissa alla parete. “Ecco, così va meglio”.

La spirale ritrovò la sua quiete.























