di Davide Palmigiani

____________________0____________________

____________________1____________________

Dopo aver prestato interesse ai rami vegetali dell’albero della vita (link), la nostra attenzione matematico-evolutiva si sposta verso uno dei rami più disprezzati, schifati, osteggiati, “pesticidizzati” del regno animale: la classe degli Insetti, e in particolare l’ordine degli Imenotteri, quel gruppo di animali che hanno “ali membranose” (quando le hanno), sei zampe, antenne, nessuna vertebra e un esoscheletro piuttosto morbido. Di chi stiamo parlando? Vai al 2.

Sì, l’articolo è pensato come un librogame, in poche parole un ipertesto vintage. Se comunque proprio non amate fare su e giù fra una sezione e l’altra e amate l’ ”effetto Wikipedia” ci sono dei link ad ogni scelta.

____________________2____________________

La Natura seleziona forme matematiche per ottenere vantaggio evolutivo (link) vuol dire che Evoluzione e Matematica si parlano, e si parlano anche a voce alta nell’ordine dei perlopiù disprezzati imenotteri, dove si possono trovare specie fedeli a svariate branche matematiche.

Se tu fossi un imenottero, a quale fazione apparterresti?

Fedele alla Geometria euclidea? Vai al 3.

Fedele alla Teoria delle Probabilità? Vai al 7.

Fedele ai Numeri Primi? Vai all’11.

Fedele all’Ottimizzazione? Vai al 12.

____________________3____________________

Sei un’APE, uno degli insetti sociali più conosciuti e, se non lo sapessi, hai un ruolo ecologico fondamentale, passando le giornate ad impollinare fiori. Sei un’esperta della geometria euclidea ma sicuramente non la conosci con questo nome; non la conosci con nessun nome in effetti.

La geometria euclidea è quella che si studia dalle medie, che parla di rette, piani, figure con lati e angoli, vecchia 2300 anni. Eppure da molto prima le api costruiscono favi che contengono esagoni regolari bene incastrati fra loro, costruzioni di eccezionale semplicità e bellezza. I favi sono fatti di cera secreta da ghiandole apposite delle api operaie e fungono sia da dispensa di miele e polline che da casa e culla di larve della covata, ma perché ha quella forma? Per comprenderlo c’è bisogno di immagazzinare due nozioni matematiche, proprietà dei poligoni regolari (vai al 4) e definizione di tassellatura (vai al 5).

Quando sarai pronto, potrai passare al 6.

____________________4____________________

Un poligono è una figura delimitata da una spezzata chiusa che non si intreccia, qualcosa del genere:

Un poligono regolare ha lati congruenti (ossia sovrapponibili) e angoli uguali.

È noto che siano infiniti, uno per ogni numero di lati, dal tre in su: triangolo equilatero, quadrato, pentagono, esagono, ettagono, ottagono, ennagono, decagono, endecagono, dodecagono, …

Questa caratteristica non è un’ovvietà, infatti se saliamo di dimensione e consideriamo l’equivalente nello spazio (dobbiamo richiedere anche che le facce siano uguali) otteniamo i poliedri regolari, detti solidi platonici, che sono solo cinque.

Fra la miriade di proprietà dei poligoni regolari ce ne interessano principalmente due:

– In ogni poligono (regolare e non) la somma degli angoli interni è sempre 180° moltiplicato per il numero di lati meno 2, quindi un parallelogramma ha somma pari a 180° per (4-2) = 360°, un pentagono 540°…

– L’area di un poligono regolare si può calcolare con facilità. Se connettiamo il centro della figura con ogni vertice otteniamo un numero di triangoli congruenti pari al numero di lati, quindi per ottenere l’area totale basterà moltiplicare l’area di un singolo triangolo per il numero di lati. L’area del triangolo si ottiene facilmente, base per altezza, dove la base è il lato e l’altezza prende il nome di apotema, un numero che si può calcolare e cambia da un poligono all’altro.

Concludiamo rispondendo ad una domanda che preannuncia la soluzione del problema delle api:

Se decido la lunghezza del perimetro, quale è il poligono regolare con l’area maggiore? O allo stesso modo, se avessi una rete di lunghezza fissata e dovessi delimitare il campo di forma poligonale più grande possibile, come dovrei mettere la rete?

Ad esempio, con un perimetro di 20, un quadrato ha area 25 (ogni lato misura 5), mentre un pentagono (di lato 4) ha area 27,5276…

La risposta non è complicata, perché non c’è! L’area, a perimetro fissato, è direttamente proporzionale all’apotema: se l’apotema cresce, l’area sarà maggiore. Ecco, l’apotema cresce con il numero di lati, quindi più sono i lati, più sarà grande l’area. Quindi il poligono con l’area più grande è quello con “infiniti” lati, quindi non esiste.

In realtà, se andiamo a disegnare in sequenza i poligoni regolari…

…diventano tondeggianti, come se il poligono con “infiniti” lati sia in realtà il cerchio (è proprio lui ad avere l’area maggiore, ma non è un argomento che ci interessa al momento).

Vai al 5 se vuoi avere qualche nozione sulle tassellature, altrimenti vai al 6.

____________________5____________________

Una tassellatura è un modo di ricoprire il piano con una o più figure geometriche ripetute all’infinito, una maniera matematica di dire “piastrellare il bagno”.

Qualche regola per una buona pavimentazione:

– i tasselli devono essere senza buchi e connessi (ossia un pezzo unico): Escher era un maestro di tassellature “esotiche” (guarda 0) ma noi ci interesseremo a pavimentazioni con tasselli poligonali regolari, quindi questa regola è rispettata.

– condizione di non scorrimento: ogni lato di un poligono deve combaciare con uno e un solo lato di un altro poligono, non come nella prima figura sotto

– condizione dei vertici identici: ogni vertice della tassellatura (i punti di incontro di tre o più figure) deve essere sovrapponibile ad ogni altro, potendolo ruotare e spostare, ossia deve essere uguale a ogni altro, se guardato dal giusto angolo, non come nella seconda figura sopra.

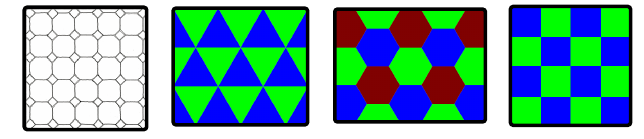
Queste sono tassellature ben fatte e ne esistono moltissime altre:

Se volessimo pavimentare sempre con lo stesso poligono però, non avremmo molto da poter decidere; se provassimo ad utilizzare ad esempio un ottagono non ci riusciremmo, ottenendo sempre delle poco estetiche fessure non ottagonali.

Esistono infatti solo tre pavimentazioni piane con poligoni regolari, perché la misura degli angoli del tassello deve essere un divisore intero di 360° per non avere buchi e quindi andranno bene solo il triangolo equilatero di 60°, il quadrato di 90° e l’esagono di 120°.

Vai al 4 se vuoi avere qualche nozione sui poligoni regolari, altrimenti vai al 6.

____________________6____________________

Siamo pronti a comprendere la motivazione del comportamento delle api, a patto di aver chiaro in mente che la Natura cerca sempre di ottimizzare in ogni modo, sforzandosi il minimo per ottenere grandi risultati.

Qual è il problema? Creare un favo di cera, con celle pronte a far da casa alle nuove nate.

In cosa si può risparmiare? Si può utilizzare meno cera possibile tramite una tassellatura che minimizzi le zone inutilizzate.

In cosa altro si può risparmiare? La forma delle celle sarà sempre la stessa, perché non ci sono particolari controindicazioni e, anzi, non si sovraccarica di informazioni il piccolo cervello di un’ape.

Queste risposte ci conducono alla probabile soluzione (probabile, perché nessuno ha mai assistito all’evoluzione dell’insetto): le api si sono evolute per creare celle grandi e spaziose utilizzando la minor quantità di cera possibile. Matematicamente è come cercare un poligono regolare che abbia l’area maggiore a parità di perimetro; in più deve essere un poligono che può formare una tassellatura. La scelta è univoca: solo triangoli, quadrati ed esagoni possono generare una tassellatura e poiché a parità di perimetro è la figura con più lati ad avere area maggiore…che esagono sia!

Vai al 13.

____________________7____________________

Sei una VESPA SOLITARIA, una sfecide, nera e affusolata, che si nutre di nettare e depone uova che daranno vita a larve carnivore.

Improvvisamente, il tempo comincia a scorrere velocemente all’indietro e ti ritrovi ad essere uno dei tuoi progenitori ancestrali di fronte ad una delle scelte più impegnative della storia degli imenotteri: Perché non cominci a collaborare con i tuoi simili, crei una colonia e diventi una formica? Vuoi rimanere sui tuoi passi e ritornare al tuo futuro di vespa solitaria?

Più di 80 milioni di anni fa una specie di imenottero simile ad una vespa cominciò a sviluppare comportamenti sociali e pian piano si specializzò dando vita alla grande famiglia delle formiche; alcuni momenti di questo passaggio sono impressi nell’ambra, nella quale si può osservare un esemplare di formica ancestrale, una sphecomyrna, che ha molte delle caratteristiche fisiologiche di una vespa. La motivazione può essere ricercata grazie alla matematica evolutiva, agli azzardi della teoria della probabilità.

Se credi ciecamente nella probabilità e vuoi arruolarti immediatamente nei ranghi della colonia, complimenti, sei diventata una formica, vai al 13, oppure al 12 se vuoi conoscere meglio i tuoi simili.

Se invece vuoi avere delle spiegazioni prima di decidere, vai all’8.

____________________8____________________

Apriamo una piccola parentesi: l’approccio che stiamo seguendo qui è differente da quello usato finora. Qui, invece di ragionare in questo modo:

Vedo una forma matematica in Natura, poi mi chiedo il perché evolutivo di quella forma

ragioneremo così:

Perché si è evoluto questo comportamento in Natura? Studiando trovo una spiegazione matematica

Chiudiamo la parentesi.

Il perché sta nel modello comportamentale degli insetti, nell’egoismo dei geni e nella struttura probabilistica della trasmissione dei caratteri genetici negli imenotteri.

Gli insetti hanno un modello di comportamentale filogenetico (opposto ad un modello ontogenetico, come il nostro e quello di specie più complesse), un modo per dire che, poiché la loro vita è relativamente breve, con poco tempo di apprendere dal mondo che li circonda tramite esperienza, avranno comportamenti piuttosto fissi, come “macchinette a molla”, faranno fondamentalmente solo quello che detta il loro codice genetico:

se sei un vivente, punti a trasmettere il maggior numero dei tuoi geni;

se sei un uomo, in più conosci l’affetto, la cultura, l’esperienza;

se sei un insetto, quello diventa il tuo scopo, il tuo fine, fare in modo che, nel futuro, i tuoi geni siano presenti nella maggior quantità possibile, massimizzando la possibilità di trasmetterli e vederli moltiplicarsi.

Nei mammiferi (non solo) il maschio e la femmina sono diploidi, hanno entrambi cioè coppie di cromosomi, presentano due copie della stessa informazione genetica, in versioni differenti (gli alleli di cui parla Mendel). Quando vengono generate le cellule sessuali, solo metà di questa informazione finisce nella cellula, così che, alla loro unione, si ricrea una cellula diploide, detta zigote, dalla quale si comincia a sviluppare l’embrione.

Durante la meiosi, il processo di formazione delle cellule sessuali, avviene il crossing over: i cromosomi che contengono la stessa informazione si scambiano dei pezzi generando variabilità.

Ciò che più ci interessa è notare che la metà del patrimonio genetico della madre passa ai figli ma, grazie al crossing over non è sempre la stessa metà (infatti i fratelli non sono identici fra loro); è una quantità aleatoria, casuale, che cambia per ogni figlio o figlia; ma, in media, quanta informazione genetica hanno in comune due fratelli?

Anche qui la risposta è la metà, grazie alla diploidia di entrambi i genitori e alla teoria della probabilità che, se non vi spaventano formule e parole strane, vi consiglia di andare al 9 per una spiegazione precisa.

Ben diverso e curioso è il caso degli imenotteri! Le femmine sono apparentemente normali, diploidi, mentre i maschi hanno solo metà del corredo cromosomico (nascono da uova non fecondate). Questa situazione porta ad un equilibrio differente: la madre donerà ad ogni sua figlia metà dei suoi geni, dopo una meiosi con tanto di crossing over, mentre il padre donerà tutto il suo patrimonio genetico alle figlie; così le figlie avranno in comune metà del patrimonio con la madre e con le eventuali figlie ma, in media, i tre quarti in comune con le sorelle, molto più di ogni mammifero (sempre al 9 c’è la spiegazione precisa di questo fatto). Allora, ragionandoci, per diffondere i propri geni, piuttosto che allevare figlie, conviene allevare sorelle, smettere di generare e dedicare la vita ad allevare la propria madre, così che possa produrre grande quantità di figlie femmine.

E i maschi? I maschi non hanno un padre e quindi hanno in media solo ¼ dei geni in comune con le sorelle, quindi perché accudirle? Meglio vivere alle spalle della colonia e specializzarsi in tutto ciò che riguarda l’inseminazione delle femmine.

Ecco, questo è esattamente il modello di funzionamento di una colonia, con la regina, unica femmina fertile, migliaia di sorelle operaie sterili e qualche fuco utile solamente come macchina di riproduzione.

Gli imenotteri sono spinti geneticamente a vivere in colonie, a basarsi sugli azzardi della probabilità! Convinta?

Sì? Bene! Benvenuta della famiglia delle formiche, vai al 12 o al 13 se hai fretta.

No? Hai avuto le tue spiegazioni e hai deciso in maniera cosciente, vai al 10.

____________________9____________________

Guarda qui, poi torna all’8.

____________________10____________________

Nulla da criticare, le spinte evolutive sono disparate e non esiste un meglio o un peggio in assoluto. Sei stata spinta verso il futuro delle vespe solitarie e sei perfettamente adattata al tuo ambiente. Sei una cacciatrice formidabile, capace di predare anche cavallette, che poi faranno da prima colazione per le tue larve, nate da uova che avrai avuto la cura di deporre nelle vicinanze.

Vai al 13.

____________________11____________________

Sei una CICALA del Tennessee, un insetto di uno degli ordini più diffusi e studiati al mondo e, sì, ti comporti come se conoscessi i numeri primi, MA…

non sei un imenottero, ma un Rincote, quindi mi dispiace, ma devi tornare al 2.

____________________12____________________

Sei una FORMICA, un esempio così evidente di insetto eusociale che è molto più sensato riferirsi a te come un neurone piuttosto che un animale, una piccola parte del super organismo che è il tuo formicaio; il vero “animale” è proprio lui, il formicaio, un sistema con comportamenti complessi formato da molte entità semplici come te. Nella tua semplicità riesci a risolvere problemi di ottimizzazione matematica di notevole interesse e l’aspetto più sorprendente è che non c’è neanche bisogno che tu capisca quello che stai facendo!

Ottimizzazione è una parola molto cara ai matematici, in special modo ai matematici numerici; risolviamo problemi di ottimizzazione ogni giorno, cercando il miglior ristorante in accordo al nostro budget, il miglior investimento di denaro, cercando la strada più corta per tornare a casa…

proprio in quest’ultimo problema le formiche sono maestre, sanno trovare le strade più corte.

Le formiche non progettano, non studiano matematica, vivono immerse nel loro mondo di odori, allora come fanno a calcolare il tragitto più breve dal loro formicaio ad una fonte di cibo? Che poi non sanno neanche dove sia la fonte di cibo inizialmente.

Le formiche sanno mettere in piedi un algoritmo probabilistico di ottimizzazione, o meglio, il formicaio sa risolvere questo problema complesso, perché una singola formica è stupida, è l’intelligenza collettiva ciò che conta.

Supponiamo di avere la seguente situazione, realizzabile sperimentalmente

Il formicaio è connesso al cibo solamente da due strade, una più lunga, l’altra ottimale.

Le formiche foraggiatrici cominciano ad uscire e muoversi casualmente fuori dal nido in cerca di cibo. Con il passare del tempo, qualche formica arriverà al cibo da una strada, qualcuna dall’altra e, dopo aver preso un po’ di cibo per la colonia, si dirigeranno nuovamente verso il formicaio, probabilmente guidate dal Sole, seguendo una strada non necessariamente ottimale, ma emettendo un feromone particolare, un segnale odoroso capace di attrarre le altre formiche; queste cominceranno allora a seguire la strada fino al cibo e, una volta giunte, raccoglieranno cibo e torneranno indietro emettendo feromoni.

Qui entra in gioco la componente del gioco più importante: la volatilità del feromone. Dopo un certo tempo l’odore svanisce e le formiche ne sono attratte sempre meno; se non evaporasse, ogni strada che conduce al cibo sarebbe trafficata allo stesso modo perché avrebbe sempre la stessa intensità di odore. Se invece la sostanza scompare, le strade più trafficate saranno quelle più odorose, perché più formiche lasceranno feromoni, e quindi sarà più odorosa e attirerà più formiche, che lasceranno feromoni, e quindi sarà più odorosa e… finché la maggior parte delle foraggiatrici camminerà sulla stessa strada.

Ma strada più trafficata non significa strada più corta, o sì?

Se è più trafficata, a parità di formiche vorrà dire che le stesse ci sono passate più spesso e quindi che, sì, la strada è più corta!

L’evoluzione ha favorito un comportamento coloniale, nel quale i singoli componenti hanno necessità di conoscere solamente il minimo necessario, il giusto che serva per compiere dei compiti elementari quali camminare, emettere feromoni e seguire strisce odorose. È interessante notare che non c’è neanche necessità che la singola formica sappia di essere parte di una colonia per far funzionare il meccanismo…

Il comportamento di cui abbiamo parlato può essere simulato al computer quasi alla perfezione se teniamo conto della semplicità e dell’essenzialità alla base del tutto, ed infatti esiste il programma Myrmedrome, scaricabile gratuitamente dal web, che simula feromoni, ricerca del cibo e movimenti casuali delle formiche; consigliato!

Vai al 13.

____________________13____________________

Qualunque sia stato il vostro percorso, i venti dell’evoluzione vi hanno spinto verso soluzioni funzionali e vantaggiose, ma ricordate che è la pressione selettiva dell’ambiente a soffiare e non un deus ex machina che risolve i problemi ragionando a tavolino, come noi; ma è questo il bello dell’Evoluzione, che si sa auto-organizzare…

…e l’auto-organizzazione è una proprietà dei sistemi complessi che, guarda caso, sono pura matematica.

____________________Bibliografia____________________

Formiche: storia di un’esplorazione scientifica – Bert Holldobler e Edward O.Wilson

Godel, Escher, Bach: un’eterna ghirlanda brillante – Douglas R.Hofstader

Imagine Math 2: between culture and Mathematics – a cura di Michele Emmer

Myrmedrome è un programma di Simone Cacace e Emiliano Cristiani

Roberto Natalini

Roberto Natalini [coordinatore del sito] Matematico applicato. Dirigo l’Istituto per le Applicazioni del Calcolo del Cnr e faccio comunicazione con MaddMaths!, Archimede e Comics&Science.