Uno spinoff de “La Matematica Umida dell’Evoluzione”

THE LAST WOMAN

di Mary Shelley

VOL. III

Immagino abbiate letto gli altri volumi di The Last Woman, proposti in precedenza (abbiamo pubblicato il volume I, il volume II, e parte del volume IV nella storia riguardante J.M. Smith). Quello che andiamo qui a presentare è il numero che completa la preziosa collezione.
Questo libretto è particolarmente significativo nel panorama della “letteratura nascosta” (i testi ritrovati solo recentemente) di fine ‘800, perché, oltre a presentare tematiche incredibilmente moderne in ambito di biologia evoluzionistica, qui si ha la prova incontrovertibile che Mary Shelley fu la prima vera scrittrice di fantascienza inglese, prima ancora del celebre “La Guerra dei Mondi” di G.H. Wells, di cui qui sotto riportiamo la copertina di un’edizione francese del 1906.
Sono quindi onorato di potervi presentare il terzo volume di The Last Woman e vi invito ad andare al numero 1.
Il curatore e traduttore della collana,

T.G. Dobzhansky

____________________1____________________

Al lettore.

Bentornato,
in questo terzo numero vorrei parlarti di quello che per me è un sogno a occhi aperti: l’idea degli altri Mondi.
Che sia la Luna, o che sia Marte, o ancora più lontano, chissà che non ci sia un posto in cui possano vivere altri uomini? Potremmo mai arrivarci? Saremmo noi, gli uomini, fra tutti gli organismi viventi, i più adatti alla vita su altri pianeti?

Come sempre, ho raccolto alcuni pensieri e creato degli indovinelli, quindi ti invito a proseguire.
Prima di cominciare, se hai tenuto da parte dallo scorso numero un Fruscello dell’Albero della Vita, o se vuoi cimentarti in una lettura un po’ impegnativa, vai al 2.
Altrimenti vai all’indice, al 3.

____________________2____________________

Completiamo il viaggio cominciato due numeri fa parlando di modelli di evoluzione del DNA.
È importante saper valutare la “distanza” fra stringhe di DNA per ricostruire la storia di una specie, perché è un indicatore della distanza temporale fra le specie attuali e il progenitore comune; vorrei qui farti riflettere proprio sulla natura delle modifiche al DNA. Se davvero il DNA è una stringa molto lunga di 4 simboli, allora eventi casuali potrebbero modificarla, lettera per lettera,

e queste mutazioni giocherebbero un ruolo fondamentale nella storia dei viventi, portando alla comparsa di nuove varianti e alla nascita nuove specie.
(Una nota si rende necessaria per non confondere il lettore. Naturalmente, per M. Shelley tutto ciò che riguarda il DNA è inventato, quindi non parla scientificamente, pur presentando con sorprendente precisione e realismo la maggior parte dei concetti, come accade quando parla di mutazioni. A riguardo, quelle di cui parla sono dette mutazioni puntiformi, dovute principalmente ad errori nella copiatura del DNA fra una generazione all’altra e ad agenti mutageni, come le radiazioni.
Comunque, la mancanza più grande nel ragionamento di Mary è il non considerare l’influenza della selezione naturale nei modelli di evoluzione del DNA: una mutazione che altera i geni sarà necessariamente esposta alla selezione naturale, con l’ambiente che sceglierà solamente alcune varianti; con il passare del tempo quindi saranno sì le mutazioni a modificare il DNA, ma sarà presente anche il giudizio della selezione: frammenti di DNA legati allo sviluppo di funzioni essenziali dell’organismo si modificheranno molto meno di altri, appunto perché essenziali.
Comunque, esistono parti del DNA su cui la selezione non agisce, o almeno agisce con proporzione trascurabile rispetto le mutazioni, e su quelli si possono applicare i modelli di cui parlerà Mary nel seguito, n.d.T.)

Si parte da due stringhe diverse, DNA di due specie attuali,

Un primo modo per stimare la distanza fra le due è il p-metodo, ovvero calcolare il numero di basi differenti e dividere per la lunghezza della stringa analizzata. Queste due sequenze quindi, che hanno 2 differenze su 8 posizioni totali, distano $$\frac{2}{8}=0.25$$ (più il numero è grande, più tempo è passato dall’epoca in cui le due specie non erano ancora divise). Questo però è un metodo troppo ingenuo; per capirne il motivo, è necessario guardare indietro nel tempo, al momento in cui le due specie non si erano divise… osserviamo il DNA del loro progenitore comune.

Quando le specie si dividono, i loro DNA cominciano a subire mutazioni differenti che si accumulano e portano con il tempo alle sequenze moderne.

Come si può vedere dal disegno, sono tanti i modi in cui possono verificarsi mutazioni, e tale pluralità di effetti si perde guardando solo il risultato finale, come si fa con il p-metodo. In questo caso, ad esempio, sono avvenuti 10 eventi di mutazione, quindi la distanza reale è $$\frac{10}{8}=1.25$$, non $$\frac{2}{8}=0.25$$, le due specie sono imparentate molto più alla lontana di quanto non sembrasse inizialmente!
Il problema è che non si può guardare la storia delle mutazioni dal progenitore ai tempi attuali perché gli unici DNA disponibili sono quelli delle specie attuali, ancora viventi.
Per questo motivo è necessario utilizzare dei metodi matematici che simulano l’evoluzione del DNA, mutazione dopo mutazione, le Catene di Markov; gli ingredienti alla base sono i seguenti:

• Una grandezza che si modifica nel tempo, anche casualmente. La stringa di DNA cambia perché mutano le basi, si sceglie quindi di studiare come si modifica nel tempo la singola base;

• Uno spazio degli stati. Scelta la grandezza, si individua l’insieme dei valori che questa può assumere. Nel nostro caso, una base può essere di 4 tipi, o stati, A, T, C, G. L’insieme $$\{A,T,C,G\}$$ è lo spazio degli stati;

• Una matrice generatrice, che contiene tutte le informazioni e le regole relative all’evoluzione degli stati. Ecco subito un esempio:

  $$ Q=\left(\begin{array}{cccc} -5 & 1 & 2 & 1\\ 2 & -4 & 1 & 1\\ 1 & 1 & -2 & 0\\ 0 & 0 & 1 & -1 \end{array}\right)$$

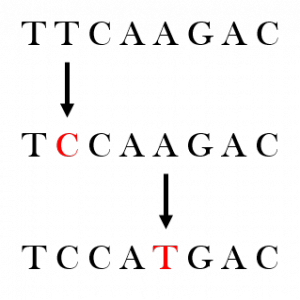
  Immaginiamo di voler simulare l’evoluzione della prima base del DNA della sequenza ancestrale $$TTCAAGAC$$; si parte da $$T$$. Il tempo passa finché non avviene una mutazione. Ma quanto tempo passerà, anche se sarà un tempo casuale?
  E poi, in cosa muterà $$T$$ e con che probabilità diventerà $$C$$, $$G$$ o $$A$$?
  La risposta ad entrambe le domande è la matrice generatrice, che ha 4 righe e 4 colonne, così da poter avere un valore per ogni coppia di stati, in ordine $$A,T,C,G$$. Vorrei farti notare che queste matrici hanno tutti gli elementi non negativi, ad esclusione di quelli sulle diagonali, e hanno la somma degli elementi di ogni riga pari a zero;
  

• Delle intensità di salto. Gli elementi diagonali della matrice, quelli negativi, rispondono alla prima domanda: ogni quanto tempo avverrà una mutazione?
  Prendi l’elemento diagonale relativo alla $$T$$, ovvero quello in posizione $$(2,2)$$, seconda riga, seconda colonna: $$-4$$. Cambiato di segno e invertito ($$\frac{1}{4}$$), quel numero indica “in media” quando la $$T$$ subirà una mutazione: il tempo reale sarà casuale, ma dobbiamo aspettarci un salto dopo circa $$\frac{1}{4}$$ (con l’unità di misura adeguata); se ci fosse stata una base diversa, come $$A$$, il salto ci sarebbe stato, in media, dopo meno tempo, $$\frac{1}{5}$$. Per i più esperti, sono parametri di variabili aleatorie esponenziali;

• Delle probabilità di transizione. I parametri precedenti non danno informazioni sull’effetto della mutazione, non aiutano cioè a capire in cosa le basi si trasformano; questo è lo scopo del resto della matrice, che risponde alla domanda: in cosa muterà una base e con che probabilità diventerà una delle altre tre?
  Guarda la riga riferita alla base $$T$$, ovvero la seconda,

  $$ \left(\begin{array}{cccc} 2 & -4 & 1 & 1\end{array}\right)$$,

  moltiplica ogni elemento per $$\frac{1}{4}$$ (il parametro riferito alla $$T$$ del punto precedente) e metti $$0$$ al posto del simbolo negativo,

  $$ \left(\begin{array}{cccc} \frac{1}{2} & 0 & \frac{1}{4} & \frac{1}{4}\end{array}\right)$$.

  Questa riga contiene l’informazione necessaria, con le basi ordinate come $$A,T,C,G$$.
  Quando avviene una mutazione della base $$T$$, si sceglierà infatti
  – con probabilità $$\frac{1}{2}$$ la base $$A$$,
  – con probabilità $$\frac{1}{4}$$ la base $$C$$,
  – con probabilità $$\frac{1}{4}$$ la base $$G$$.

Note queste regole, un modello di evoluzione del DNA si differenzia dall’altro dalla scelta della matrice generatrice, che può essere calibrata in base al tipo di analisi.
Ad esempio, potresti decidere che il tempo di salto è in media lo stesso per ogni base, e che pure le probabilità di salto sono tutte uguali, ottenendo

$$ \left(\begin{array}{cccc} -3\lambda & \lambda & \lambda & \lambda \\ \lambda & -3\lambda & \lambda & \lambda\\ \lambda & \lambda & -3\lambda & \lambda\\ \lambda & \lambda & \lambda & -3\lambda\end{array}\right);$$

oppure potresti scegliere parametri diversi per ogni base e per ogni probabilità di salto, ottenendo

$$\left(\begin{array}{cccc} \backslash & \beta\pi_{T} & \beta\pi_{C} & \alpha_{2}\pi_{G}\\ \beta\pi_{A} & \backslash & \alpha_{1}\pi_{C} & \beta\pi_{G}\\ \beta\pi_{A} & \alpha_{1}\pi_{T} & \backslash & \beta\pi_{G}\\ \alpha_{2}\pi_{A} & \beta\pi_{T} & \beta\pi_{C} & \backslash\end{array}\right)$$

(non ho scritto esplicitamente i termini in diagonale, che si possono ricavare sommando gli elementi della riga corrispondente).

Si conclude qui l’analisi cominciata con LUCA e PARSIMONIA nei volumi precedenti. La tua pazienza e attenzione verrà premiata, quindi lascia il Fruscello dell’Albero della Vita e raccogli quel Frutto dell’Albero della Vita, poi vai all’indice, al 3.

____________________3____________________

Indice.

  

Batteri, vai all’8;
Archaea, vai all’11;
Sanguisughe, cercali nel Volume I;
Polpi, cercali nel Volume II;
Coleotteri, vai al 6;
Rane, cercali nel Volume I;
Uomini, vai al 4;
Palme, cercali nel Volume II;
Muschi, cercali nel Volume II.

 

____________________4____________________

“All’interno dell’albero dei viventi non dimentichiamo che è presente anche l’Homo sapiens. Non ha un posto d’onore in cima all’albero, occupa una delle tante foglie, come le altre specie.”
A questo ragionamento mi ha portato il mio amico di penna Charles, di cui ti ho parlato, ecco un suo ritratto. Ed è ragionando sul nostro ruolo nel mondo che ho pensato a questo indovinello.

Se il nostro posto nel mondo non è da protagonisti, chi ha detto che questo mondo abbia ruolo di protagonista nell’Universo? È possibile che su un altro mondo esistano uomini? E se non gli uomini, sarà facile trovare qualche essere vivente?

Qual è la probabilità di trovare qualcuno per mostrare di non esser soli?

Che tu abbia o non abbia una risposta, vai al 5.

____________________5____________________

Prendiamo un pianeta lontano di cui non sappiamo nulla, eccetto che esiste. Ti ho domandato: ci sono uomini su quel pianeta?
E chi lo sa! O ci sono, o non ci sono, cinquanta e cinquanta.
E che si può dire delle balene? Lo stesso, sul pianeta c’è il 50% di probabilità che ci siano balene.
Quindi quante probabilità ci sono che su quel pianeta esistano uomini o balene? Proprio come il lancio di due monete, il 75%. E che dire dei topi? E dei grilli? E delle pulci? Dei pomodori, le mele, i batteri…? Se prendiamo in considerazione solamente 100 diverse forme di vita, le probabilità che almeno una di esse possa essere trovata sul pianeta sconosciuto sono quindi 99.999999999999999999999999999921%.
Se prendiamo in considerazione un pianeta di cui non conosciamo assolutamente niente, c’è quasi il 100% di probabilità che ci sia almeno una forma di vita. Chiaro no?

In termini matematici, ti sto parlando di probabilità composta, il calcolo della probabilità nell’osservazione di più eventi.
Se la probabilità che si verifichi un evento, come “presenza di esseri umani” o “presenza di balene” è $$ p $$, allora la probabilità che non si verifichi tale evento è data dal 100% (in frazione 1) meno la probabilità $$ p $$, ovvero $$ 1-p $$.

Dati due eventi, indipendenti fra loro, la probabilità che sia uno sia l’altro si verifichino è data dalla probabilità che si verifichi uno, $$p_1$$, moltiplicata la probabilità che si verifichi l’altro, $$p_2$$.
$$\mathbb{P}\left(\mbox{“Evento 1”}\,E\,\mbox{“Evento 2”}\right)=p_1 \cdot p_2$$.
Invece, la probabilità che uno oppure l’altro si verifichi è data dal 100% meno la probabilità che non se ne verifichi nessuno, né il primo né il secondo:
$$ \mathbb{P}\left(\mbox{“Evento 1”}\,O\,\mbox{“Evento 2”}\right)=1-(1-p_1)\cdot(1-p_2)$$.

Come esempio, calcoliamo la probabilità che lanciando due monete si ottenga almeno una testa. Ci sono quattro possibili riuscite: due teste; la prima testa e la seconda croce; la prima croce e la seconda testa; due croci.
Il risultato è favorevole tre volte su quattro, il 75%, infatti la probabilità che la prima non sia testa è il 50% (0.5), la probabilità che la seconda non sia testa è pure il 50%, quindi la probabilità che una o l’altra sia testa è  $$ 1 – 0.5 \cdot 0.5 = 0.75 = 75%$$ .

Estendendo il calcolo a un numero più elevato di eventi, la probabilità che almeno uno accada è data da:
$$ 1 – (1 – p_1)\cdot(1 – p_2)\cdot(1 – p_3)\cdot \ldots $$
Per esempio, lanciando 10 monete, la probabilità che almeno una volta esca testa è data da:
$$ 1 – 0.5 \cdot 0.5 \cdot \ldots $$ 10 volte, o
$$ 1 – 0.5^{10} = 1 – 0.0009765625 = 0.9990234375 = 99.90234375%. $$
Quando non sappiamo se qualcosa si realizzerà, c’è il 50% di probabilità che lo faccia.

Chiaramente ti ho ingannato con questo ragionamento, ma non ti spiegherò dov’è l’errore.
Ti invito a ragionarci, poi se vuoi leggere altri enigmi torna al 3; altrimenti vai al 15.

____________________6____________________

Scrive il reverendo William Paley nel suo Natural Theology:

Nell’attraversare un campo, supponiamo io inciampi in una pietra, e che mi venga chiesto come la pietra sia giunta sin lì; io probabilmente potrei rispondere che, fino a prova contraria, è stata lì da sempre, né sarebbe facile da dimostrare l’assurdità di tale ipotesi.
Supponiamo invece che io abbia trovato un orologio sul terreno, e che si indaghi su come sia possibile che l’orologio fosse in quel posto; sarebbe improbabile che io pensassi alla risposta di prima, cioè che, per quel che ne so, l’orologio potrebbe essere lì da sempre. L’orologio deve aver avuto un fabbricante: deve essere esistito, in qualche tempo e in qualche posto, un artefice, o artefici, che lo crearono per lo stesso scopo che noi al vederlo gli attribuiamo, che ne comprendevano la struttura e ne progettarono l’uso.

Non penso di essere d’accordo con la morale che l’autore vuole trasmettere con questo testo, ovvero la necessità di un “orologiaio” senziente, un essere intelligente (magari proveniente da un altro mondo), creatore della complessità nel mondo dei viventi. Non è questa comunque una rivista di filosofia della scienza, quindi ti parlo solo di un enigma che mi è venuto in mente leggendo tutto ciò; con questo gioco vorrei farti capire come complessità e intelligenza non siano così intuitivamente legate e come la prima possa insorgere da regole molto semplici. Ecco il problema:

Un coleottero vive su una scacchiera infinita composta da celle bianche e nere, e può essere rivolto verso una delle quattro direzioni della bussola: nord, sud, ovest, est. A ogni turno si sposta in avanti di una cella e segue tre semplici regole:

• Se finisce su una cella nera, ruota di 90° a sinistra;
• Se finisce su una cella bianca, ruota di 90° a destra;
• La cella che ha appena abbandonato cambia colore, da bianca a nera, o viceversa.

Ecco le prime mosse:
il coleottero parte rivolto verso est su una scacchiera completamente bianca;
la prima mossa lo porta in una casella bianca, mentre la casella da cui è partito diventa nera;

     

dato che di trova su una casella bianca, si gira verso destra, e ora è rivolto a sud;
questo lo porta a una nuova casella bianca, e la casella che ha abbandonata diventa nera.

     

Dopo poche mosse il coleottero inizia a visitare per la seconda volta caselle precedenti che sono diventate nere, e quindi gira a sinistra…
La mia domanda, particolarmente difficile, è: cosa succederà se lasciamo passare tanto tempo?

La soluzione è al 7.

 

____________________7____________________

Con il passare del tempo il movimento diventa piuttosto complicato, e con esso la disposizione delle caselle bianche e nere che il coleottero si lascia alle spalle. Poi le cose si fanno abbastanza caotiche per circa diecimila mosse.

Dopo ciò il coleottero è intrappolato in un ciclo in cui si ripete indefinitamente la stessa sequenza di 104 mosse, ma dopo ogni ciclo si ritrova spostato di due caselle in diagonale. Continua così per sempre, costruendo sistematicamente un’ampia “strada” diagonale.

Il protagonista del gioco è un coleottero, che qui non è niente più di un automa, alla stregua di un giocattolo a molla, ma guardando questo comportamento complesso, fatto di ordine proveniente dal caos, saremmo portati a pensare che sia stato intelligente.
La cosa curiosa è che, facendo altri esperimenti, ho trovato qualcosa di ancor più sorprendente. Se spargi sulla scacchiera un qualsiasi numero di finito di caselle nere prima che il coleottero si metta in moto, finisce ugualmente per costruire una strada. Può impiegarci più tempo, le sue mosse iniziali possono essere molto diverse, ma alla fine succederà comunque.

Ho proposto questo problema a molti matematici del mio tempo, ma sono tutti rimasti perplessi. Il coleottero finisce sempre per costruire una strada, qualunque sia la configurazione iniziale?
(Non è chiaro neanche ai matematici del mio tempo, n.d.T)

Se vuoi leggere altri enigmi torna al 3; altrimenti vai al 15.

 

____________________8____________________

Non è da molto che negli ambienti intellettuali è nato l’interesse verso quel tipo di organismi a cui ci riferiamo quando parliamo di germi. Per quel che ne sappiamo, i germi, i batteri, sono esseri piccoli e resistenti, che sanno vivere in condizioni ambientali difficili. Vi presento tramite un disegno come immagino siano i batteri, visti con un microscopio molto potente.

I batteri sono esseri semplici, che si riproducono per scissione binaria, e lo fanno in maniera molto rapida, una generazione ogni mezz’ora. (Ecco un ulteriore dato inventato da Mary, ma realistico, n.d.T). Con questo gioco voglio darti un’idea di cosa significhi un tempo di replicazione così veloce.
Immaginiamo che dopo ogni riproduzione i nuovi nati si posino gli uni sugli altri, a formare una torre molto esile; quanto tempo impiegheranno a raggiungere la Luna?

Immagino che un batterio sia “alto” circa un micrometro, ossia $$ 10^{-6} $$ m. La Luna dista circa 400000 Km, ossia $$ 4 \cdot 10^8 $$ metri.
Un suggerimento è cominciare a calcolare l’altezza della torre; inizialmente, al “passo 0”, sarà alta $$ 10^{-6} $$ metri, consistendo di un solo batterio; al “passo 1” la torre raddoppia d’altezza e ogni passo sarà alta il doppio del precedente.
Ti ripeto quindi la domanda: quanto impiegheranno a raggiungere la Luna?

La spiegazione completa è al 9, la soluzione al 10.

____________________9____________________

Puntiamo a risolvere il problema:
l’altezza dopo $$n$$ passi ($$n$$ riproduzioni), $$ h_n $$, è il doppio dell’altezza al passo precedente ($$h_n = 2 h_{n-1}$$),
quattro volte l’altezza di due passi prima ($$h_n = 4 h_{n-2} = 2^2 h_{n-2}$$),
8 volte quella di tre passi prima ($$h_n = 8 h_{n-3}=2^3h_{n-3}$$).

Si può tornare indietro $$n$$ volte (il numero di passi fatti fino a quel momento) e affermare che l’altezza $$h_n$$ è $$2^n$$ volte quella iniziale, $$ h_n = 2^n h_0$$.
Fortunatamente sappiamo il valore di $$ h_0 $$, altezza iniziale, ossia $$10^{-6} m$$;
quindi dopo $$n$$ riproduzioni la torre sarà alta $$2^n \cdot 10^{-6} m$$ (2 riproduzioni, $$ 4 \cdot 10^{-6} m = 4 \mu m$$, 10 riproduzioni $$ 1,024 mm$$).
Dopo quante riproduzioni siamo sulla Luna? Quando $$n$$ è tale che

$$ 2^n \cdot 10^{-6} = 4 \cdot 10^8 $$

Risolviamo l’equazione esponenziale, trovando $$n$$. Ci sono due strade:

Tentativi: provare valori finché non si arriva alla soluzione (solitamente è una strada impraticabile, a meno di avere già un’idea del risultato. Se riuscite a risolvere per tentativi, bravi! Andate al 10);

 Logaritmi: esiste un modo agevole (ma va conosciuto) per risolvere il problema, questi sono i passaggi principali:

• Dividiamo entrambi i termini dell’equazione per 4, poi moltiplichiamoli per $$ 10^6 $$, ottenendo

$$ 2^{n-2} = 10^{14} $$

• Passando ai logaritmi si ottiene

$$ n-2 = \log_{2} 10^{14} $$

• Ovvero $$ n = 48,5 $$ circa, per eccesso 49.

Solamente 49 replicazioni! E quanto tempo? 49 volte per 30 minuti, ovvero circa 24 ore!
Vai al 10.

 

____________________10____________________

La soluzione del problema è sorprendente: in un solo giorno (poco più di 24 ore) la torre sarà alta quanto la Luna!
Se il risultato non ti stupisce molto, anche se si parla di sole 49 riproduzioni (si può criticare, a ragione, la troppa astrazione e incoerenza con la realtà: le creature non muoiono, si riproducono ad un tasso costante, riescono a salire uno sull’altro senza problemi, non mangiano, hanno risorse infinite, non ci sono predatori) immagina che, invece di un batterio ci sia un normale foglio di carta; potrei riformulare la domanda in: quante volte ripiegare su se stesso un foglio per arrivare sulla Luna? 42 volte!
Potresti provare realmente, ma sarebbe una missione senza speranza, non è possibile andare oltre la sesta o settima piega; non resta che fidarti dei calcoli.

Se vuoi leggere altri enigmi torna al 3; altrimenti vai al 15.

 

____________________11____________________

Il gioco che sto per proporti è nato come spunto di ragionamento, come risposta ad una delle domande che ti ho posto all’inizio di questo volume: siamo sicuri di essere la specie più adatta ad andare su altri mondi?
Io non credo, ed è per questo che ho inventato un organismo, il Pyrococcus furiosus, di cui ho fatto un disegno, qui sopra. Ho immaginato che tale specie sia parte di un regno di organismi ancestrali, che ho battezzato Archaea, che, come hai potuto leggere nell’albero genealogico (al 3), sia lontano geneticamente dagli eucarioti e gli organismi più complessi, ma non sia un batterio.
La mia specie è fatta di individui piccoli e resistenti, adatti a vivere in condizioni estreme, come le sorgenti termali, a temperature superiori a 100°C. È da un organismo come questo che mi aspetto la capacità di colonizzare un territorio alieno.
(Inutile dirvi che anche qui Mary ha solamente anticipato dei risultati realistici. In particolare, nel 1970 non esistono ancora vere evidenze sperimentali sull’esistenza degli Archaea, n.d.T).
Ecco quindi che ti presento questo gioco di colonizzazione:

Immaginiamo di avere un quadrettato che prosegue all’infinito in ogni direzione, con le caselle che possono essere colorate (un archaea) o bianche (terreno vuoto). Scelta una riga, che chiamiamo orizzonte, poniamo un archaea in ogni casella sotto l’orizzonte, nessun archaea sopra l’orizzonte:

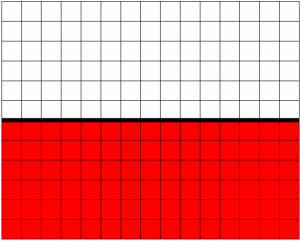
Gli archaea tentano di prevalere uno sull’altro, uccidono, muoiono, per accaparrarsi il posto più lontano possibile dall’orizzonte; avanzano muovendosi come nella dama, uccidendo un vicino in orizzontale o in verticale, scavalcandolo e ponendosi davanti, così (le caselle in giallo possono essere piene o vuote)

La mia domanda per te è la seguente: quale sarà la massima distanza dall’orizzonte che riuscirai a fargli raggiungere?
Quando sarai riuscito a risolvere i primi casi, ovvero far raggiungere la prima, la seconda, la terza e la quarta riga, potrai andare alla soluzione, al 12.

 

____________________12____________________

Raggiungere la prima riga è facilissimo, sono coinvolti solamente due archaea, con il primo che scavalca il secondo; anche raggiungere la seconda non richiede sforzi particolari, necessitando di solo 3 mosse e coinvolgendo solo due archaea. Raggiungere la terza e quarta riga è più complicato, ma il disegno qui sotto mostra quali sono gli archaea coinvolti (si possono utilizzare alternativamente quelli indicati con A o con B),

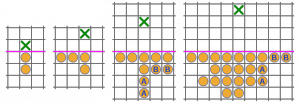
Il passo successivo è raggiungere la quinta riga. Prova, troverai la soluzione al 13.

____________________13____________________

La realtà è che non posso spiegarti come portare gli archaea in quinta riga, perché non c’è modo di farlo. Qualunque strategia si scelga, non è possibile che la colonizzazione del pianeta avanzi più di cinque passi, nonostante tu abbia a disposizione un numero grande a piacere di organismi! Non è un fatto di ambiente inospitale, è matematica!
La spiegazione completa, anche se complessa, è al 14.

Se vuoi leggere altri enigmi torna al 3; altrimenti vai al 15.

 

____________________14____________________

Leggi qui, poi se vuoi leggere altri enigmi torna al 3; altrimenti vai al 15.

 

____________________15____________________

E anche questo terzo numero qui si conclude. Spero ti sia piaciuto immaginare mondi lontani, perché io mi sono divertita. Ti aspetto per il prossimo numero, che sarà più articolato e… spiraliforme.
Mary

 (Come già detto, abbiamo già pubblicato il quarto e ultimo numero, che potete trovare qui. n.d.T)

 

Bibliografia

Enigmi e Giochi Matematici – Martin Gardner

Computational Molecular Evolution – Ziheng Yang
Il giardino nella macchina. Della vita artificiale – Claus Emmeche