Uno spinoff de “La Matematica Umida dell’Evoluzione”

THE LAST WOMAN

di Mary Shelley

VOL. II

____________________1____________________

Al lettore.

Bentornato,
di fronte a te c’è un nuovo ed innovativo volume di “The Last Woman”; ti consiglio vivamente di recuperare il precedente numero per non perdere nessun gioco o curiosità biologica (qui).
Se vuoi, puoi seguire la lettura e lasciarmi parlare di un’invenzione, di un’idea fantasiosa che ho avuto e che, teoricamente, mi permetterà di farvi comprendere un problema caro al mio “amico di penna”, Charles Darwin.

Nelle sue lettere mi parla di Teoria della Selezione naturale, spiegandomi come, con il passare delle epoche, le specie viventi si siano adattate al proprio ambiente, fino a generare la diversità del Mondo attuale; certo è che un pensiero lo turba…

• gli esseri viventi accumulano variazione e sono differenti fra di loro, ed è per questo che possono adattarsi all’ambiente, dove sopravvive il più adatto;
• gli esseri viventi trasmettono le loro caratteristiche ai propri discendenti;

Deve quindi esistere all’interno di ogni organismo un contenitore delle sue informazioni, che con il tempo si possa modificare e trasmettere alla prole… ma cosa?
Come si immagazzina l’informazione di un vivente? Come si trasmette? Chi è in grado di farlo?

È per questo che ho speculato, ho immaginato esista una molecola che ho battezzato… DNA.
(Non è ovviamente una speculazione, perché nel 1953 Watson e Crick nel loro articolo su Nature presentarono il celebre modello a doppia elica; leggi il primo numero di Matematica Umida, n.d.T.)
Nella mia mente, tale molecola dovrà contenere un codice, diverso per ogni organismo ma simile fra organismi della stessa specie…un “numero identificativo” di ognuno.
Tale codice era presente nel progenitore ancestrale dei viventi e si trasmette invariato da padre in figlio, generazione dopo generazione.
O, meglio, quasi invariato, perché ogni copia avrà poche modifiche che con il tempo si accumuleranno. Organismi prossimi da un punto di vista evolutivo dovranno necessariamente avere DNA simili…
Ora puoi continuare la lettura, oppure andare direttamente agli enigmi di questo volume, l’elenco dei quali puoi trovare al 2.

Grazie al DNA posso mostrarti un altro modo per ricostruire gli alberi genealogici dei viventi. Lo scorso volume vi ho mostrato LUCA, oggi il gioco si chiama

PARSIMONIA o RASOIO DI OCCAM.

Immagina una specie animale, ogni membro ha DNA molto simile ad ogni altro. Ad un certo momento avviene un evento naturale che divide la specie in due popolazioni che si trovano a vivere in diversi ambienti; con il passare del tempo insorgeranno modifiche differenti nel DNA delle popolazioni (oggi sappiamo che sono date da mutazioni e dall’effetto della selezione, n.d.T.), modifiche che diverranno sempre più grandi finché non si potrà più parlare di un unico gruppo: sarà avvenuto un evento di speciazione. In una situazione come questa,

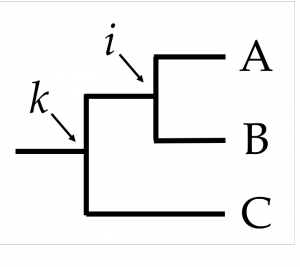
ci si aspetta quindi che i DNA delle specie A e B siano più simili fra loro di quanto lo siano con C.
Immagina quindi di avere a disposizione parte del DNA di varie specie, rappresentato come codice di due “lettere”, 0 e 1; il codice genetico che ho immaginato ha in realtà 4 lettere, che ho chiamato basi, ma con 0 e 1 è più semplice (sono proprio 4 le vere “lettere”, le basi azotate con sigla A, T, C, G, n.d.T.)

SPECIE A:     1 0 0 0
SPECIE B:     1 0 0 1
SPECIE C:     1 0 1 1

Tramite analisi comparata con specie più lontane a livello di parentela, possiamo ipotizzare che la specie ancestrale alle tre abbia avuto codice

ANCESTRALE: 0 0 0 0

Sono possibili tre diverse linee di discendenza:

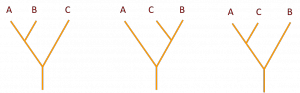
I DNA delle specie sono differenti perché sono avvenute modifiche nel tempo nelle singole “lettere”; per ognuno dei tre alberi si può calcolare il numero minimo di modifiche al DNA necessarie per portare dall’ancestrale alle forme attuali; riguardo al primo albero ad esempio

si può dire che sono necessarie 4 modifiche per raccontare la storia evolutiva delle tre specie.

Visto che immagino tali modifiche molto rare (il DNA deve trasmettersi quasi invariato da una generazione all’altra) decido che il vero albero di discendenza, o almeno il più probabile, è quello con meno modifiche avvenute nel DNA. In questo caso è il terzo albero, perché bastano 3 modifiche:

Ecco quindi PARSIMONIA o RASOIO DI OCCAM:

• si prendono un numero qualunque di DNA di specie diverse;
• si costruiscono tutti gli alberi di discendenza possibili;
• per ogni albero si conta il numero minimo di modifiche necessarie a passare dal progenitore alle specie attuali;
• si prende l’albero con il minor numero di modifiche.

Bel metodo, vero?
Se hai tenuto da parte dallo scorso numero un Seme dell’Albero della Vita, vai al 3.
Altrimenti vai all’indice, al 2.

____________________2____________________

Indice.

  

Batteri, cercali nel Volume III;
Archaea, cercali nel Volume III;
Sanguisughe, cercali nel Volume I;
Polpi, vai al 10;
Coleotteri, cercali nel Volume III;
Rane, cercali nel Volume I;
Uomini, cercali nel Volume III;
Palme, vai al 4;
Muschi, vai al 12.

____________________3____________________

Il metodo di parsimonia, seppur dotato della sua eleganza, ha un problema di complessità piuttosto rilevante. È necessario infatti passare in rassegna un gran numero di alberi per scegliere il migliore. Ma quanto grande?
Per due specie c’è un solo albero,

Possiamo aggiungere un ramo a quest’albero in 3 modi diversi, quindi con tre specie ci sono 3 differenti alberi,

Per ognuno dei tre alberi, possiamo aggiungere un nuovo ramo in 5 modi, quindi con 4 specie possiamo costruire $$5\cdot 3=15$$ alberi,

Per 5 specie, ci sono $$7\cdot 5\cdot 3=105$$ alberi;
per 6 specie, $$9\cdot 7\cdot 5\cdot 3\cdot$$ e così via.
Se volessimo costruire un albero per n specie di organismi, allora dovremmo controllare ben

$$(2n-3)(2n-5)(2n-7)\ldots5\cdot 3$$

diversi alberi.
Tale numero, numero di Schroeder, può essere scritto in maniera compatta con la notazione del doppio fattoriale,

$$(2n-3){!!}$$

e cresce in maniera incredibile all’aumentare delle specie… è impossibile calcolare a mano il metodo di parsimonia quando si trattano quantità così grandi!
(e dato che il numero relativo a 50 specie ha lo stesso ordine di grandezza del numero di atomi di Idrogeno in tutto l’universo, è impossibile da calcolare anche con il più potente computer attuale, n.d.T.)
È necessario scegliere quindi altri algoritmi per costruire discendenze genetiche…

Quindi lascia il Seme dell’Albero della Vita e raccogli un Fruscello dell’Albero della Vita se vuoi sapere come costruire un modello di evoluzione del DNA, perché ne parleremo nel prossimo volume di The Last Woman.
Ora vai all’indice, al 2.

____________________4____________________

Spesso mi capita di immaginare situazioni e problemi non banali leggendo storie; questo che sto per porvi, ad esempio, è ispirato al romanzo d’avventura di Daniel Defoe “The Life and Strange Surprising Adventures of Robinson Crusoe” e alla pianta di Cocos nucifera (la palma da cocco)…

Cinque uomini ed una scimmia fecero naufragio su un’isola deserta e passarono il primo giorno a raccogliere noci di cocco per cibo. Poi le ammucchiarono tutte insieme e andarono a dormire.
Ma mentre tutti dormivano uno di essi si svegliò e pensando che il mattino dopo vi sarebbero stati dei litigi alla spartizione, decise di prendersi la sua parte.
Perciò divise le noci in cinque mucchi. Rimaneva una noce, che egli dette alla scimmia, poi nascose la sua parte e mise tutto il resto assieme.
Subito dopo un secondo uomo si svegliò e fece la stessa cosa. Anch’egli dette l’unica noce residua alla scimmia.
Uno dopo l’altro tutti e cinque gli uomini fecero la stessa cosa, ognuno prendendo un quinto del mucchio e dando l’unica noce in avanzo alla scimmia.
Alla mattina divisero le noci ed ognuno ottenne lo stesso numero; ne avanzava una, che venne data alla scimmia.
Naturalmente ognuno sapeva che mancavano delle noci, ma ognuno era colpevole come gli altri e così nessuno parlò.

Quante noci c’erano all’inizio?

Posso spiegarti il ragionamento in due modi differenti:
un modo completo, ma decisamente lungo e complicato, che può valere anche per problemi più generali, al 5;
un modo furbo e rapido, che utilizza delle trovate “brillanti”, valido solo per questo indovinello, all’8.
Se invece hai già in mente la soluzione, vai al 9 per controllare se è giusta.

____________________5____________________

Per ricavare il risultato possiamo impostare il sistema seguente:

N = 5A + 1
4A = 5B + 1
4B = 5C + 1
4C = 5D + 1
4D = 5E + 1
4E = 5F +1

in cui N è il numero totale di noci all’inizio, F è il numero di noci che ciascun uomo riceve al termine della spartizione, A, B, C, D, E sono il numero di noci prese da ciascun marinaio durante la notte ed infine il +1 indica la noce che viene ogni volta data alla scimmia.
Tutti i valori devono essere numeri naturali (1, 2, 3, …).
Sostituendo le variabili, dopo un po’ di conti si può ottenere l’equazione seguente:

$$ 4^5N=5^6F+5^6-4^6$$

ovvero

$$1024N=15625F+11529$$

A questo punto bisogna risolvere questa equazione di primo grado tenendo però presente che il risultato non deve essere qualunque, ma un numero naturale. Siamo nel regno delle equazioni diofantee. Al 14 ti insegnerò come risolverle in generale (non è una lettura semplice); se non vuoi inoltrarti nei dettagli, puoi andare a leggere l’altro metodo risolutivo, all’8, o direttamente la soluzione, al 9.

____________________6____________________

Andare a tentativi non porta quasi a nulla, a meno che non si abbia l’anticonvenzionale idea di cercare una soluzione di Noci negative.
È piuttosto semplice trovarla, una volta avuta l’intuizione, è -4 noci:
il primo marinaio trova -4 noci, ne toglie una da dare alla scimmia ($$-4-1=-5$$), prende la sua parte ($$-5/5=-1$$) e lascia lì le rimanenti (-4);
il secondo marinaio trova -4 noci, ne toglie una da dare alla scimmia ($$-4-1=-5$$), prende la sua parte ($$-5/5=-1$$) e lascia lì le rimanenti (-4);
il terzo marinaio…
-4 è una soluzione negativa che sicuramente non ha senso fisico e non è la vera soluzione. Sappiamo però che sommando 15625 si ottiene una nuova soluzione valida,
$$ -4+15625=15621$$.
Vai al 9.

____________________7____________________

Furbo! Questa non è l’unica soluzione al problema, un’altra è 15. È proprio lì che devi andare.

____________________8____________________

La prima idea che verrebbe in mente è quella di “procedere a tentativi”, ad esempio con delle monete al posto delle noci di cocco; in questo caso però tale metodo non sembra aiutare poi molto, provare per credere. Aiuta invece semplificare il problema, immaginiamo quindi che i naufraghi siano 2:

Due uomini ed una scimmia fecero naufragio su un’isola deserta e passarono il primo giorno a raccogliere noci di cocco per cibo. Poi le ammucchiarono tutte insieme e andarono a dormire.
Ma mentre tutti dormivano uno di essi si svegliò e pensando che il mattino dopo vi sarebbero stati dei litigi alla spartizione, decise di prendersi la sua parte.
Perciò divise le noci in due mucchi. Rimaneva una noce, che egli dette alla scimmia, poi nascose la sua parte e mise tutto il resto assieme.
Subito dopo il secondo uomo si svegliò e fece la stessa cosa. Anch’egli dette l’unica noce residua alla scimmia.
Alla mattina divisero le noci ed ognuno ottenne lo stesso numero; ne avanzava una, che venne data alla scimmia.

Questa versione semplificata si risolve a tentativi, infatti la soluzione è…
Vai a quel numero.

____________________9____________________

I naufraghi si sono dati molto da fare, dato che in una giornata hanno raccolto ben 15621 noci!

Se vuoi leggere altri enigmi torna al 2; altrimenti vai al 16.

____________________10___________________

Spesso mi capita di immaginare situazioni e problemi non banali leggendo storie; questo che sto per porvi, ad esempio, è ispirato al romanzo d’avventura di Daniel Defoe “The Life and Strange Surprising Adventures of Robinson Crusoe” e un ordine di animali marini, gli Octopoda (i polpi)…

Robinson si trova di fronte un polpo, appena pescato, che ancora si contorce sugli scogli. L’uomo si interroga: perché il polpo ha proprio 8 tentacoli?
E tu? Sai la risposta?
Quando vuoi, vai all’11.

____________________11____________________

Davvero sai perché un polpo ha 8 tentacoli? Io no, però dovrà avere una spiegazione evolutiva.
Non voglio naturalmente spiegarti quello che non so, ma mostrarti come solitamente mi comporto davanti ad un quesito del genere; la prendo alla lontana…

Ci troviamo spesso di fronte ad eventi particolarmente “fortuiti”, quel tipo di situazioni che fanno esclamare “Che fortuna!” o “Non è possibile che accada!”, “Ci deve essere il trucco!”: un incontro inaspettato con una persona che non si vedeva da tempo, una vincita consistente ad un gioco d’azzardo…
Comunque, esistono vari livelli di “improbabilità” e non tutte le “fortune” sono rare allo stesso modo; il nostro “Non è possibile che accada!” è a volte dettato dal non comprendere pienamente le cause dell’evento; come se si conoscesse l’epilogo di un racconto, ma non l’introduzione, lo svolgimento, i colpi di scena… il finale, di per sé assurdo, acquisirebbe senso una volta conosciute tutte le vicende che gradualmente hanno portato ad esso.
Allo stesso modo, note le cause di eventi inizialmente ritenuti “rarissimi”, si smetterà di parlare di eventi fortunati e si comincerà a chiamarli coincidenze non troppo sorprendenti, o magari naturali conseguenze dei fatti.

Ti mostro un gioco (mentale) che ho inventato: immagino di entrare in una stanza e trovare su un tavolo 4 dadi, tutti che indicano 6,

Prima di esclamare “Che fortuna!” rispondiamo alla domanda: “Come hanno fatto a finire lì?”, così da chiarire i vari livelli possibili di improbabilità, ai quali ho dato un nome…

1. DISEGNO INTELLIGENTE.
   Se qualcuno prima di me avesse tirato i 4 dadi, poi una folata di vento li avesse girati proprio tutti sul 6, allora sì che avrei fatto bene a dire “Che fortuna!”; starei guardando il risultato di un evento rarissimo, un “miracolo”!
2. UNA FORTUNA PAZZESCA.
   Se qualcuno prima di me avesse tirato i 4 dadi e avesse ottenuto tutti 6, ci crederei un po’ più, ma avrei comunque avuto ragione a ritenerlo un evento molto improbabile.
3. ACCIDENTE CONGELATO.
   Se qualcuno prima di me avesse tirato in realtà più di 4 dadi, ottenendo i quattro 6, ma riordinandoli per contare avesse urtato il tavolo facendo cadere tutto tranne i 6, posizionati al centro per caso, non mi sorprenderebbe più il risultato in sé (piuttosto mi sembrerebbe improbabile il maldestro incidente).
4. PSEUDO COLLO DI BOTTIGLIA.
   Se qualcuno prima di me avesse tirato più di quattro dadi truccati, tenendo sul tavolo solamente i 6, non penso sarei stupita più di tanto dal risultato davanti ai miei occhi.
5. COLLO DI BOTTIGLIA.
   Se qualcuno prima di me avesse tirato più di quattro dadi non truccati, ma molti più del caso precedente, tenendo solo i 6, non mi stupirebbe affatto di vedere un risultato di 4 sei.
6. NECESSITÀ DETERMINISTICA.
   Se qualcuno prima di me avesse preso quattro dadi e li avesse posizionati volontariamente tutti sul 6, il mio “Che Fortuna!” non avrebbe avuto proprio senso!

Così un singolo evento può essere raro, una casualità, o comune, dipende dalle cause. Tale riflessione è valida anche in ambito biologico: ripetiamo il gioco dei 4 dadi con il polpo.
“Perché un polpo ha proprio 8 tentacoli?”

1. DISEGNO INTELLIGENTE.
   Se non ci fosse una vera ragione che spieghi proprio il numero 8? Se fosse stata solamente una scelta volontaria di qualcuno (alieni?) a cui piaceva il numero 8?Spiegazione improbabile, decisamente.

2. UNA FORTUNA PAZZESCA.
   Se ad un certo istante della storia una combinazione di eventi incredibilmente rari, come caduta di meteoriti, aumento esponenziale di predatori, stravolgimenti climatici, avessero decimato le popolazioni di antenati dei polpi lasciando solamente gli individui con 8 tentacoli?
   Tutto può essere, ma propendo più per una spiegazione evolutiva.
3. ACCIDENTE CONGELATO.
   Immaginiamo fossero esistiti tanti antenati dei polpi, con numero di tentacoli variabili. Se fosse occorso un evento particolarmente tragico e avesse devastato la popolazione, tanto da lasciar vivi solo pochi esemplari? Qualcuno sarebbe dovuto rimanere, ad esempio quelli da 8 tentacoli.
   Questa spiegazione, seppur improbabile, non è assurda in generale. Per questo evento in particolare comunque, mi aspetterei qualcosa di meno casuale.
4. PSEUDO COLLO DI BOTTIGLIA.
   E se le tante varianti di polpi con numero diverso di tentacoli, con il passare del tempo, si fossero logorate, a causa di coincidenze sfortunate o solo la casualità della vita?
   Il polpo con 8 tentacoli sarebbe quindi una delle varianti migliori, non in assoluto la migliore, ma sicuramente la più fortunata.
5. COLLO DI BOTTIGLIA.
   E se alcune varianti non fossero proprio esistite? Ad esempio, se a causa delle simmetrie (leggi qui per sapere qualcosa in più sulle simmetrie nel mondo vivente, n.d.a.) non fossero mai esistite varianti con tentacoli dispari? E se fra tutte le varianti possibili a tentacoli pari fosse stata selezionata quella da 8 perché le altre avevano dei problemi? Ad esempio un polpo con 4 tentacoli sarebbe troppo lento nei movimenti, o un polpo con 10 tentacoli li troverebbe ingombranti.
   La varietà attuale, con 8 tentacoli, sarebbe resistita fino ad oggi perché la più adatta, non per qualche fortuna. Questo tipo di spiegazioni evolutive dovrebbero esser prese seriamente.
6. NECESSITÀ DETERMINISTICA.
   E se quella con 8 tentacoli fosse l’unica conformazione possibile? E se le leggi della fisica decretassero che quello è l’unico modo, e quindi necessariamente così doveva avvenire?
   Sarebbe una spiegazione inattaccabile, non casuale in nessun modo, ma non penso che questo sia mai il caso di un evento di Evoluzione.

La realtà non è naturalmente fra le opzioni presentate, non è così superficiale, ma questo è solo un gioco sulle “improbabilità”, grazie al quale puoi provare a cercare la soluzione da solo!

Se vuoi leggere altri enigmi torna al 2; altrimenti vai al 16.

____________________12___________________

Spesso mi capita di immaginare situazioni e problemi non banali leggendo storie; questo che sto per porvi è ispirato al romanzo d’avventura di Daniel Defoe “The Life and Strange Surprising Adventures of Robinson Crusoe” e ad una divisione di piccole piante, le Bryophyta (i muschi)…

 

La solitudine del naufrago fu terribile, tanto che per un periodo il suo miglior amico fu del muschio. Robinson intratteneva lunghe conversazioni, e trattava con lui temi complessi, interrogandosi pure sul loro rapporto d’amicizia: come è possibile che due specie così diverse vivano sulla stessa Terra?
Questa è la domanda che vi faccio, se le mutazioni che portano alle varie specie accadono molto raramente, come possono portare a cambiamenti così drastici?
Vai al 13.

____________________13____________________

La mutazione è sì un evento raro, ma non così tanto se confrontato con molti individui e con un tempo molto lungo; valutiamo a spanne, senza basarci su valori precisi.
Scegliamo un organismo abbastanza complesso, come muschio, o un essere umano e stimiamo che ad ogni generazione avvenga, in media, una mutazione nel suo codice genetico. Per come ho immaginato il DNA, dovrà essere suddiviso in tanti pezzi, che chiamo geni, ognuno addetto a generare una diversa caratteristica dell’individuo; per me, ne dovrebbero esistere almeno 25000…

(Lei sta inventando, ma in modo naive sta fornendo dati credibili, visto che il nostro DNA è composto da circa 25000 geni, che portano principalmente alla formazione delle proteine. Comunque, i geni sono una piccola parte del genoma completo, tanto che, anche se nonostante gli accurati meccanismi di “controllo qualità” avvengano circa 150 mutazioni ogni generazione, solo una avviene nei geni, n.d.T.)

Questo vuol dire che, se scegliamo un gene, in media ogni generazione avverranno $$ 4\cdot10^{-5} $$ mutazioni in quel gene, uno su quattrocentomila, un numero piccolissimo.
Se però prendiamo una popolazione di un milione di individui, quel gene sarà mutato in circa 40; e se consideriamo 1000 generazioni, saranno avvenute in media 40000 mutazioni…
E poi, quando una mutazione si presenta, entrano in gioco l’ereditarietà e la selezione naturale, e quindi le modifiche potrebbero aumentare nella popolazione in tempo breve (relativamente).

Anche l’evento più raro si verifica, se passa tempo a sufficienza!
Se vuoi leggere altri enigmi torna al 2; altrimenti vai al 16.

____________________14____________________

Leggi qui, poi puoi andare a leggere l’altro metodo risolutivo, all’8, o la soluzione, al 9.

____________________15___________________

Esatto, con solo due naufraghi 15 è una soluzione del problema.
Il primo ne prende 7, ne dà una alla scimmia, il secondo ne prende 3, una alla scimmia, ne avanzano 3, una a testa più una alla scimmia.
Eppure 15 non è LA soluzione del problema, è solo UNA soluzione, come lo è ad esempio 7

Poiché dividiamo la somma per 2, tre volte, se sommiamo ad una soluzione un numero che è divisibile per 2 tre volte, ossia $$2^3=8$$ otteniamo una nuova soluzione. 15 è una soluzione, quindi anche $$15+8=23$$ lo è.

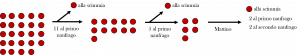
Lo stesso ragionamento è valido per il problema con 5 marinai.
Poiché dividiamo le noci per 5, sei volte, otteniamo una nuova soluzione ogni volta che sommiamo $$5^6=15625$$ ad una soluzione già nota.
Il problema però resta, va trovata una soluzione, per questo ti invito ad andare al 6.

____________________16___________________

In questo numero ci sono stati meno indovinelli, nel senso più tradizionale del termine, ma non ti aspetterai certo ogni numero uguale al precedente! Nel prossimo numero, ad esempio, parleremo di automi cellulari, quindi ti aspetto!
Mary

Bibliografia

Enigmi e Giochi Matematici – Martin Gardner
Algebra. Un approccio algoritmico – Giulia Maria Piacentini Cattaneo
Alle Origini della vita – Christian De Duve