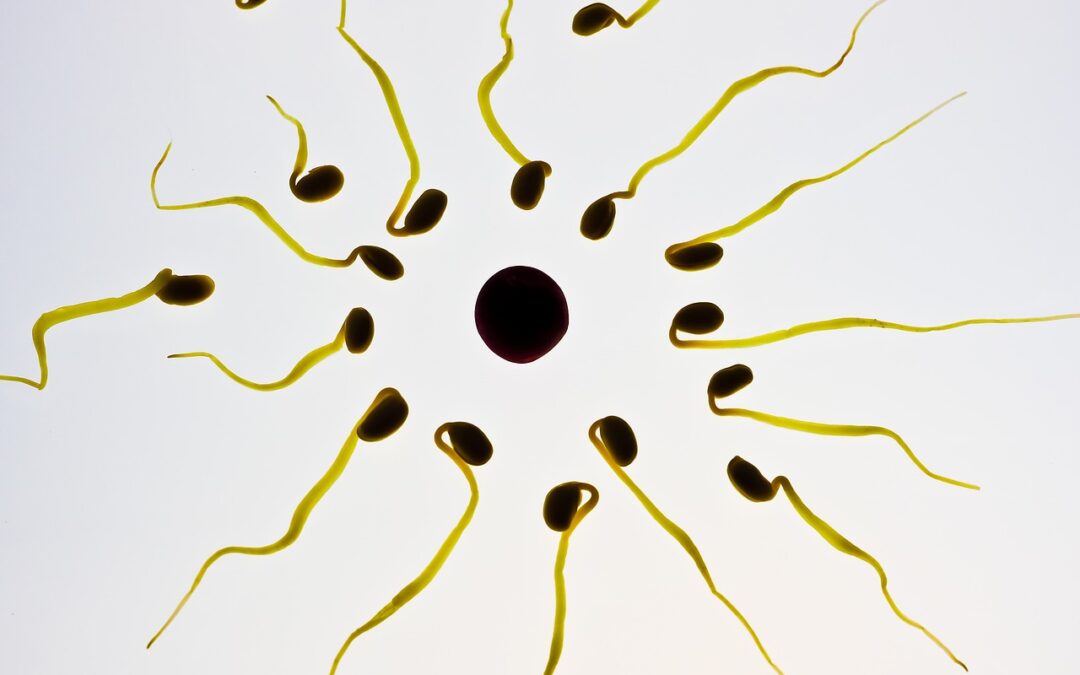
Si è osservato che gli spermatozoi umani seguono traiettorie regolari, ma molto più complesse, aventi la forma di eliche spiraleggianti. Un nuovo modello matematico cerca di spiegare meglio il moto di questi importanti microorganismi. Ne avevamo già dato la notizia qui, adesso vi proponiamo un approfondimento di Antonio DeSimone, grande esperto del movimento “dei piccoli nuotatori”.
La motilità cellulare è alla base di molti processi biologici di importanza fondamentale per la vita. Dalla migrazione delle cellule metastatiche, alla risposta del sistema immunitario, agli spermatozoi che nuotano nel loro viaggio alla ricerca di un uovo da fertilizzare, la motilità cellulare è presente nel destino degli esseri umani, dall’alfa all’omega.
L’articolo “Coarse-Graining the Fluid Flow around a Human Sperm” di K. Ishimoto e altri [1 ]K. Ishimoto, H. Gadelha, E. Gaffney, D. Smith, and J. Kirkman-Brown: Coarse-Graining the Fluid Flow around a Human Sperm. Physical Review Letters 118, 124501 (2017) (nel seguito “Coarse-Graining”) di recente pubblicazione, descrive il moto indotto nel fluido circostante dal nuoto degli spermatozoi umani, e ha attirato notevole attenzione anche nella stampa generalista. Nonostante si tratti di un argomento già studiato in modo approfondito, le intricate traiettorie descritte dagli spermatozoi riservano ancora molte sorprese.

Animalcules osservati da Anton van Leeuwenhoek nel 1695.
Il nuoto si fonda sul principio di azione e reazione. Quando agita la sua coda, lo spermatozoo deve esercitare forze sul fluido circostante per spostarlo. Di conseguenza, è soggetto alla reazione del fluido, uguale e contraria, che può essere usata come forza propulsiva. Da questa osservazione elementare segue che esistono due approcci complementari per studiare le strategie di nuoto degli organismi unicellulari (unicellulari: quindi di dimensioni microscopiche). Si può fissare l’attenzione sul nuotatore, oppure sull’impronta che il nuotatore lascia nel moto del fluido circostante.
Seguendo il primo approccio, la descrizione matematica del nuoto è basata sulle equazioni del moto del nuotatore. Questo è messo in moto dalle forze che il fluido esercita su di esso. Dato che, alla scala dimensionale degli organismi unicellulari, le forze d’inerzia sono trascurabili, il nuotatore deve riuscire ad avanzare vincendo la resistenza del fluido in assenza di forze esterne. Questo è l’analogo traslazionale del problema della caduta del gatto (falling cat problem, o riflesso verticale del gatto): partendo da una qualsiasi orientazione, un gatto riesce a raddrizzarsi nel corso di una caduta atterrando sulle zampe, ruotando in assenza di coppie esterne. Questo è il dominio della Teoria Geometrica del Controllo, la scienza che rende ha reso possibile il controllo delle traiettorie dei veicoli spaziali, con il suo ricco arsenale di strumenti matematici (si veda, ad es., la voce di enciclopedia [2 ]A. DeSimone, F. Alouges, A. Lefebvre: Biological fluid dynamics, nonlinear partial differential equations Springer Encyclopedia on Complexity and Systems Science (2009) per una breve introduzione).
Nel secondo approccio, il problema del nuoto è formulato attraverso le equazioni della fluidodinamica, che governano il moto del fluido circostante. Questo è messo in movimento dalle forze che il nuotatore esercita su di esso.
Per presentare questo secondo approccio, immaginiamo un ipotetico nuotatore olimpico che esegue una bracciata nello stile rana, mantenendo però le gambe ferme in posizione estesa (si tratterebbe di un nuovo ipotetico stile olimpico, non proprio efficientissimo, a dire la verità). In una parte della bracciata, la fase di “potenza”, il nuotatore muove le braccia completamente estese, diciamo verso il basso, e queste sono spinte verso l’alto dalla reazione del fluido. La resistenza viscosa del fluido al moto del nuotatore tira allora gambe e corpo del nuotatore in direzione opposta, dunque verso il basso. A causa del moto, il nuotatore è soggetto a un dipolo di forze estensionale, che tende a stirarlo. Il nuotatore quindi (sempre per azione e reazione) tira l’acqua (è un puller).
Nella fase della bracciata di “recupero della forma”, le braccia si muovono verso l’alto ma sono ripiegate vicino al corpo, per minimizzare la resistenza viscosa del fluido. Se l’inerzia è trascurabile, come nel caso delle scale microscopiche di interesse per i nuotatori unicellulari, il nuotatore arretra leggermente, muovendosi verso il basso, e la situazione descritta in precedenza si ripete, ma a segni invertiti. Il nuotatore è compresso dall’azione del fluido, esercitando sull’acqua un dipolo di forze estensionale (è un pusher).
Considerando la media sull’intero ciclo che compone la bracciata, poiché le forze viscose sono maggiori nella fase di potenza, le caratteristiche di questa fase dominano rispetto a quelle del recupero della forma e il nuotatore è, in media, un puller.
Questa analisi semplificata dei flussi indotti dall’ipotetico nuotatore olimpico si applica abbastanza bene al caso della Chlamydomonas reinhardtii, un’alga biflagellata che nuota in linea approssimativamente retta grazie al battere simmetrico di due flagelli. Questi sono posti in posizione anteriore rispetto al corpo, arrotondato, ed eseguono una bracciata a rana pressoche’ perfetta. Batteri come Escherichia coli, invece, sono spinti dal moto rotativo di un fascio elicoidale di flagelli posto nella parte posteriore del loro corpo allungato. Asse di rotazione, asse del corpo e asse dell’elica sono tutti allineati e il batterio si muove lungo una traiettoria ancora approssimativamente rettilinea (almeno nell’intervallo di tempo che separa due brusche virate, ottenute con una caratteristica manovra di `tumble’ effettuata invertendo il senso di rotazione dei flagelli).
 Mentre i nuotatori unicellulari finora descritti procedono approssimativamente in linea retta, grazie alla simmetria del loro battito flagellare, gli spermatozoi umani seguono traiettorie regolari, ma molto più complesse, aventi la forma di eliche spiraleggianti. Per spiegare l’origine di queste traiettorie gli autori “Coarse-Graining” dimostrano che il flusso generato dal nuoto degli spermatozoi può essere assimilato a quello generato da due “triplette di forze lampeggianti” (blinking force triplets). Questo significa che il modulo delle forze di ciascuna tripletta varia nel tempo, seguendo una specie di danza di coppia nella quale le due triplette si scambiano periodicamente il ruolo di guida della coppia. In ciascuna tripletta, due delle forze generano un dipolo allineato con la direzione del moto, esattamente come nei casi precedenti. Il terzo elemento della tripletta contribiusce con una forza che ha una forte componente laterale, perpendicolare alla direzione del moto, spiegando così le deviazioni laterali dalla traiettoria rettilinea e, in ultima analisi, le spirali delle traiettorie. In altri temini, mentre la testa dello spermatozoo è, in media, spinta dal flagello, è anche periodicamente tirata indietro e spinta lateralmente: questo spiega le traiettorie elicoidali comunemente osservate.
Mentre i nuotatori unicellulari finora descritti procedono approssimativamente in linea retta, grazie alla simmetria del loro battito flagellare, gli spermatozoi umani seguono traiettorie regolari, ma molto più complesse, aventi la forma di eliche spiraleggianti. Per spiegare l’origine di queste traiettorie gli autori “Coarse-Graining” dimostrano che il flusso generato dal nuoto degli spermatozoi può essere assimilato a quello generato da due “triplette di forze lampeggianti” (blinking force triplets). Questo significa che il modulo delle forze di ciascuna tripletta varia nel tempo, seguendo una specie di danza di coppia nella quale le due triplette si scambiano periodicamente il ruolo di guida della coppia. In ciascuna tripletta, due delle forze generano un dipolo allineato con la direzione del moto, esattamente come nei casi precedenti. Il terzo elemento della tripletta contribiusce con una forza che ha una forte componente laterale, perpendicolare alla direzione del moto, spiegando così le deviazioni laterali dalla traiettoria rettilinea e, in ultima analisi, le spirali delle traiettorie. In altri temini, mentre la testa dello spermatozoo è, in media, spinta dal flagello, è anche periodicamente tirata indietro e spinta lateralmente: questo spiega le traiettorie elicoidali comunemente osservate.
Per giungere alla loro visione sintetica (coarse-grained, nel titolo del loro lavoro) della impronta del nuotatore su flusso indotto, gli autori utilizzano una combinazione di metodi classici e di strumenti moderni. Il flusso è descritto come sovrapposizione di soluzioni fondamentali (espansione di multipolo) delle equazioni di Stokes (le equazioni che descrivono la fluidodinamica alla scala degli organismi unicellulari). Tra queste, quelle che forniscono i contributi più rilevanti (i modi principali) vengono estratte con le techiche della Principal Component Analysis. Questa procedura di selezione può essere resa algoritmica e automatica: è dunque, in un certo senso, una tecnica di apprendimento automatico (machine learning).
I risultati in “Coarse-Graining” aprono la strada verso l’analisi sistematica della motilità di organismi unicellulari attraverso l’analisi dei flussi da essi indotti nel fluido all’interno del quale si muovono. Questi flussi indotti portano impresse le impronte del comportamento individuale (il battito flagellare) di un organismo, che ha spesso un importante significato biologico. Usando tecniche di apprendimento automatico, l’analisi può essere estesa, dal livello individuale di un solo organismo a quello delle popolazioni, dove emergono interessanti fenomeni collettivi (formazione di sciami, ordine orientazionale, fromazione di vortici e turbolenza battaerica, …). La speranza è quella di riuscire così a formulare modelli alla scala delle popolazioni, capaci però di conservare la specificità biologica proveniente dalla dinamica cellulare dei singoli individui.
Antonio DeSimone
mathLab Director, SISSA Trieste
Immagine di copertina: Foto di Thomas Breher da Pixabay
Note e riferimenti
| ⇧1 | K. Ishimoto, H. Gadelha, E. Gaffney, D. Smith, and J. Kirkman-Brown: Coarse-Graining the Fluid Flow around a Human Sperm. Physical Review Letters 118, 124501 (2017) |
|---|---|
| ⇧2 | A. DeSimone, F. Alouges, A. Lefebvre: Biological fluid dynamics, nonlinear partial differential equations Springer Encyclopedia on Complexity and Systems Science (2009) |