Una mini-serie a cura di Gabriele Belegni, dove esploreremo i concetti principali di una delle branche più affascinanti della matematica: la topologia. Cercheremo di scoprire le motivazioni e le idee che hanno spinto ad introdurre certi concetti concentrandoci sull’aspetto intuitivo piuttosto che su quello formale. Oggi conosceremo molti spazi topologici, e capiremo meglio perché questa disciplina è considerata così utile e potente. Trovate tutte le puntate su questa pagina.
Nelle scorse puntate abbiamo visto che la topologia studia come possiamo deformare gli spazi topologici tramite delle particolari trasformazioni, gli omeomorfismi. Prendiamoci una pausa dai nuovi concetti e guardiamo un po’ di esempi, sia per dare un’immagine concreta a ciò di cui stiamo parlando, sia perché a mio parere sono carini da vedere.
Partiamo con cose facili da visualizzare. Triangoli, quadrati, pentagoni, insomma tutti i poligoni regolari e non che potete immaginare sono spazi topologici, così come lo sono tutte le coniche (circonferenze, ellissi, parabole e iperboli). Non solo tutti i poligoni sono spazi topologici, ma sono anche tutti omeomorfi tra di loro: senza stare a cercare la formula matematica, si vede facilmente che possiamo deformare, senza strappare o incollare pezzi, un quadrato su, ad esempio, un triangolo e che si può fare altrettanto facilmente il procedimento inverso. Questa cosa può poi essere fatta tra due qualunque poligoni del piano. Allo stesso modo, una circonferenza e un’ellisse sono sempre omeomorfe, in fondo un’ellisse è solo una circonferenza un po’ schiacciata, e tutte le circonferenze sono omeomorfe tra di loro (basta “tirarle” un po’ per far coincidere i raggi), stessa cosa per le ellissi. Non solo, ma anche tutte le curve chiuse semplici (cioè senza autointersezioni) sono omeomorfe tra di loro e omeomorfe alla circonferenza. Quindi, dato che spazi omeomorfi sono equivalenti in topologia, la circonferenza di raggio 1, che viene chiamata \(S^1\), rappresenta in un certo senso tutte le curve chiuse semplici.
I cerchi sono tutti omeomorfi tra loro e sono omeomorfi a tutti gli altri poligoni. Le parabole non sono omeomorfe né ai poligoni né alle altre coniche, infatti sono curve aperte e infinite, e per deformarle su ad esempio una circonferenza dovremmo necessariamente incollare due parti della parabola, cosa che non vogliamo fare in topologia. Una cosa analoga accade per le iperboli, che non solo sono infinite, ma anche fatte da 2 pezzi.
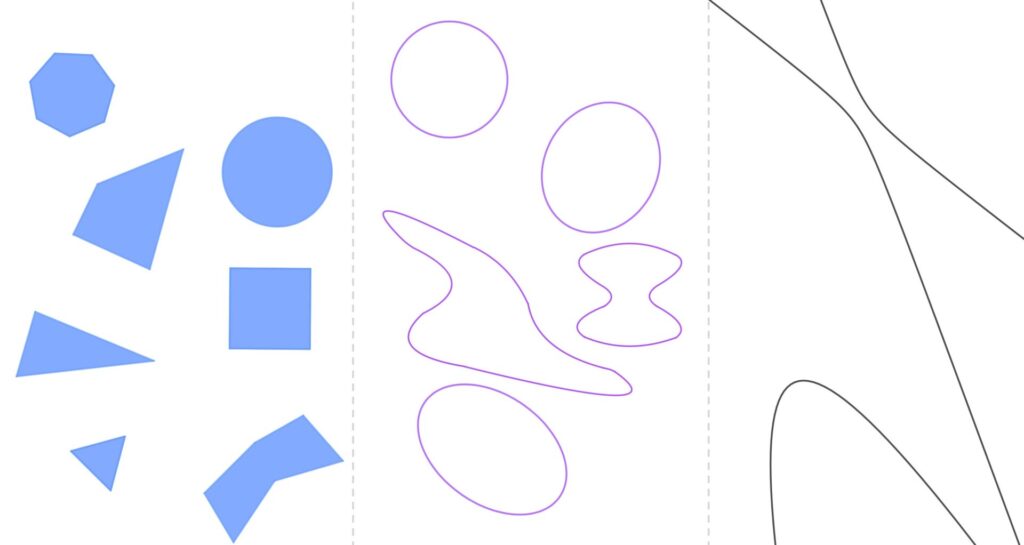
Alcuni spazi topologici nel piano
In modo molto simile a prima, tutti i solidi (quindi oggetti tridimensionali) sono spazi topologici e sono omeomorfi tra di loro e a una palla, mentre non sono omeomorfi ad esempio alla sfera (con sfera si intende sempre superficie sferica, quindi senza la parte dentro per capirci), che viene chiamata \(S^2\). Anche tutte le quadriche sono spazi topologici, ma non sempre sono omeomorfe. Ovviamente sono poi spazi topologici la famigerata tazza e la ciambella, che in matematica viene chiamata toro e viene indicata con \(T^2\).


Una sfera, un toro ed un iperboloide
Veniamo ora allo spazio topologico più semplice e a noi familiare: \(\mathbb{R}^n\) con la topologia euclidea. Detta così sembra tutto tranne che semplice e familiare, ma lasciate che mi spieghi. Dunque, \(\mathbb{R}\) è la retta, \(\mathbb{R}^2\) è invece il piano, quindi un qualcosa a 2 dimensioni (lunghezza e larghezza), mentre \(\mathbb{R}^3\) è lo spazio tridimensionale, quello in cui viviamo, l’Universo se volete, appunto lo spazio a noi più familiare. Ecco, \(\mathbb{R}^n\) è semplicemente lo spazio a \(n\) dimensioni, una cosa utilissima e fondamentale per noi matematici perché ci permette di lavorare comodamente anche quando entrano in gioco tante variabili. Va bene, ma cos’è la topologia euclidea? È la topologia i cui aperti sono le cosiddette bocce, cioè intervalli aperti nella retta, cerchi aperti (senza il bordo) nel piano, palle aperte nello spazio e loro analoghi in dimensione superiore.
Abbiamo già accennato a \(S^1\), la circonferenza unitaria (cioè di raggio 1), un oggetto bidimensionale, e alla sfera unitaria \(S^2\), tridimensionale. In maniera analoga, chiameremo \(S^n\) la “sfera” a \(n+1\) dimensioni, cioè lo spazio topologico fatto da tutti i punti di \(\mathbb{R}^{n+1}\) a distanza 1 dall’origine degli assi. Badate bene: quando si parla di \(S^n\) la si intende quasi sempre come spazio topologico a sé stante, dimenticandosi del fatto che si trova dentro \(\mathbb{R}^{n+1}\). Giusto per completezza, \(S^0\) è fatto da tutti i punti della retta a distanza 1 dall’origine (lo 0), quindi \(S^0\) è la coppia \(\{-1,1\}\). Legato a \(S^n\) è poi \(B^n\), la boccia \(n\)-dimensionale, quindi lo spazio fatto da tutti i punti di \(\mathbb{R}^n\) a distanza minore o uguale a 1 dall’origine. \(B^1\) è l’intervallo chiuso \([-1,1]\), \(B^2\) il cerchio unitario, \(B^3\) la boccia tridimensionale e così via.
Altri esempi più “esotici” di spazi topologici sono quelli che vengono più usati come immagini per questa materia, quali la bottiglia di Klein, il nastro di Möbius, i grafi, i nodi e, in un senso un po’ più particolare, le reti neurali, e potrei andare avanti ancora.
La bottiglia di Klein è una superficie simile a quelle che già conosciamo (sfera, cubo, ecc…), ma a differenza di esse questa vive nello spazio a 4 dimensioni, che quindi non riusciamo a visualizzare o immaginare propriamente. È una superficie senza bordo non-orientabile, cioè una superficie della quale non riusciamo a distinguere una parte “interna” ed una “esterna” (cosa fattibile, ad esempio, con una sfera). Quella che vedete nell’immagine sotto è una sua immersione nello spazio tridimensionale, cioè una sua versione a 3 dimensioni non del tutto corretta, ma almeno visualizzabile. In particolare badate che nello spazio a 4 dimensioni la bottiglia di Klein non si autointerseca, cosa che invece fa la sua versione a 3 dimensioni.
Il nastro di Möbius è forse una delle figure più famose, è anch’essa una superficie non orientabile ma, a differenza della bottiglia di Klein, la rappresentazione tridimensionale che vediamo è veritiera. Potete realizzare un nastro di Möbius anche voi: prendete una strisciolina di carta, fate fare mezzo giro su se stesso ad un estremo tenendo fermo l’altro e poi incollateli, ecco che avete il vostro nastro di Möbius. Una sua proprietà interessante è che se iniziate a camminare lungo la sua superficie, dopo un giro completo vi ritroverete sì nello stesso punto, ma dall’altra parte del nastro, a testa in giù!
I nodi sono poi l’oggetto di studi di un’altra branca della matematica, la teoria dei nodi, che vi invito caldamente ad esplorare, mentre i grafi sono un’oggetto incredibilmente utile per modellare innumerevoli situazioni, dalla logistica all’economia, e le famose reti neurali possono essere studiate con l’aiuto della topologia. Ah e dimenticavo le funzioni! Tutti i grafici di tutte le funzioni ad un qualunque numero di variabili sono spazi topologici.

A sinistra, la bottiglia di Klein [1]. In alto al centro un nastro di Möbius [2], in blu due esempi di nodi e in basso a destra il grafico di una funzione (\(x sin(x)\))
A vedere tutti questi esempi, gli spazi topologici sembrano tantissimi! Ed è proprio così, è questa la potenza della topologia: la sua generalità, la sua capacità di trattare una marea di oggetti molto diversi tra di loro, che la rende applicabile in altrettanti contesti altrettanto variegati.
Nel titolo non vi ho mentito (non troppo): tutte le cose che vedete attorno a voi, la sedia, il vostro telefono, il vostro gatto, tutto quanto è uno spazio topologico, anche voi lo siete. La spiegazione sta nella definizione di sottospazio topologico: non sarò io a darvela, anche perché avevamo detto che oggi avremmo parlato solo di esempi. Vi basti sapere che dalla definizione segue che ogni sottoinsieme di uno spazio topologico è a sua volta spazio topologico, quindi ogni parte, ogni pezzetto piccolo o grande che potete prendere dentro uno spazio topologico si comporta a sua volta come uno di essi. Così, dato che l’Universo, lo spazio tridimensionale in cui viviamo, cioè \(\mathbb{R}^3\), è uno spazio topologico, ogni cosa che trovate dentro l’Universo sarà a sua volta spazio topologico. Carino eh?
Bene, con questi esempi in mente possiamo proseguire la nostra chiacchierata sulla topologia; nella prossima puntata riprenderemo quanto accennato la volta scorsa: le proprietà topologiche. Ci vediamo lì!
4 – continua
Images credits:
[1]: Tttrung, Klein bottle made with gnuplot 4.0., https://commons.wikimedia.org/w/index.php?curid=960446
[2]: Fropuff, vectorized MobiusStrip-01.png, https://commons.wikimedia.org/w/index.php?curid=6610157























