Tornano le Ripetizioni di Davide Palmigiani. Questa volta si parla di regali e di “Secret Santa”.

Mi serve una mano.

Una mano per cosa?

Ho l’impressione che ci sia qualcosa di sbagliato ma non riesco a capire cosa.

Ma di che stai parlando?

Sì sì, c’è sicuramente qualcosa di sbagliato, tu con le tue “tecniche” matematiche sicuramente sai come uscirne.

Ma di che stai parlando? Non sono qui per le ripetizioni?

Ma che ripetizioni! Fra poco è Natale, ho un problema con i regali!

Che problema? Non sai a chi farlo? E io come ti aiuto?

No, no. Domani ci vediamo con gli amici e vogliamo dividerci i regali con Babbo Natale segreto, hai presente?

Ah sì, l’ho fatto anch’io con i miei, di amici. Ognuno riceve un bigliettino casuale con il nome della persona a cui fare il regalo, così invece di farlo a tutti, lo fa solo a uno, e tutti ricevono un regalo.

Esattamente, solo che non trovo un modo per assegnare i regali che mi soddisfi pienamente.

E perché no? Il modo classico non va bene? Spiega spiega…

Be’, solitamente ognuno scrive un biglietto con il suo nome, si mettono tutti in un sacchetto, poi a giro si pesca…

…e se ti capita di pescare il tuo lo rimetti dentro e ne peschi un altro.

Eh, e non ti sembra ingiusto? Può capitare che l’ultimo a pescare prenda proprio il suo nome. Con chi lo cambia? Si deve fare tutto da capo?

Non mi sembra proprio il peggiore dei problemi sai? Però hai ragione. Più che altro, questo metodo “classico” ha un ulteriore problema.

Vedi che ho ragione allora?

Immaginiamo di essere 5. Il terzo a pescare pesca il suo nome. Ha immediatamente informazioni su chi NON gli farà il regalo.

Vero! I primi due hanno già pescato un altro nome e non possono farlo a lui. Non ci avevo pensato.

Pensa se il penultimo pesca il suo nome. Dovendo rimettere dentro il bigliettino, sa per certo che sarà quello dopo di lui a dovergli fare il regalo.

E infatti non è equo, c’è un altro modo?

Ripeto che non mi sembra il più grave dei problemi, ma una soluzione ci sarebbe…

E quale?

Be’, se tutti pescano e guardano i bigliettini in contemporanea nessuno ha più informazioni degli altri. E se capita che qualcuno prenda il suo nome, si ricomincia tutto da capo.

Funziona… ma no! Magari anche la seconda volta una persona estrae il suo nome, e magari anche la terza volta, e la quarta…

Fammi fare due conti. Allora, permutazioni, dismutazioni, casi possibili su favorevoli, per N grande…

Ma che dici?

Ho fatto il calcolo e, sì, hai ragione, la probabilità che qualcuno trovi il suo nome è piuttosto alta, circa il 37%, quindi può capitare di dover ripetere più volte.

E quindi che si fa?

Mmmm, non ci ho mai pensato… [riflette, cercando su Internet]… però qualcun altro l’ha fatto per te! Guarda questo video:

Non so l’inglese, spiega tu…

Allora. Per prima cosa ogni persona sceglie un numero diverso e prepara un foglio così:

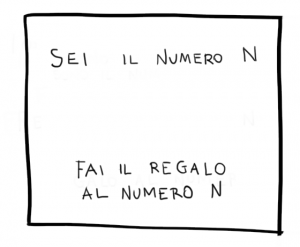
Chiaramente N è il proprio numero, giusto?

Esatto, poi i fogli si mischiano e si dispongono sul tavolo coperti.

Ok.

A questo punto, una persona li taglia tutti a metà, così:

Quindi sopra ci sono tutte le parti “Sei il numero N” e sotto tutte le parti “Regalo al numero N”. Ma dove vuoi arrivare?

Sposti di uno a destra tutti i “mezzi fogli” sopra, tranne l’ultimo che va sul primo, così:

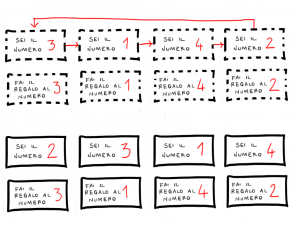
E?

E hai finito. Ognuno sceglie casualmente un foglio, parte sopra e sotto, e lo prende per sé. In questo modo ciascuno riceve un numero per se stesso e un numero diverso che indica a chi deve fare il regalo.

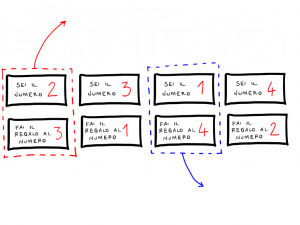
Eh ma, immaginiamo che io trovi “Sei il numero 2. Fai il regalo al numero 4.” Come faccio a sapere chi è il numero 4?

Bravo, ma basta fare una lista dei nomi. Ognuno scrive il suo nome vicino al numero che gli è capitato, oppure lo dice voce alta a tutti gli altri. Ma te sei convinto di non usare il solito metodo?

Non è così complicato questo alla fine, dai. Vabbè, ci penso domani. Piuttosto, Buon Natale!

Ah, bene. Buon Natale a te!