A ottobre a Pavia, qualcuno ha rischiato di perdere il treno per ascoltare Anna Sfard della University of Haifa, Israel. Senza nulla togliere ai numerosi accademici italiani, era lei l’ospite più atteso del XXXIII Convegno UMI – CIIM 2016, che si è tenuto a Pavia dal 7 al 9 ottobre scorso sul tema: “Criticità per l’insegnamento della matematica nella scuola di oggi”. Le slide di Anna Sfard erano in italiano (traduzione di Anna Baccaglini-Frank, le trovate qui sotto) e la sua pronuncia inglese piuttosto chiara, tuttavia abbiamo ritenuto di fare cosa utile fornire ai colleghi italiani anche la traduzione integrale della sua conferenza di Pavia. Ecco l’intervento di Anna Sfard, nella traduzione di Anna Baccaglini-Frank e Fabio Brunelli.

di Anna Sfard

1. Introduzione

Ringrazio Roberto Tortora e i colleghi dell’UMI per avermi invitato a questo interessante convegno. Cercherò di essere sintetica e di mantenermi nel tempo concessomi. Le slide sono in italiano, ma, se qualche collega ha necessità di un chiarimento, non esiti a farmi un cenno e potrò fornirgli i chiarimenti richiesti.

Come insegnanti e come ricercatori noi parliamo spesso di come le persone pensano. Invece oggi vorrei che provassimo a pensare a come parliamo noi, sia come insegnanti che come ricercatori.

I dati di fatto matematici possono essere espressi in modi diversi. Per esempio, un modo è questo: “Quando moltiplico un numero per se stesso, il valore minore che posso ottenere è zero e lo ottengo quando moltiplico zero per se stesso”; la stessa conclusione matematica la posso esprimere anche in un altro modo: “Il minimo della funzione $$f(x) = x^2$$ è $$0$$ e questo valore viene assunto per  $$x = 0$$.”

Ancora posso affermare: “Se calcolo la radice quadrata di $$x$$ ed elevo il risultato alla terza, ottengo lo stesso risultato che ottengo elevando $$x$$ alla terza e poi calcolando la radice quadrata del risultato”; lo stesso fatto matematico lo posso esprimere anche in un altro modo: “La terza potenza della radice quadrata di un numero è uguale alla radice della terza potenza dello stesso numero.”

Analogamente ai dati di fatto matematici, anche le storie riguardanti i nostri studenti di matematica possono essere raccontate in modi diversi. Per esempio, potremmo affermare: “Nella maggior parte degli esami e delle attività scolastiche X ha ottenuto punteggi sopra la media”; oppure: “X è uno studente molto abile (ha un dono)”.

Un secondo esempio: “Z ha fallito un esame dopo l’altro, nonostante abbia cercato di imparare la matematica come agli altri studenti”; oppure: “Z ha un disturbo dell’apprendimento (DSA)”.

Possiamo chiederci che cosa abbiano in comune le prime descrizioni di dati di fatto matematico o di storia umana con le seconde e anche quali siano le differenze tra le une e le altre. Mettiamo a confronto le diverse descrizioni e storie:

Riconosciamo che ogni riga presenta modi diversi di “dire una stessa cosa”. Ma le colonne presentano differenze: innanzitutto la colonna di destra è molto più sottile! Gli enunciati sono molto più brevi a destra. Ma c’è di più.

Si può notare come a sinistra le descrizioni e le storie siano narrazioni di sequenze di azioni, aventi come protagoniste le persone che le compiono. Gli enunciati della colonna di sinistra parlano di che cosa fanno le persone: per esempio, “[io] moltiplico”, “[io] posso ottenere”, “[io] ottengo”, “[io] moltiplico”, “[io] elevo”, [io] calcolo”, “X ha ottenuto”, “Z ha fallito”, … Si parla, cioè, di processi.

Invece nel modo descritto a destra compaiono oggetti e loro proprietà: nelle prime due righe compaiono gli oggetti matematici: “minimo”, “funzione”, “0”, “terza potenza”, “radice quadrata”; e nelle ultime due righe compaiono proprietà di persone: “è abile”, “ha un DSA”. A destra, dunque, si sta parlando di oggetti.

L’ “oggettificazione” è la transizione da processi a oggetti, da verbi a sostantivi. È un fatto importante? Per rispondere dobbiamo specificare in quali ambiti intendiamo parlare di oggettificazione. Parleremo dunque dell’importanza e delle conseguenze dell’oggettificazione in matematica, nel parlare sia di chi impara che dell’apprendimento.

2. Oggettificare

In particolare in questa mia relazione vorrei affrontare i seguenti 5 punti:

1. Perché ha importanza il modo in cui parliamo? (il caso dell’oggettificazione)
2. Oggettificare o non oggettificare quando si parla di chi apprende?
3. Oggettificare o non oggettificare nel fare matematica?
4. Oggettificare o non oggettificare nel fare ricerca sull’apprendimento?
5. Una lezione sull’oggettificazione per l’insegnante di matematica e il ricercatore

Ci possiamo chiedere se faccia differenza il modo in cui diciamo le cose. William Shakespeare, in “Romeo e Giulietta”, Atto II, scena II, fa dire a Giulietta: “Forse che quella che chiamiamo rosa cesserebbe di avere il suo profumo se la chiamassimo con altro nome?”

Io non sono molto d’accordo con Shakespeare. Secondo me c’è una grande differenza. Sicuramente dire di più con meno è sempre importante, a maggior ragione nell’era dell’eccessiva informazione. In matematica poi la sintesi fa addirittura parte del gioco! Ci ritorneremo a breve.

Analizziamo la differenza che fa l’oggettificazione quando parliamo di chi impara la matematica.

Come primo esempio parliamo della difficoltà nell’apprendimento come manifestazione di disturbo dell’apprendimento stesso (o disabilità). Quando si parla di disturbi o difficoltà di apprendimento come qualcosa che chi impara è, oppure ha, sono sottintesi diversi aspetti:

• la trascendenza: l’oggetto esiste nel mondo, oltre a noi;
• la depersonalizzazione: l’oggetto è dato a priori, non è un costrutto umano;
• la permanenza: come una proprietà dell’attore, non dell’azione, cioè una costante.

Dunque non spetta a noi modificare questi aspetti; il risultato è che finiamo per indirizzare gli allievi con “disabilità” su una traiettoria di vita diversa dagli altri.

Come secondo esempio pensiamo ai voti. Sono tra i più potenti “oggettificatori” (mezzi per trasformare discorsi su azioni in discorsi su proprietà dell’attore).

Invece di essere una mera valutazione di qualcosa che una persona ha fatto, diventano parte dell’identità della persona. Come tali possono più creare danni che essere utili. Su un sito online, chiamato “Attraversare tempi difficili”, ho trovato affermazioni prototipiche rispetto a ciò che si sente nella società: “I voti sono assegnati a chi apprende, nel suo interesse”, “[se prendi voti bassi] potresti sentire … dispiacere,  rabbia, intorpidimento, colpa, confusione, tristezza, malessere fisico o sconsolatezza.” Ma, mi chiedo, davvero questo è nell’interesse dello studente? Leggendo ancora si trova: “Consigli per chi prende voti bassi: ‘abbassa le tue aspettative e quelle di chi ti sta intorno”. Attenzione, non è nemmeno menzionato un apprendimento ulteriore/differente/più efficace! Teniamo conto che i voti possono arrivare a inibire l’apprendimento. Proseguendo sulla pagina si legge: “Anche se i tuoi voti non sono ciò che speravi, non significano che il tuo futuro è senza speranza, che sei un fallimento, o che non sarai capace di compiere cose grandiose”. Non ci sarebbe bisogno di questa affermazione se i voti non facessero da biglietto da visita per il futuro di una persona. Purtroppo molti voti brutti saranno proprio un biglietto da visita. Dunque i voti non solo riflettono la realtà, ma arrivano a modellarla e non sempre nel modo migliore.

Possiamo quindi affermare che l’oggettificazione è sia vantaggiosa che pericolosa. Quando parliamo di chi apprende l’oggettificazione è pericolosa: è meglio cercare di usare verbi che riguardano il fare, invece che sostantivi riguardanti ciò che uno è, oppure ha. Ripensando alle storie di studenti di matematica, ritengo che sia meglio raccontare la storia come nella colonna di sinistra, e cioè dire, per esempio: “Z ha fallito un esame dopo l’altro, nonostante abbia cercato di imparare la matematica come gli altri studenti”, piuttosto che: “Z ha un DSA”.

Ci si può chiedere allora se sia davvero necessario togliere gli oggetti dal discorso e, se anche lo fosse, se sarebbe davvero possibile farlo. La risposta ad entrambe le domande è affermativa: come scrive Perry Link, in cinese le persone usano solo verbi per dire quello che in inglese (e in italiano) si dice con sostantivi. Nelle lingue occidentali a volte usiamo sostantivi per concepire cose anche quando non ne abbiamo proprio bisogno (Perry Link, 2013). In uno studio di Dong-Joong Kim (Dong-Joong, Ferrini-Mundy & Sfard, 2012) si vede come gli studenti che parlano coreano hanno difficoltà a usare il sostantivo “infinito”, anche se usano l’aggettivo “infinito” e l’avverbio “infinitamente”.

Ma com’è che questi, che sembrano solamente giochi di parole, ci possono aiutare? Eliminando questi oggetti dal nostro parlare, essi spariranno dal mondo? Per esempio, eliminare la parola “discalculia” farà sì che il mio studente guarisca da questa disabilità? Se ci pensiamo, alcuni di questi fatti (oggetti), inclusa la discalculia, non esistono a meno che ci si metta a parlarne. Più precisamente, molti dei fatti (oggetti) di cui parliamo sono costrutti discorsivi: sono il nostro modo di parlare di fenomeni.

Troviamo oggetti ovunque nella ricerca. Pensando alle scienze naturali e alla matematica ci sono moltissimi oggetti, come ad esempio “forza”, “energia”, “numero”, “funzione”, “insieme”. Nelle scienze umane invece troviamo oggetti come “conoscenza”, “concetto”, “significato”, “credenza”, “attitudine”, “valore”, “personalità”, “carattere”, “identità”, “disabilità”, “dono”, “discalculia”, “ego”, “superego”… È difficile immaginare che potremmo parlare dei fenomeni (processi), senza riferirci a questi oggetti, ma è possibile farlo!

Prima di proseguire vorrei fare una dichiarazione di limitazione di responsabilità: quando chiedo di evitare la parola “discalculia”, non sto negando l’esistenza dei fenomeni che hanno dato origine alla parola. Questa dichiarazione è in linea con quanto affermato da Kuhn (1962).

In definitiva sta a noi decidere se oggettificare (parlare per sostantivi, anziché per verbi) o meno.

Abbiamo discusso finora l’oggettificare quando si parla di chi apprende. Ora chiediamoci se valga la pena o meno di oggettificare nel fare matematica. In matematica non si ha scelta: bisogna oggettificare, perché la matematica semplicemente non esiste senza oggettificazione! Che cos’è la matematica? Come la biologia è un’attività in cui si narrano storie utili sugli essere viventi (piante, animali), e la fisica è un’attività in cui si narrano storie utili  sulle cose naturali (corpi in movimento, luce, ecc.), anche la matematica è un’attività in cui si narrano storie utili di oggetti matematici (numeri, insiemi, funzioni, figure geometriche). Ma a differenza della biologia o della fisica, in matematica tutti questi oggetti sono creati nell’atto della narrazione stessa! Nonostante questo, le storie matematiche sono importanti nel mondo reale. In che modo?

Vediamo come e perché nascono gli oggetti matematici. Prendiamo come esempio il numero.

Guardate le quattro immagini qui sotto. Secondo voi rappresentano la stessa persona?

Come si può giustificare l’affermazione che effettivamente le immagini rappresentano la stessa persona? È difficile dirlo, eppure siamo tutti d’accordo che lo stesso oggetto (una persona) è raffigurato in tutte queste immagini.

Chiediamoci, ancora, che cosa significa “lo stesso” in queste altre cinque immagini. È mostrato lo stesso oggetto in tutte queste immagini? Quale oggetto?

Rispondete “cinque”? Ma dov’è il numero cinque? La verità è che l’unica caratteristica percettibilmente accessibile in tutte queste figure è che, se contiamo i loro elementi, finiamo con la parola “cinque”. Dunque è lo stesso processo che è coinvolto in tutte le immagini.

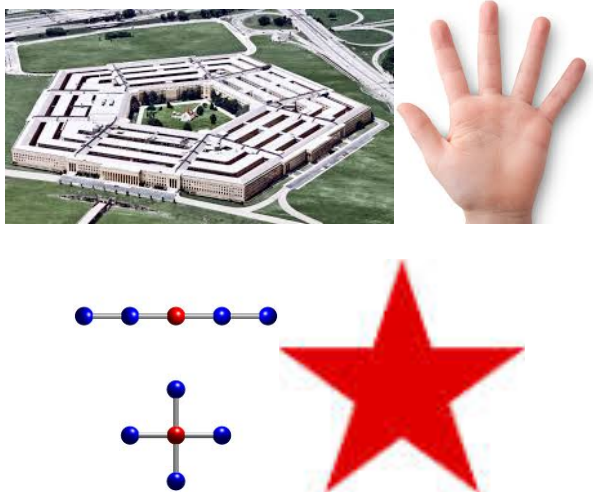
In conclusione, il numero è solo una metafora; è un’oggettificazione del processo di conteggio. L’oggettificazione consiste nell’usare un simbolo (parola), come se significasse un oggetto del mondo, che esiste indipendentemente da noi; poi diciamo che il simbolo (parola) rappresenta l’oggetto. L’oggettificazione può essere vista come un tipo speciale di metafora ed è il processo discorsivo che ci fa utilizzare parole e simboli matematici come se significassero oggetti indipendenti dal discorso stesso. Comprende: la reificazione (lo scambio di verbi con sostantivi) e l’alienazione (la rimozione del soggetto umano).

Perché oggettifichiamo il numero? Proviamo a immaginare di non poter usare più le parole “numero uno”, “numero due”, “numero tre”… tranne che nei processi di conteggio. Allora come si potrebbe esprimere la seguente uguaglianza 3 + 4 = 7? Per esempio così: “Se ho un insieme tale che tutte le volte che conto i suoi elementi arrivo alla parola “tre” e mi fermo, e ho un secondo insieme tale che tutte le volte che conto i suoi elementi arrivo alla parola “quattro” e mi fermo, e se metto insieme gli elementi dei due insiemi, allora se conto gli elementi del nuovo insieme, arrivo sempre alla parola “sette” e mi fermo.” Certo sarebbe una fatica enorme se dovessimo continuare a sviluppare la matematica basandoci sulla descrizione a destra! Con l’idea di oggettificazione si possono capire meglio alcuni dei motivi per cui la matematica risulta così difficile per così tanti studenti. In particolare, se i numeri (insiemi, funzioni, ecc.) sono processi diventati oggetti, e non si è consapevoli del processo secondo cui questo è avvenuto, è come se non potessimo distinguere tra una ricetta e una torta, che invece riconosciamo essere ben differenti!

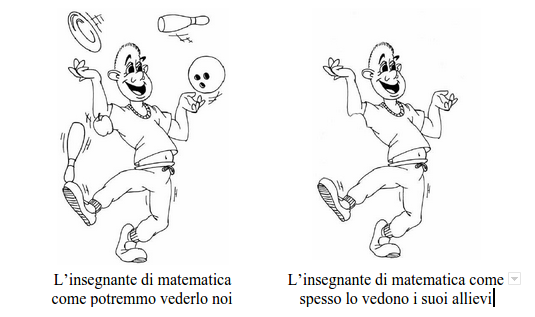
Agli occhi dei suoi studenti spesso l’insegnante appare come un giocoliere di cui essi non riescono a vedere gli oggetti che lancia in aria.

Passiamo ora alla penultima parte di questa presentazione: discutiamo sull’utilità di oggettificare o meno nel fare ricerca sull’apprendimento. Che differenza fa parlare “in termini di oggetti” per gli studiosi dell’apprendimento, e in particolare per coloro che fanno ricerca sull’apprendimento della matematica? Pensiamo a come due ricercatori possono raccontare i propri studi.

Un primo ricercatore dice: “I bambini sotto i cinque anni spesso non si accorgono che è l’ultima parola nel processo di conteggio degli elementi di un insieme che definisce il numero di elementi dell’insieme.” Un secondo ricercatore dice: “I bambini sotto i cinque anni spesso non si accorgono che i conteggi ripetuti degli elementi dello stesso insieme devono finire tutti con la stessa parola-numero.” Questi due ricercatori stanno parlando della stessa cosa? E di che cosa allora? Sembrerebbe che stiano parlando di ciò che alcuni ricercatori hanno nominato il “principio di cardinalità” (Gallistel e Gelman, 1991). Ma ci sono varie differenze: il primo ricercatore parla della proprietà di un oggetto (“numero”), mentre il secondo parla di una proprietà di un processo discorsivo (il “conteggio ripetuto” che finisce con la stessa “parola-numero”).

Analogamente, i due ricercatori potrebbero così raccontare. Il primo: “I bambini sotto i cinque anni spesso non si accorgono che è la balena il più grande mammifero”; e il secondo: “I bambini sotto i cinque anni spesso non si accorgono che le espressioni linguistiche “balena” e “mammifero più grande” possono essere scambiate tra loro.” Il primo ricercatore parla delle proprietà di un oggetto (balena), mentre il secondo parla di proprietà del processo discorsivo (il fatto che alcune parole possano essere scambiate tra loro).

Parlare di oggetti non è lo stesso che parlare dei loro nomi. Per esempio, se si dice: “I bambini sotto i cinque anni non si accorgono che la balena è il più grande mammifero” si sta assumendo che il bambino possa aver avuto esperienza diretta di balene prima di conoscere loro proprietà. Se sostituiamo “balena” con “numero” l’assunzione diventa: “Il bambino può aver avuto esperienza diretta del numero prima di conoscere le sue proprietà”, che è palesemente assurdo – è una metafora di oggetto portato a conseguenze troppo estreme.

Dunque il primo testo implica che nella vita di un bambino i numeri esistono prima del discorso sui numeri. Il secondo testo, invece, è in linea con l’affermazione che i numeri nascono dal discorso. Inoltre, nel primo testo imparare la matematica significa raccontare storie sugli oggetti indipendentemente dalle storie stesse e da chi le narra; mentre nel secondo, imparare la matematica significa creare gli oggetti sui quali le storie matematiche sono raccontate. Ancora, dal primo testo sembra che il bambino impari dal mondo stesso, mentre dal secondo sembra che il bambino impari innanzitutto dalle persone che ha intorno. Questa differenza, in particolare, può avere implicazioni profonde nella nostra comprensione dell’apprendimento e della pratica didattica.

3. Conclusioni

Per finire vorrei impartire una piccola lezione sull’oggettificazione per l’insegnante di matematica e per il ricercatore. Da quanto detto sopra è evidente che dobbiamo fare attenzione a come parliamo. Questo è vero per tutti coloro che si occupano di matematica: matematici, studenti di matematica, insegnanti di matematica e anche ricercatori. È vero che in matematica dobbiamo imparare a oggettificare: lo devono fare sia il matematico che inventa nuova matematica, che lo studente che cerca di partecipare al discorso matematico già esistente. Noi come insegnanti dobbiamo aiutare chi impara a oggettificare ed evitare oggettificazioni quando parliamo di chi impara.

E che cosa dire ai ricercatori che si accingono a studiare processi di apprendimento della matematica? Il ricercatore che chiede: “Che cosa sanno i bambini dei numeri?” è un po’ come uno storico che chiede: “Che cosa sapevano fare le persone nel Medioevo con le automobili?”. Il resoconto dello storico potrebbe essere: “Le persone non sapevano che le auto possono correre persino a 200 km/h; esse non usavano le automobili quando sarebbe stato utile.” Analogamente, il resoconto del ricercatore che si pone una domanda come quella sopra, potrebbe essere: “I bambini non sapevano che i numeri possono diventare infinitamente grandi; loro non usavano numeri quando sarebbe stato utile.” In entrambi i resoconti compaiono i verbi “non sapevano” e “non usavano”. Questo crea discorsi su deficit in cui il ricercatore parla di ciò che i bambini non fanno e ignora ciò che davvero fanno. Ma così come le persone nel Medioevo viaggiavano anche se non c’erano le automobili, così anche i bambini fanno cose senza i numeri che poi faranno con i numeri. Per esempio, i bambini prendono decisioni, alcune delle quali sono di tipo quantitativo. Ed è proprio dall’attività di scelta che lo studio dello sviluppo del pensiero numerico dovrebbe iniziare e dovrebbe proseguire come attenta continuazione dello sviluppo di routine delle loro attività di scelta. Come ricercatori, dobbiamo proprio cambiare prospettiva, passando da interni ad esterni al nostro discorso matematico.

Vorrei concludere con un’esortazione e una domanda: “Pensa a come parli! Che ne pensi di parlarne ora?”

Grazie!

Le Slide della presentazione di Anna Sfard, tradotte da Anna Baccaglini Frank, per gentile concessione dell’autrice

[google-drive-embed url=”https://docs.google.com/presentation/d/1G0Y3c0nyQvcziA3CL-ovAhb83LUh41HJ9SvPaEE0yTA/preview” title=”how we talk – Pavia – 9 Oct_v3_ita.pptx” icon=”https://ssl.gstatic.com/docs/doclist/images/icon_11_presentation_list.png” width=”100%” height=”400″ style=”embed”]

Riferimenti bibliografici

Dong-Joong, K., Ferrini-Mundy, J., & Sfard, A. (2012). International Journal of Educational Research. International Journal of Educational Research, 51-52, 86–108.

Gallistel, C.R. & Gelman, R. (1992). Preverbal and verbal counting and 
computation. Cognition 44, 43-74.

Kuhn, T. S. (1962). The Structure of Scientific Revolutions. International Encyclopedia od Unified Science.

Link, P. (2013). An Anatomy of Chinese Rhythm, Metaphor, Politics. President and Fellows of Harvard College.

Sfard, A. (2009). Psicologia del pensiero matematico. Trento: Erickson.

Shakespeare, W. (1597). Romeo and Juliet.