Continua la rubrica “Uno sguardo oltre la superficie“, a cura di Giuseppe Tinaglia. Uno spazio dove si osserva la geometria che ci circonda, ma anche oltre.

Sabato scorso la mia amica Barbara mi ha invitato a cena a casa sua. Dopo cena ha voluto farmi vedere il bagno: lo sta sistemando. Mi domanda “Tu come piastrelleresti questa parete? Qual è il modo migliore?” La domanda mi ha subito gettato nel panico. Cosa? In che senso migliore? A cosa si riferisce? Al colore? Argh! Barbara mi conosce e vedendo l’esitazione trasudare dal mio volto, mi ha subito soccorso. “Lascia perdere, non ti preoccupare. Chiedo consiglio a Giovanni.” Tornando a casa però, mi è tornata in mente la domanda di Barbara. Da lì è nato questo articolo. Si perché, con la sua domanda, Barbara ha in un certo modo illuminato uno dei tanti problemi irrisolti della geometria: la congettura di Kelvin. Si, si, Kelvin, quello della temperatura.

Mi spiego. Come al solito in matematica, ma anche nella vita, capire la natura del problema rappresenta mezza soluzione. E,  come al solito, per capire meglio il problema bisogna capire bene di che cosa si stia parlando, dare le appropriate definizioni, senza lasciare troppe ambiguità. Per questo motivo, prima di affrontare la congettura di Kelvin, voglio parlare di un problema di geometria piana che ha a che fare con le cosiddette tassellature.

Cosa vuol dire tassellare il piano?

Tassellare il piano vuol dire ricoprire il piano (e mi riferisco al piano infinito!) con una figura geometrica ripetuta all’infinito, senza spazi vuoti e senza sovrapposizioni. Proprio come le piastrelle del bagno o del pavimento, se la parete si estendesse all’infinito. Per esempio, una tassellatura del piano si può fare con un quadrato, un triangolo equilatero, un esagono regolare

o figure molto più fantasiose come nei fantastici mosaici della Alhambra, a Granada in Spagna

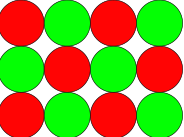
Ricoprire il piano di dischi invece, NON è una tassellatura, perché rimangono degli spazi vuoti.

 

Dopo questo preambolo, possiamo finalmente trasformare la domanda di Barbara in un problema matematico chiaro, e sufficientemente privo di ambiguità. Il problema è questo:

Qual è la figura geometrica capace di tassellare il piano e tale che il rapporto \(\frac{Area}{Perimetro^2}\) sia il più grande possibile? Per esempio, se usassimo un quadrato di lato 1 allora l’area sarebbe 1, il perimetro 4, e quindi il rapporto di cui sopra \(\frac{1}{16}.\) Per prima cosa notate che il rapporto non dipende dalla lunghezza del lato. Se non ci credete, fate la prova! Cosa ha a che fare questa domanda con le piastrelle? Beh, una piastrella è ovviamente una figura geometrica con una certa area e un certo perimetro! Inoltre, scelte due piastrelle differenti ma con lo stesso perimetro, chiamiamole A e B, notate che se il sopradetto rapporto è più grande per la piastrella A, allora l’area occupata dalla piastrella A è più grande dell’area occupata dalla piastrella B. Cosa vuol dire? Vuol dire che, in un certo senso, usando la piastrella A si ricopre più area con meno piastrelle. Si riduce lo sfrido!

Torniamo agli esempi di tassellature. Se usassimo un quadrato di lato 1 allora il rapporto è \(\frac{1}{16}.\) Se usassimo un triangolo equilatero di lato 1, allora il rapporto sarebbe è \(\frac{\sqrt{3}}{36}\). Se infine usassimo un esagono regolare, allora il rapporto sarebbe è \(\frac{\sqrt{3}}{24}\). Se ho fatto bene i conti, \(\frac{\sqrt{3}}{36}<\frac{1}{16}<\frac{\sqrt{3}}{24}\). Quindi, per questo problema, tra una piastrella quadrata, una triangolare e una esagonale, il rapporto più grande si ha con la piastrella esagonale che quindi è la piastrella “migliore”!

Ricordatevi che stiamo immaginando di piastrellare una parete infinita.

Ma fra tutte le possibili piastrelle qual è il migliore rapporto? Non è che possiamo metterci a calcolare un numero infinito di aree e di perimetri! Si dà caso che si possa dimostrare che la piastrella esagonale le batte tutte! Qualsiasi altra forma geometrica, darebbe un rapporto minore di \(\frac{\sqrt{3}}{4}\). La piastrella esagonale è quella che minimizza lo sfrido! Adesso telefono a Barbara. Ma prima, la congettura di Kelvin.

La congettura di Kelvin ha a che fare con un problema esattamente analogo a quello precedente delle tassellature, ma nello spazio anziché nel piano. Invece di considerare il rapporto \(\frac{Area}{Perimetro^2}\), si considera il  rapporto \(\frac{Volume^2}{Area^3}\).  Il problema è questo: Qual è la figura geometrica 3-dimensionale che permette di ricoprire lo spazio e tale che il rapporto \(\frac{Volume^2}{Area^3}\)  sia il più grande possibile?

In maniera analoga alle tassellature, si può ricoprire lo spazio di cubi, tetraedri regolari, parallelepipedi. In più, un bellissimo esempio di ricoprimento dello spazio viene costruito in natura dalle api, ovvero l’alveare. Ci sono poi le spugne che sono ricoprimenti dello spazio, ma non necessariamente regolari. Sull’utilità di trovare la figura geometrica 3-dimensionale per cui il sopraddetto rapporto sia il maggiore possibile,  si possono fare considerazioni analoghe a quelle fatte per le tassellature.

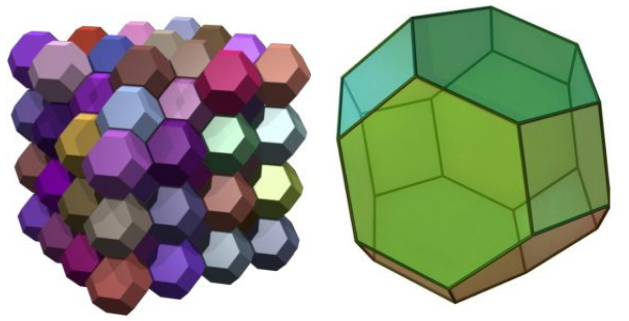
La congettura di Kelvin, datata 1887, afferma che la soluzione a questo problema è una figura geometrica molto simile al favo di un alveare, molto simile a quello che si chiama un ottaedro troncato.

Un momento! Fermatevi! Prima che andiate a cercare carta e penna per dimostrare la congettura di Kelvin, vi devo dire una cosa. La congettura è falsa. Ebbene si, nel 1993, quindi dopo più di cento anni, Weaire e Phelan ^{[1 ]}Weaire, D.; Phelan, R. (1994), A counter-example to Kelvin’s conjecture on minimal surfaces, Phil. Mag. Lett., 69. sono riusciti a trovare una struttura che, a parità di volume, riduce l’area del tre per cento.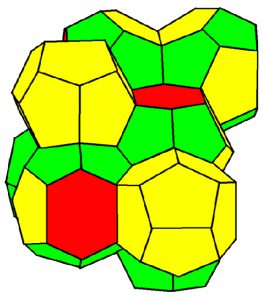 Questa struttura è stata appropriatamente chiamata la struttura di Wearie e Phelan e, nota curiosa, è servita da ispirazione nella costruzione del centro acquatico di Pechino, costruito e utilizzato per le olimpiadi del 2008.

Sarà la struttura di Weaire e Phelan la struttura migliore? Chissà? Comunque sia, va dato atto alle api di avere fatto un ottimo lavoro!

Un’ultima cosa a riguardo delle tassellature. Si possono tassellare anche superfici diverse dal piano e dove la geometria non è necessariamente Euclidea. Per esempio, alcuni bellissimi quadri di Escher rappresentano tassellature del piano iperbolico. Ma questa è un’altra storia.

 

 

Giuseppe Tinaglia, King’s College, London

https://nms.kcl.ac.uk/giuseppe.tinaglia/