di Davide Palmigiani

“La geometria frattale cambierà a fondo la vostra visione delle cose. Continuare a leggere è pericoloso. Si rischia di smarrire definitivamente l’immagine inoffensiva che si ha di nuvole, boschi, galassie, foglie, piume, fiori, rocce, montagne e di molte altre cose. Mai più tornerete a recuperare le interpretazioni di tutti i questi oggetti che finora vi erano familiari.”

Così Micheal Barnsley introduce il suo Fractals Everywhere, testo su un piatto ghiotto di Matematica Umida (qui, qui e qui le altre puntate). I frattali sono ovunque e, per tenerlo bene in mente, si partecipa alla lettura di questo articolo attivamente: ritaglia una striscia di carta abbastanza lunga; ad ogni iterazione dell’articolo dovrai piegare a metà il foglio, sempre nella stessa direzione, un numero di volte pari all’iterazione che stai leggendo, e poi riaprirlo in modo che tutte le pieghe formino angoli retti, a formare una figura particolare.

Iterazioni? Nient’altro che un modo originale per chiamare i capitoli (preso in prestito da Jurassic Park, il libro, di Michael Crichton) e un modo per scandire il tempo di questo articolo un po’ lungo (che inizialmente sarebbe dovuto consistere in due puntate, da cui il doppio titolo).

Prima Iterazione

“Le configurazioni iniziali della curva frattale offrono scarse indicazioni sulla struttura matematica sottostante.”

1. Tra due punti qualsiasi è possibile tracciare una e una sola retta

2. Si può prolungare un segmento oltre i due punti indefinitamente

3. …

4. …

5. Per un punto passa una e una sola parallela ad una retta data Con questi assiomi si costruisce la geometria euclidea e nelle forme di questa si riconoscono figure naturali: sfere, cubi, esagoni, rette. Platone pensava di poter spiegare la Natura con le forme dei suoi cinque poliedri regolari,

ma forme è un concetto più astratto e profondo; non solo cubi e prismi, non solo Natura visibile, ma la storia della scienza: Newton mostrò che nello spazio ci si muove con ellissi, figure semplici ed eleganti; scienze più moderne parlano di onde, seni e coseni, radio, energia elettrica e magnetismo; teorie ancor più moderne evolvono il concetto in onde di probabilità, equazione di Schroedinger, meccanica quantistica. Modelli e parole sempre più difficili, ma tutte forme matematiche belle, lisce e levigate. E se così non sono, lo sono almeno in buona approssimazione. In che senso? La Natura non è che sia proprio un solido platonico perfetto, però più o meno; non è che la Terra sia veramente sferica, ma più o meno; non è che la Francia sia esagonale, ma in prima approssimazione; non è che un pino sia proprio un cono, ma se scientificamente è una conifera, un motivo ci sarà! Mmmm, però, a pensarci meglio…

Seconda Iterazione

“In configurazioni successive della curva frattale possono verificarsi improvvisi mutamenti”

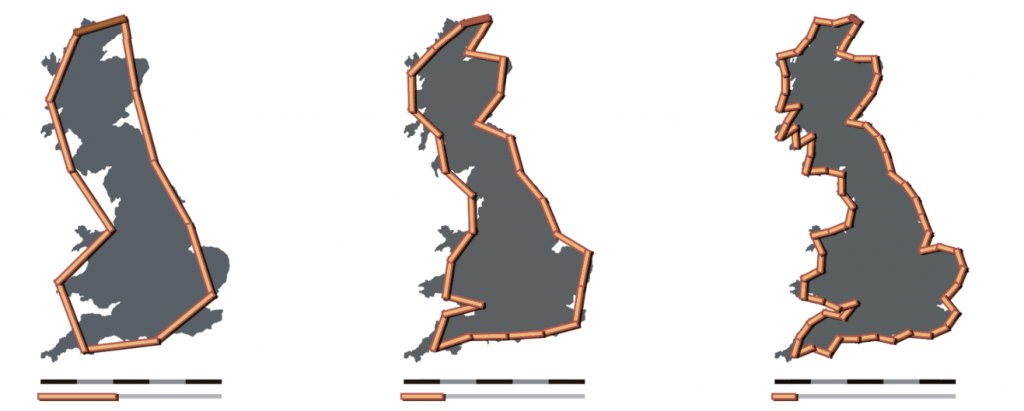
…a pensarci meglio di forme naturali matematiche precise, lisce, non frastagliate, non che ce ne siano poi così tante. Se pensiamo ad un cubo, una sfera, una piramide, vengono in mente case, palloni, monumenti egizi… ma questi non contano! Sono così perché noi li abbiamo voluti così, abbiamo pensato ad un’immagine astratta e l’abbiamo riprodotta. Per la Natura vale lo stesso o siamo solo noi che a volte cerchiamo di ingabbiarla in “precise” forme euclidee, ignorando le imperfezioni che, forse, sono ciò che più conta? Che poi ignorare le forme frastagliate, anche solo come approssimazione, in alcuni casi porta proprio a dei problemi. Nella prima metà del 900, tal Lewis Fry Richardson, uno scienziato e pacifista inglese, studiava la relazione tra probabilità che due Paesi entrino in guerra e la lunghezza dei confini geografici comuni; si accorse di due fatti particolari. Primo, le misure fatte da Stati diversi non coincidevano: la Spagna diceva che la sua frontiera con il Portogallo fosse di 987 km, per il Portogallo erano invece 1214. Per l’Olanda la frontiera con il Belgio era di 380 km, per quest’ultimo 449. Dove nascono le disparità? Diversi Paesi utilizzano diverse unità di misura e quindi, misurando in maniera approssimata, ottengono valori differenti… Se provate a misurare una circonferenza usando una barretta rigida otterrete la lunghezza di una poligonale, una spezzata, perché la vostra unità di misura non riesce a tener conto delle convessità minori della sua lunghezza. Prendendo una barretta più corta, andrà sicuramente meglio; ovviamente, più è piccola l’unità, più sarà precisa la misura. Fatto è che, diminuendo sempre più, si otterrà proprio la lunghezza esatta (6.28 moltiplicato il raggio iniziale). Però Richardson si accorse di un altro fatto, molto più particolare: nel caso dei confini geografici l’ultima frase non vale!

Diminuendo l’unità di misura, la lunghezza dei confini continua ad aumentare seguendo tutte le frastagliature, ad aumentare, aumentare… rendendo di fatto la costa della Gran Bretagna lunga infinito! Non è molto chiaro vero? Normale, ma per il momento sia invece chiaro che…

Terza Iterazione

“Ridisegnando la curva frattale i dettagli emergono più chiaramente”

  …sia chiaro che una buona descrizione della Natura non può ignorare tutte le rugosità e le imprecisioni che rendono ciò che ci circonda Vero. La Natura ha scelto di plasmarsi nelle forme frastagliate dei frattali!

Quarta Iterazione

“Inevitabilmente, le instabilità nascoste cominciano ad apparire”

I frattali sono oggetti con proprietà molto particolari ed è facile riconoscerne in Natura perché La Natura seleziona forme matematiche per ottenere vantaggio evolutivo e di vantaggi ce ne sono, eccome. Prendiamo il Fiocco di Neve di Koch.

Le immagini che si trovano sono sempre delle approssimazioni di ciò che si ottiene da questo algoritmo: Si parte da un triangolo equilatero; si divide ogni lato in tre segmenti di uguale lunghezza; si cancella il segmento centrale e si sostituisce con i due lati del triangolo equilatero di cui lui sarebbe la base; si ripete dall’inizio, utilizzando come figura iniziale quella che si è ottenuta. Ripetendo il meccanismo infinite volte (in Natura “infinite volte” si traduce in “molte volte”)… ecco il Fiocco di Neve.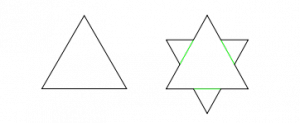

Ragioniamo sul perimetro. Ogni lato viene diviso in tre parti, poi se ne ottengono quattro, ognuna lunga un terzo del lato iniziale; questo vuol dire che, ad ogni iterazione, il perimetro cresce e diventa i 4/3 del precedente. Se inizialmente è 3, diventa 4, poi 5.33, poi 7.11, 9.48, 12.64…infinito! E l’area? Come si può vedere dai disegni, tutta la figura completa entra nel foglio (virtuale, a meno di stampa), quindi la sua area è più piccola di quella di quest’ultimo, che non è infinita! Il calcolo preciso (che si può trovare qui) porta a concludere che l’area totale è gli 8/5 di quella iniziale; partendo da un triangolo di area 1 metro quadro, il fiocco di neve ha area 1.6 metri quadri. Folle! Perimetro infinito e area finita! Che vantaggio evolutivo può dare questa struttura? Chiedetelo al vostro intestino. Questo squilibrio tra perimetro ed area (in tre dimensioni tra superficie esterna e volume) è la perfezione per quel che riguarda assorbimento di sostanze nutritive. L’intestino umano è un tubo arrotolato con lo scopo di digerire ed assorbire sostanze nutritive, ripiegato così tante volte su se stesso che, seppur contenuto in un volume modesto, raggiunge gli 8 metri di lunghezza. La parete interna dell’intestino è piena di estroflessioni, chiamate villi, che consentono di aumentare la superficie dell’organo ed avere una maggiore area assorbente, ma non basta! La membrana delle cellule che formano i villi presenta ulteriori estroflessioni, dette microvilli, sottilissime, alte circa un milionesimo di metro (quindi osservabili in maniera nitida esclusivamente con microscopio elettronico). La struttura frattale è evidente.

Spostandoci solo di qualche decina di centimetri troviamo un altro frattale:

La capacità respiratoria di un animale è direttamente legata alla superficie dei suoi polmoni, che sono formati da strutture sempre più piccole, tanto che, ben aperti e dispiegati, potrebbero riempire un campo da tennis. Ma…

Quinta Iterazione

“Ora le imperfezioni del sistema diventeranno serie”

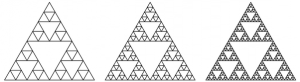
…ma sappiate che l’Evoluzione non ha sfruttato i frattali solo per questo. Una delle proprietà più caratteristiche, se non La più caratteristica, è quella che prende il nome di Autosimilarità, il fatto di somigliare a copie più piccole di se stessi; è così insita nel mondo naturale che non ce ne accorgiamo neanche: un arco di cerchio non è un cerchio, un lato di un triangolo non è triangolare, alberi, nubi, montagne invece sì che sono autosimili!. Quando facciamo un presepe, si può prendere un sasso per una montagna, un ramoscello per un albero, un pezzo di nuvola (ma va bene anche l’ovatta) per le nuvole, ma non un mattone per una casa. L’autosimilarità è nella definizione stessa di frattale, basta guardare la costruzione del triangolo di Sierpinski: si parte da una figura qualsiasi e si trasforma in qualcosa che è fatto più o meno da copie ridotte della prima, e si ripete…

Gli esempi più vistosi di autosimilarità naturale sono forse questi:

 Il broccolo romanesco ci urla in faccia “io sono un frattale!” almeno quanto questa felce

Barnsley (quello dell’introduzione) mostrò che tramite tre trasformazioni matematiche (vedi qui per informazioni più dettagliate) ripetute all’infinito si ottiene questo:

Simulazioni al computer di oggetti naturali, come foglie, tramite questo processo iterativo generano immagini praticamente indistinguibili dalla realtà…che l’Evoluzione abbia scelto proprio questo meccanismo per generare le sue forme? Se sì, perché? Risposta semplice e geniale. I codici genetici di piante ed altri esseri viventi si basano su quello che si può chiamare “principio di minima azione”, cioè la ricerca di massima economia quando si generano le istruzioni per la crescita. Per questo motivo è così diffusa l’autosomiglianza nella loro morfogenesi e la maggior parte hanno una struttura frattale. Perché inserire nel DNA una quantità enorme di informazioni per descrivere nel dettaglio l’organismo, durante lo sviluppo, quando basta dare come istruzione solamente quella di ripetere in continuazione un’unica regola di trasformazione?

Sesta Iterazione

“Il recupero del sistema potrebbe rivelarsi impossibile”

Autosimilarità, procedimento iterativo, perimetri infiniti e aree finite, il pezzo di carta che tenete in mano e che ormai non dovreste più riuscire a piegare, si possono comprendere ancora più a fondo una volta dato senso all’espressione

“I frattali sono oggetti a dimensione non intera”

Il concetto di dimensione è piuttosto familiare: un segmento o una curva hanno dimensione 1, un quadrato 2, un cubo 3. Se proviamo però ad applicare questo concetto ai frattali otteniamo numeri non interi: il bordo del fiocco di neve di Koch ha dimensione 1.262, il triangolo di Sierpinski 1.585. La dimensione ci dà un’idea di quanto il frattale sia frastagliato e quanto somigli ad una curva piuttosto che ad una figura piana, o un solido. La superficie del cavolfiore, nella quale ogni ramo ha 13 rametti 3 volte più piccoli, non ha dimensione 2 (come le superfici “normali”) ma 2.33, più vicina ad un solido. Gli alveoli polmonari formano una superficie frattale di 2.97, praticamente 3! E il pezzo di carta che avete in mano? Quel frattale si chiama curva (dimensione 1) del drago e matematicamente si ottiene comprimendo di un fattore radice di 2 la curva iniziale e creando due copie ruotate di 45 e 135 gradi (qui una spiegazione più precisa)

La sua dimensione frattale è 2! Questo vuol dire che è così fitta che all’infinito smette di essere una curva e diventa un piano! È un peccato che più di 6,7 volte a mano non di possa piegare, vero?

Settima Iterazione

“Le matematiche richiederanno sempre maggior coraggio per affrontare le loro implicazioni”

Bibliografia

Un nuovo modo di vedere il mondo – I frattali – Il Mondo Matematico

I frattali a fumetti – N. Lesmoir-Gordon, W. Rood, R. Edney

La piccola bottega delle curiosità matematiche del professor Stewart – Ian Stewart

Decisamente più tosto (due link che si trovano nell’articolo possono essere presi come riassunto): Teorema delle contrazioni e sistemi di funzioni iterate – Luigi Orsina

Esistono frattali di tipo diverso da quelli di cui abbiamo parlato, ma comunque molto famosi:

L’insieme di Mandelbrot – il frattale PIÙ famoso (video)

Attrattore di Lorenz – ovvero “Perché il meteo non ci prende mai”

Wikipedia contiene pagine interessanti a riguardo