Una mini-serie a cura di Gabriele Belegni, dove esploreremo i concetti principali di una delle branche più affascinanti della matematica: la topologia. Cercheremo di scoprire le motivazioni e le idee che hanno spinto ad introdurre certi concetti concentrandoci sull’aspetto intuitivo piuttosto che su quello formale. In questa puntata conclusiva parleremo di alcune delle innumerevoli applicazioni della topologia. Trovate tutte le puntate su questa pagina.

Abbiamo parlato di topologia per 7 puntate, esplorandone gli aspetti principali e le idee fondamentali, ma immagino che molti di voi avranno avuto in testa più volte la stessa domanda: “Ok, ma a che serve tutta questa roba?”. A tantissime cose! Ma veramente tante, raccontarvi tutte le possibili applicazioni della topologia è improponibile, sono semplicemente troppe, non a caso ci sono libri interamente dedicati ad esse, ma penso che la nostra chiacchierata sulla topologia non può concludersi senza aver parlato almeno di alcune di esse.

La prima cosa che voglio mostrarvi è la grande utilità del concetto di omologia (se non lo avete mai sentito, ne abbiamo parlato nella puntata 6!), che pure sembra essere uno dei più astratti, nell’analisi dei dati. Raccogliere dati significa misurare vari parametri di un certo campione di riferimento, e l’insieme dei dati raccolti formerà una cosiddetta nuvola di punti. Mi spiego: se misuriamo solo 2 parametri, ad esempio altezza e peso di una popolazione, allora possiamo rappresentare ogni dato (cioè ogni coppia altezza-peso) come un punto nel piano \(\mathbb{R}^2\), insomma usando 2 coordinate, una corrispondente al peso e una all’altezza. Misurando questi parametri su varie persone, cioè raccogliendo vari dati, otterremo una nuvola di punti nel piano come quella che vedete in figura 1. In generale la forma della nuvola di punti può darci informazioni molto interessanti sul comportamento del fenomeno che stiamo studiando, ad esempio in figura 1 la nuvola di punti ottenuta mostra che c’è un legame pressoché lineare tra i due parametri, nel senso che aumentano insieme e con la stessa “velocità”.

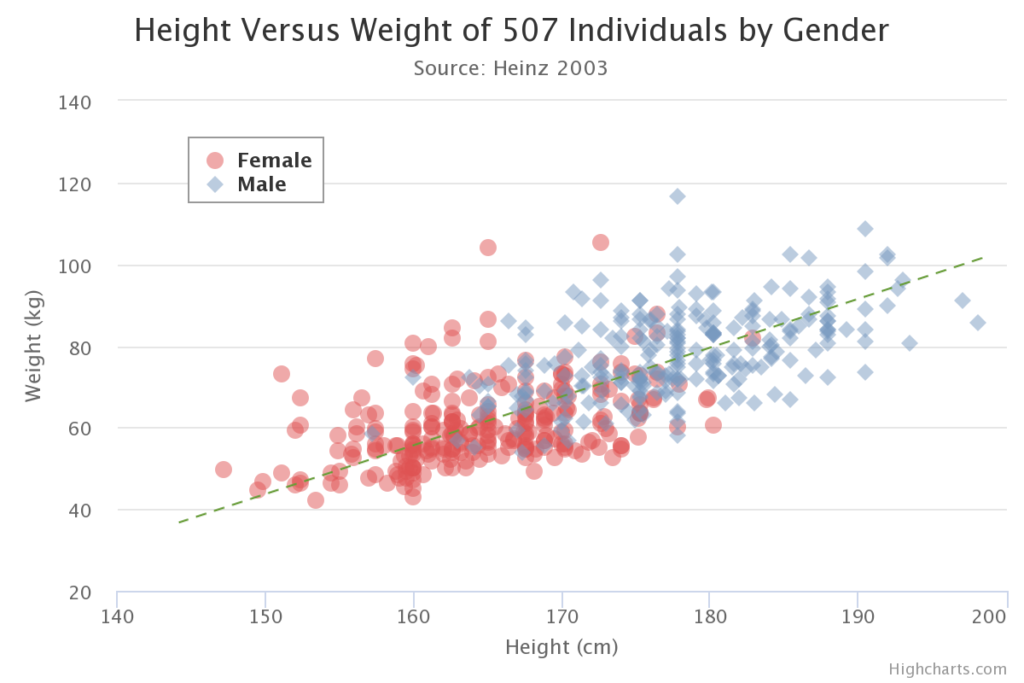Figura 1: Dati altezza-peso raccolti su un campione di 507 individui. Da notare il legame lineare tra le due quantità. [1]

Finché si tratta di questo semplice esperimento non c’è bisogno di chissà quale matematica, insomma sappiamo già benissimo che in genere più si è alti e più si pesa, ma nella maggior parte delle situazioni i dati che raccogliamo dipendono da molti più di due parametri e quindi la loro rappresentazione e il loro studio non sarà più così semplice. Non saranno più dei punti nel piano ma dei punti in uno spazio a più dimensioni, tante dimensioni quanti parametri, e non siamo in grado di visualizzare o immaginare cose con più di 3 dimensioni.
Badate bene, la nuvola di punti esiste ed ha una sua forma anche se non riusciamo a vederla, e questa forma può comunque dare informazioni importanti su ciò che stiamo studiando. In genere alcuni valori dei parametri si presentano più frequentemente rispetto ad altri, quelli vicini alla media saranno più frequenti, di conseguenza capita quasi sempre che la maggior parte dei dati va ad addensarsi in “gruppetti” (meglio noti come cluster) ben delineati. I dati “distanti” dai cluster principali o comunque “isolati” rappresentano situazioni rare o anomale e riuscire a identificarli e comprenderli è di estrema importanza: potrebbero aiutare a predire l’insorgenza di una malattia, un uragano o un qualunque evento meteorologico straordinario, lo scoppio di una bolla speculativa e tanti altri eventi rari.

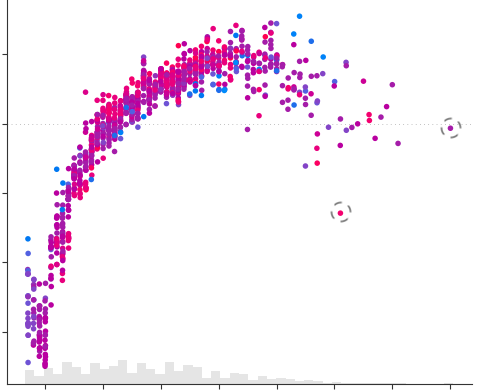Figura 2: I dati cerchiati in nero sono molto distanti dagli altri e quindi potrebbero rappresentare situazioni anomale. [2]

La forma della nuvola di dati racchiude quindi in sé informazioni cruciali. Ma come catturare la forma di un oggetto anche quando non riusciamo a visualizzarlo? Con l’omologia!
Una nuvola di punti si può trattare come uno spazio topologico e quindi possiamo calcolarne i gruppi di omologia. Il problema è che questo spazio topologico (almeno per ora) non ha una vera e propria forma, è fatto da tanti singoli punti staccati tra di loro, quindi i gruppi di omologia non danno chissà quali informazioni se non il numero di punti stesso. Si utilizza allora questa tecnica: si “gonfiano” i punti, cioè si creano dei cerchietti attorno a ciascun punto e li si ingrandiscono mano a mano, da una nuvola di punti otterremo così uno spazio “pieno”, con una forma più concreta. Non distinguiamo più i singoli punti ma solo i vari cerchietti, è come se offuscassimo la nostra vista, e appena due cerchietti iniziano a toccarsi non li distinguiamo più, diventano la stessa cosa. Man mano che ingrandiamo i cerchietti avremo sempre più sovrapposizioni, più i dati sono vicini e prima i rispettivi cerchietti si sovrapporranno, il nostro spazio inizierà ad assumere una forma sempre più delineata, e dopo un certo punto i cerchi saranno così grandi da ricoprire tutto lo spazio facendolo diventare una cosa unica. Con questo processo zone vicine si toccheranno fin da subito, si creeranno alcuni piccoli buchi che si richiuderanno poco dopo, mentre zone distanti o buchi più evidenti richiederanno più tempo per venire ricoperti. Le caratteristiche che “sopravvivono” (o meglio, persistono) più a lungo sono quelle più rilevanti, quelle che descrivono veramente la forma dell’oggetto e quindi quelle che ci interessano di più. La loro presenza è ben catturata dai gruppi di omologia, per questo motivo tale metodo è noto come omologia persistente.
L’omologia persistente è uno strumento nato abbastanza di recente e che stiamo ancora cercando di comprendere a fondo, ma che al tempo stesso si sta già rivelando molto potente in numerosi ambiti, dalla chimica all’astrofisica passando per il riconoscimento delle immagini. Se volete approfondirlo vi consiglio l’articolo di Massimo Ferri “L’incredibile ubiquità della topologia persistente“, che trovate sempre qui su Maddmaths!.

Figura 3: “Gonfiamento” progressivo della nuvola di punti in alto a sinistra. Notare che il buco centrale, una volta formatosi, persiste molto a lungo, bisogna gonfiare molto i cerchietti prima di farlo sparire, al contrario dei buchetti che si vengono a creare nella parte esterna. [3]

Mi dilungherò meno sulle prossime applicazioni della topologia, non perché ci sia meno da dire (anzi…) ma perché rischieremmo di parlare per ore. Tra tutti gli ambiti in cui si può applicare la topologia, quelli che forse sorprendono di più sono la robotica e la biologia. Che c’entra la topologia con i robot? E con la biologia poi?

Ad un robot, ma in generale ad ogni sistema meccanico, possiamo associare un particolare spazio topologico detto “spazio delle configurazioni“, che sostanzialmente tiene conto dei vincoli e dei gradi di libertà a cui il sistema è sottoposto. Per esempio lo spazio delle configurazioni di un braccio meccanico snodato in un punto come quello in figura 4 è il toro: ogni tratto del braccio può muoversi lungo una circonferenza, quindi complessivamente il sistema può essere trattato come una circonferenza che si muove su un’altra circonferenza, che topologicamente è equivalente a un toro (cioè il prodotto di due circonferenze). Il vantaggio è che questo spazio rappresenta da solo tutte le possibili configurazioni che potrà assumere il sistema, un singolo punto rappresenta una configurazione dell’intero oggetto, quindi studiando questo spazio riusciamo a capire in un colpo solo tutto quello che potrebbe fare il nostro robot. E giusto per ricollegarci alla scorsa puntata, lo spazio delle configurazioni è una varietà.

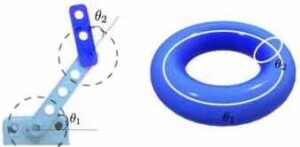Figura 4: Un braccio robotico a due tratti e il suo spazio delle configurazioni. [4]

Breve inciso: questo approccio è fondamentale nella fisica matematica per studiare il moto di corpi o l’evoluzione di interi sistemi soggetti a vincoli. Ogni punto dello spazio delle configurazioni (qui noto come spazio delle fasi) racchiude in sé tutte le informazioni su posizione, velocità e stato del sistema studiato, e l’evoluzione nel tempo di questo sistema (che può anche essere molto complessa) è perfettamente descritta dalla traiettoria di un punto che si muove nello spazio delle fasi.

Figura 5: Usando lo spazio delle fasi possiamo trattare una vasta gamma di sistemi dinamici, dal semplice pendolo o palla che rotola fino al moto di interi sistemi di pianeti e sistemi caotici. [5],[6]

Torniamo alla robotica. Immaginate di salire su una macchina a guida automatica e di dire “Portami a casa!”. Giustamente vorreste che questa macchina eviti i vari ostacoli che troverà inevitabilmente lungo il tragitto, sarebbe bello se la macchina fosse in grado di pianificare per bene il percorso e stare attenta a dove va. Questo problema è noto come “navigation problem” (problema della navigazione) e può essere attaccato usando la topologia: lo spazio in cui ci si può muovere tenendo conto di vincoli (come il bordo della strada) e ostacoli diventa uno spazio topologico e il tragitto diventa un arco in esso, cioè una curva continua. Andando a guardare le omotopie nello spazio ottenuto siamo in grado di studiare la stabilità dell’algoritmo di pianificazione di movimento, cioè la capacità di adattarsi a cambiamenti, per applicare poi eventuali correzioni. D’altra parte questo approccio ci ha anche fatto scoprire un nuovo interessante invariante omotopico per uno spazio \(X\) che abbiamo chiamato “complessità di navigazione”, solitamente indicato con \(TC(X)\). Questo invariante ci dice quanto è complicato muoverci dentro \(X\), e si dimostra che se due spazi hanno diversa complessità di navigazione allora non possono essere omeomorfi (e ricordate che capire se due spazi sono omeomorfi è l’obiettivo di fondo della topologia).
Non sempre è la matematica ad aiutare nelle applicazioni, a volte solo le applicazioni a farci scoprire qualcosa di nuovo nella matematica!

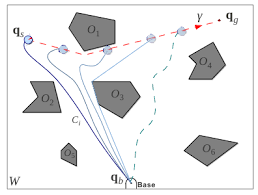Figura 6: Pianificazione del movimento in un percorso con ostacoli. [7]

Un biologo potrebbe non aver mai sentito parlare di topologia e sicuramente un topologo non sa nulla di biologia, ma recentemente alcune ricerche sono riuscite a costruire un ponte tra queste due discipline così apparentemente distanti. L’interazione tra proteine è uno dei processi fondamentali della biologia, è alla base del funzionamento di un sistema biologico e rende possibile il miracolo della vita. Per capire meglio come funziona questo magnifico e intricato processo sarebbe interessante saper predire quali proteine interagiranno con altre conoscendo solamente la loro forma e le forze in gioco tra i loro atomi. Tale problema è chiamato “protein docking problem” (che è molto più profondo di quanto non sarei in grado di spiegarvi) ed è noto per essere estremamente difficile. Parte della difficoltà è dovuta al fatto che le proteine e in generale le molecole non hanno una forma “rigida”, si piegano e si deformano, ma per fortuna la topologia studia proprio questo! Ovviamente la forma di una proteina o di una molecola non è sufficiente da sola per capire come interagirà con le altre e l’approccio topologico a questo problema non sembra ad ora essere il più promettente, ma è comunque molto interessante.

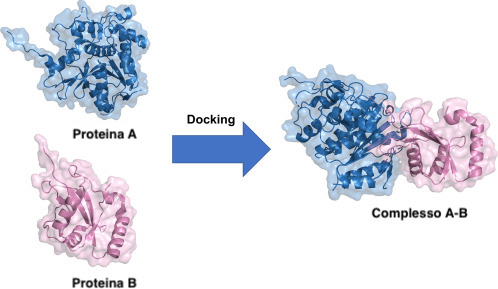Figura 7: Ogni proteina ha una propria forma e legandosi ad altre questa può deformarsi. [8]

Un altro frutto della topologia molto usato nella pratica è il grafo, che consiste in una serie di punti (detti vertici) collegati tra di loro tramite degli archi. Un grafo è un modello che si presta bene per varie situazioni: rapporti e commerci in politica economica, classificazione della specie in biologia, studio delle molecole in chimica, lo spargersi di una voce o una moda in sociologia, le amicizie in un social network e l’intero internet stesso e il collegamento tra i vari siti, e potremmo continuare ancora.
I grafi della topologia sono molto utili poiché non tengono conto della distanza tra i vertici ma solo di come essi sono collegati tra loro, sono molto “plastici”, come del resto ogni oggetto topologico.

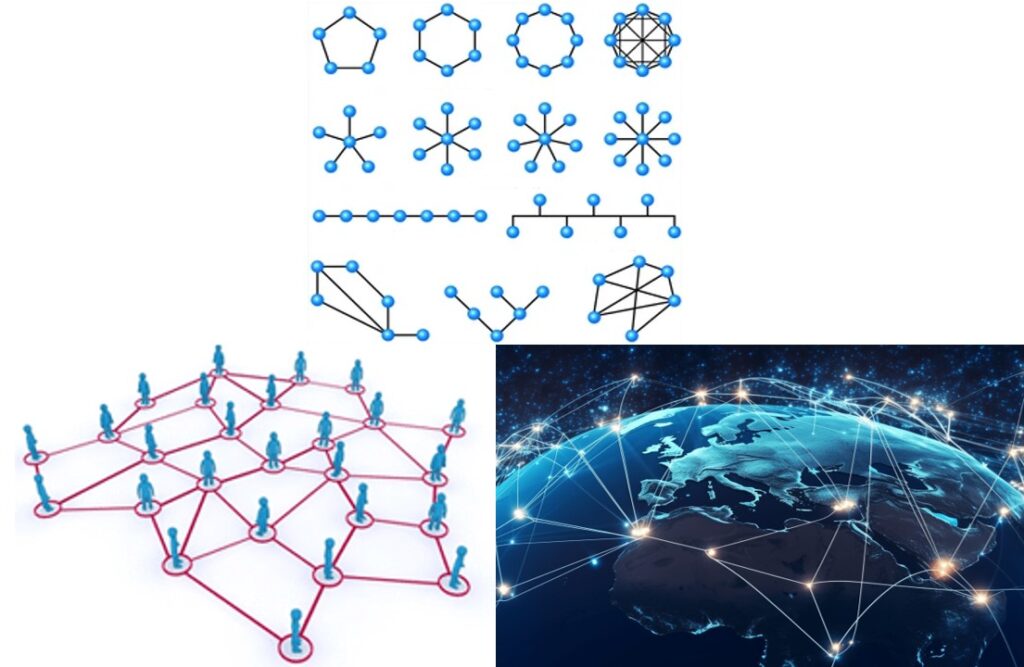Figura 8: In alto alcuni esempi di grafi, in basso si nota come i grafi sono modelli naturali per le interazioni tra individui e tra interi paesi. [9],[10],[11]

La nascita dell’idea di grafo è tradizionalmente associata al problema dei 7 ponti di Königsberg. Königsberg era una città della Prussia (oggi Kaliningrad in Russia) che sorgeva su entrambe sponde del fiume Pregel e includeva due isolotti e due porzioni principali collegate tra loro da 7 ponti. Il problema è quello di individuare un cammino che attraversi ogni ponte una e una sola volta.
Questo problema si presta benissimo ad essere trattato usando un grafo ed è evidente che non dipende né dalla lunghezza dei punti né dalla loro distanza ma solo da come essi collegano i vari punti della città. Fu risolto da Eulero nella prima metà del Settecento, che introdusse per primo l’idea di grafo e l’idea di indipendenza dalle distanze, e il suo lavoro è considerato come il primo tassello del domino che ha portato alla nascita della topologia. Comunqe la risposta al problema è no, non esiste un percorso che attraversa ogni ponte una e una sola volta (trovate qui una semplice spiegazione del perché).

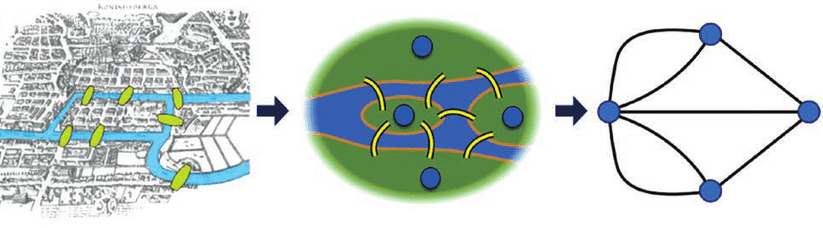Figura 9: Un grafo è un ottimo modello per schematizzare il problema dei ponti di Königsberg. [12]

Possiamo anche associare un peso ad ogni arco del grafo per distinguere i vari collegamenti tra di loro. L’oggetto che otteniamo è un grafo pesato, che viene ad esempio usato per trovare il percorso migliore tra due posti: la rete stradale è rappresentata dal grafo e il peso di ogni arco rappresenta la lunghezza di ogni strada, così il percorso più breve tra 2 posti sarà quello con minor peso totale nel grafo. Il peso di ogni arco potrebbe tener conto anche della presenza di eventuale traffico, ottimizzando ancora di più il percorso trovato.

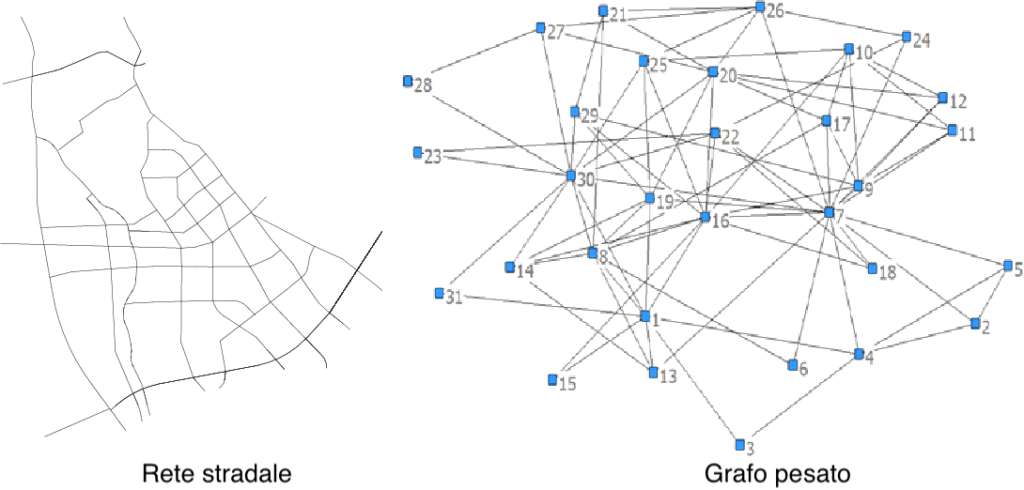Figura 10: Una rete stradale può essere trattata come un grafo pesato. Il numero che si trova all’inizio di ogni arco è il suo peso. [13]

Sempre i grafi pesati vengono usati come modello per le reti neurali, tra i programmi di intelligenza più importanti e che avete inconsapevolmente usato navigando fino a questo sito. Il nostro cervello è una macchina straordinaria e le reti neurali sono costruite cercando di imitarne lo schema, sono fatte da tanti neuroni che contengono le informazioni collegati da archi che ne permettono l’interazione. I neuroni sono i vertici del grafo, i collegamenti sono gli archi ed il loro peso è dato dalla “forza” di questo collegamento, cioè da quanto le informazioni contenute nei due neuroni vertici sono correlate tra loro.
Se masticate un po’ di inglese e siete interessati ad approfondire le reti neurali vi consiglio la bellissima serie di video a riguardo fatta da 3Blue1Brown, che grazie a delle splendide animazioni riesce a spiegare in modo incredibilmente chiaro, semplice e visuale gli aspetti principali delle reti neurali e del Machine Learning. La trovate su questo link.

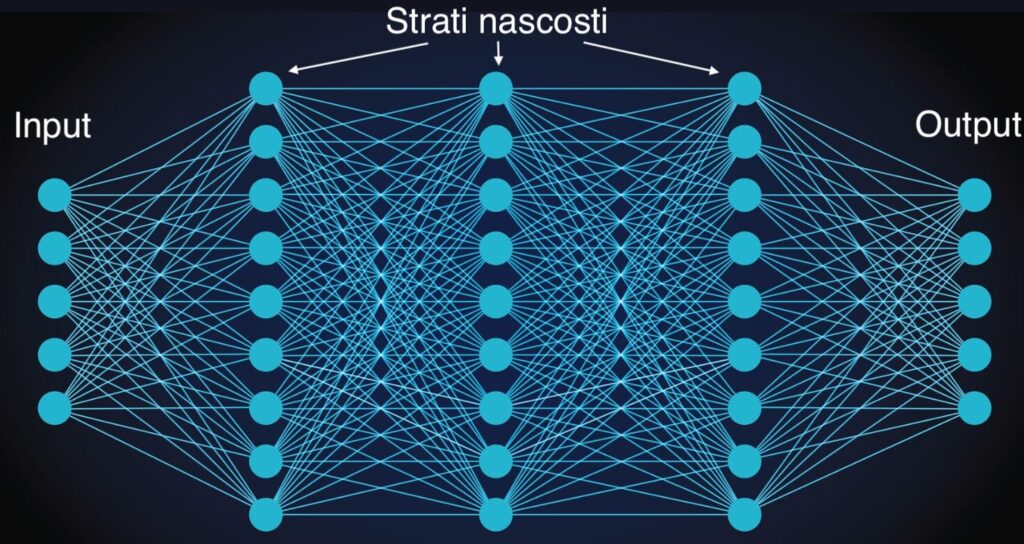Figura 11: Una rete neurale è un grafo a strati. Lo strato di input riceve i dati che vengono poi processati dagli strati nascosti (dentro i quali non abbiamo idea di cosa succeda, non sappiamo come ragiona il computer) e i risultati vengono mostrati nello strato di output. [14]

La topologia è incredibilmente vasta e ricca di teoremi. Alcuni di essi ci permettono di scoprire comportamenti sorprendenti del mondo che ci circonda, come il teorema di Borsuk-Ulam, una cui conseguenza è che in ogni istante ci saranno due punti opposti sulla Terra che avranno stessa temperatura e pressione atmosferica, o il teorema della sfera pelosa, che implica che sulla superficie della Terra ci sarà sempre almeno un punto in cui non soffia vento. Ci sono anche tanti altri teoremi che hanno importantissimi risvolti nelle branche più disparate della matematica: esempio principe è il teorema del punto fisso di Kakutani, che è stato riadattato e applicato da John Nash (sì, il Nash del film “A beautiful mind”) per descrivere il cosiddetto equilibrio di Nash. L’equilibrio di Nash descrive una situazione in cui più parti in competizione tra loro sono in uno stato in cui nessuna riesce a guadagnare nulla cambiando la propria strategia, generando quindi uno stallo, appunto un equilibrio. L’equilibrio di Nash è tra i concetti più utilizzati in teoria dei giochi – quella parte di matematica che si occupa di descrivere l’interazione cooperativa o non tra due o più parti, i giocatori, in un contesto in cui ognuno di loro vuole massimizzare il proprio guadagno – ed ha risvolti cruciali in economia e nello studio di interazioni strategiche, non a caso questo è valso a Nash il premio Nobel per l’economia. Inoltre, come visto nella scorsa puntata alcuni prodotti della topologia come le varietà sono molto utilizzati nella fisica, e sono addirittura alla base di intere teorie come quella della relatività generale.

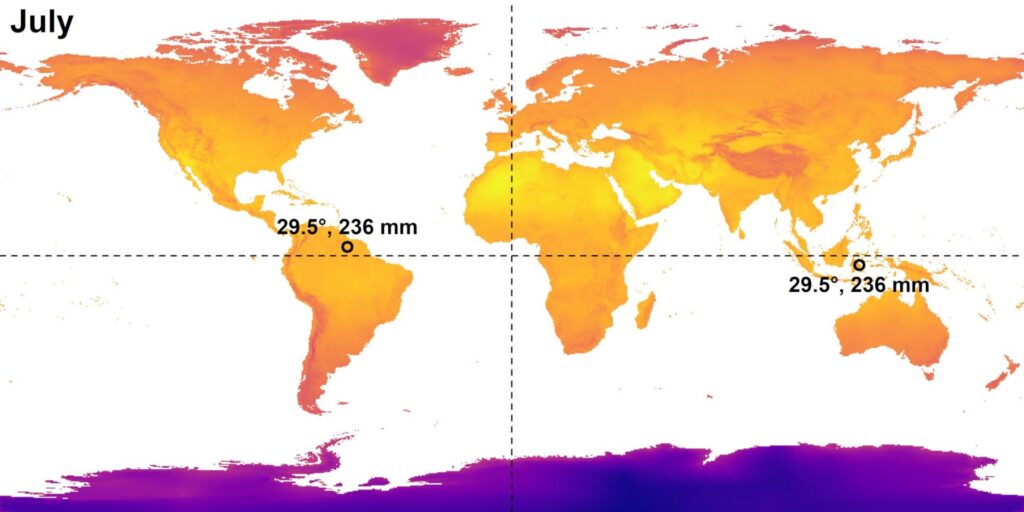Figura 12: Come stabilito dal teorema di Borsuk-Ulam ci sono due punti antipodali con stessa temperatura e pressione (qui anziché la pressione sono misurate le precipitaizioni, ma il principio dietro è lo stesso). [15]

Come vedete le applicazioni della topologia sono innumerevoli, quella che abbiamo visto oggi non è che la punta dell’iceberg, ma è meglio fermarci qui o rischieremmo di non finire più. Concludendo questo articolo concludiamo anche la serie “Una chiacchierata sulla topologia”: spero che sia stata piacevole, che abbiate scoperto qualcosa di nuovo o compreso meglio cose che già conoscevate, ma spero soprattutto di aver stimolato la vostra curiosità, che forse è la soddisfazione più grande per un divulgatore.
E’ stato un piacere!

 

Images credits:
Le copertine di questo articolo e degli altri della serie sono state realizzate da Nicolò Buselli.

[1] https://campus.datacamp.com/courses/exploratory-data-analysis-in-power-bi/relationships-between-continuous-variables?ex=2
[2] https://shap.readthedocs.io/en/latest/example_notebooks/api_examples/plots/scatter.html
[3] https://gjkoplik.github.io/pers-hom-examples/1d_pers_2d_data_widget.html
[4] https://mecharithm.com/learning/lesson/configuration-space-topology-representation-robot-5
[5] https://www.space.com/16080-solar-system-planets.html
[6] By Wikimol, Dschwen – Own work based on: images Lorenz system r28 s10 b2-6666.png by Wikimol and Lorenz attractor.svg by Dschwen, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=495592
[7] https://www.csc.kth.se/icra2016topology/sbhattacharya.pdf
[8] https://www.sciencedirect.com/topics/biochemistry-genetics-and-molecular-biology/protein-ligand-docking
[9] https://www.shutterstock.com/it/search/topology?image_type=vector
[10] https://www.davidealgeri.com/social-network-analysis/
[11] https://betanews.com/2024/01/01/why-enterprise-networks-need-to-move-to-an-as-a-service-model-qa/
[12] https://www.researchgate.net/figure/The-Konigsberg-bridge-puzzle-and-topologic-invariance-A-This-historical-problem-circa_fig1_324668123
[13] https://www.semanticscholar.org/paper/Analysing-the-Resilience-of-Road-network-in-Urban-Xu/4af531bb4ebaa84bfba05cc4d44013962e53b4d3
[14] https://aibusiness.com/ml/how-neural-networks-can-think-like-humans-and-why-it-matters
[15] https://scientificgems.wordpress.com/2021/06/28/the-borsuk-ulam-theorem/