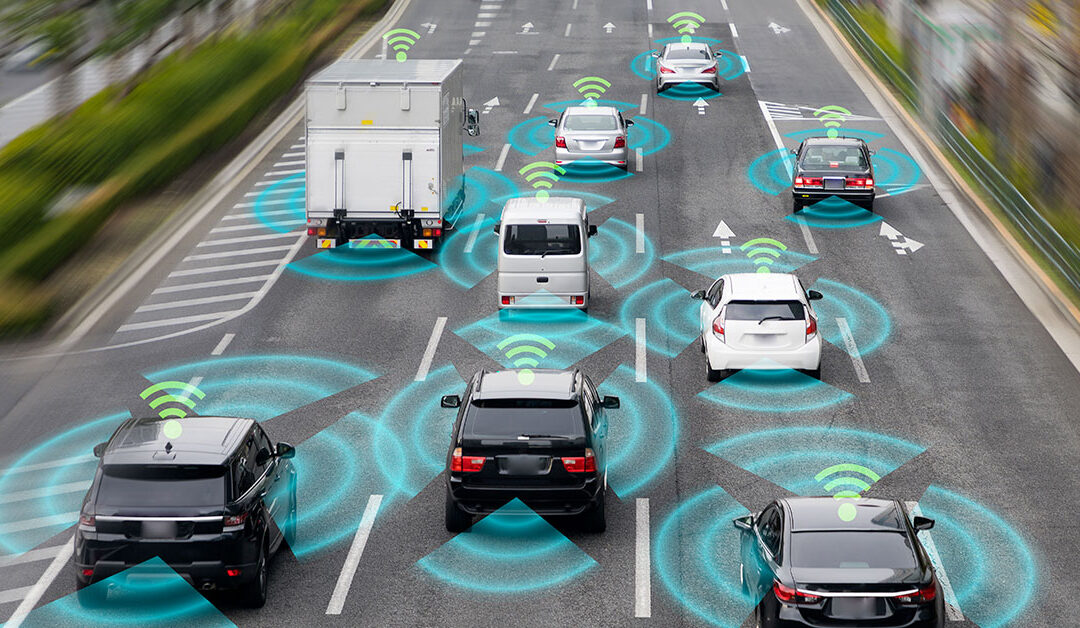
Gli scienziati utilizzano spesso la teoria dei giochi per capire in che modo i veicoli senza conducente riescano ad affrontare le situazioni complesse presentate dalla strada. Un ricercatore dell’Università della California di Santa Cruz, in particolare, ha lavorato a lungo su un sottoinsieme della teoria dei giochi che riguarda i cosiddetti “giochi differenziali”, che coinvolgono giocatori in movimento. In particolare, uno di questi giochi è chiamato “dell’inseguimento sul muro”: descritto per la prima volta negli anni Sessanta, in questo modello si ipotizza che un inseguitore più veloce debba catturare un fuggitivo, più lento, che è vincolato a muoversi lungo un muro. All’interno del gioco, sin dall’inizio, è stato individuato un “dilemma”, un insieme di posizioni in cui si pensava che non esistesse una soluzione ottimale per questo gioco.
Ora, Milutinovic e colleghi, in un nuovo articolo pubblicato sulla rivista IEEE Transactions on Automatic Control, hanno dimostrato che, invece, esiste sempre una soluzione deterministica al gioco dell’inseguimento sul muro. Questa conclusione consentirà di gestire meglio i sistemi autonomi come quelli coinvolti nei veicoli senza conducente (oltre che avere ricadute teoriche importanti su questioni similari nel campo della teoria dei giochi).

Uno dei concetti più noti della teoria dei giochi è l’equilibrio di Nash, che descrive le strategie di gioco ottimali che portano a concludere il gioco con i risultati migliori per tutti i giocatori. Se un giocatore sceglie di discostare la propria strategia da quella ottimale, finirà con un danno e quindi, in un gioco “razionale”, tutti sono motivati ad aderire alla strategia di equilibrio. Applicando l’equilibrio di Nash al gioco dell’inseguimento sul muro, per anni gli studiosi si sono trovati di fronte a un impasse: un insieme di posizioni di partenza (che costituivano la cosiddetta “superficie singolare”) in cui l’analisi classica non riusciva a fornire strategie ottimali. Da qui, il “dilemma”.

Per affrontare questo stallo, Milutinovic e colleghi hanno usato un concetto matematico che non esisteva quando il gioco dell’inseguimento sul muro è stato concepito. Sfruttando la soluzione della viscosità dell’equazione di Hamilton-Jacobi-Isaacs e introducendo un’analisi del tasso di perdita, hanno scoperto che è possibile determinare una strategia ottimale di gioco in ogni circostanza, sciogliendo così il dilemma.