di Serena Dipierro, Luca Lombardini, Pietro Miraglio e Enrico Valdinoci

L’Australia è un paese estremamente poetico e suggestivo, ben rappresentato da un inno nazionale allegro e cordiale, che canta cose come “Australiani gioiamo, perché siamo giovani e liberi”, “la nostra patria è circondata dal mare e abbonda dei doni della natura di una bellezza ricca e rara”, “lavoreremo alacremente con il cuore e le mani”, “per quelli che sono venuti attraverso i mari abbiamo illimitate pianure da condividere”, “con coraggio lasciateci collaborare, per promuovere l’Australia con giustizia”.
Anche l’ambiente universitario è pieno di brillanti scienziati che hanno attraversato i mari per arrivare quaggiù (tra i recenti acquisti dell’Università di Melbourne, ad esempio, ci sono americani, tedeschi, finlandesi, ecc. – e, ovviamente, italiani).

Tra i vari doni della natura, l’Australia è anche piena di animali incredibili, dai canguri ai koala, fino agli ornitorinchi, che sono così inverosimili che all’inizio tutti credevano fossero solo un pesce d’aprile. Tra gli abitanti dell’Australia venuti dal mare annoveriamo anche alcune comunità di pinguini che vivono nella parte meridionale dell’isola, e in effetti la marcia dei “piccoli pinguini” (il cui nome scientifico è “Eudyptula minor”) a Phillip Island è uno spettacolo da non perdere. Al tramonto, quando diventa troppo scuro per continuare a cacciare in mare, i pinguini escono dall’acqua per far ritorno alle loro tane, che sono piccole cavità nel terreno, a qualche decina di metri dalla riva. Ci sono vari video online che mostrano la marcia dei pinguini verso casa.
[youtube id=”yrUwMDHqNCE” width=”620″ height=”360″]

Ovviamente, nessun video può sostituire l’esperienza della sfilata dei pinguini dal vivo, quindi il lettore è cordialmente invitato a salpare i mari ed assistere all’evento di persona! Inoltre i video, per motivi pratici, talvolta si concentrano più sull’aspetto divertente e turistico della marcia, piuttosto che sull’evento in sé, che, oltre a essere estremamente suggestivo, offre allo spettatore matematico vari spunti di riflessione.
Così, alla fine della nostra gita, di rientro verso Melbourne nel bel mezzo della notte, abbiamo iniziato a pensare di nuovo a quello che avevamo visto e abbiamo cercato di comprendere la sfilata dei pinguini da un punto di vista “razionale”.

Guardando la sfilata, ci è sembrato che alcune semplici ma interessanti caratteristiche apparissero sistematicamente nel modo in cui i pinguini fanno ritorno a casa:

• Anzitutto, i pinguini hanno la forte tendenza a raggrupparsi in gruppi abbastanza numerosi sul bagnasciuga, prima di dirigersi tutti assieme verso le loro case;
• Una volta formato un gruppo abbastanza numeroso, i pinguini marciano compatti in linea retta verso la loro meta, alla velocità concessa dalla loro dondolante andatura;
• Al fine di formare questo gruppo, i pinguini si muovono avanti e indietro, in attesa di altri compagni, e possono anche decidere di tornare in acqua, se non hanno compagni sulla battigia;

Se, per caso o per sbaglio, un pinguino rimane isolato, può arrestarsi completamente (senza nessun apparente vantaggio dovuto a un tale comportamento). Questo tipo di arresto nella marcia e’ probabilmente abbastanza raro, tuttavia durante la sfilata che abbiamo visto dal vivo, è accaduto che un pinguino sia rimasto isolato: il pinguino in questione era assolutamente in forma dal punto di vista fisico e nulla gli impediva il movimento, tuttavia è rimasto bloccato per mezz’ora e il personale del Parco naturale è dovuto intervenire per salvarlo.

Per seguire il nostro istinto matematico (e per salvare il povero pinguino rimasto apparentemente “in preda al panico”), abbiamo così pensato di formulare un modello semplice ma rigoroso, basato su un sistema di equazioni differenziali ordinarie, che descrive la formazione dei gruppi di pinguini sulla battigia e la loro marcia verso casa.
I dettagli matematici possono essere letti nel nostro preprint “The Phillip Island penguin parade (a mathematical treatment)“, appena apparso su ArXiv [1].

La struttura matematica proposta prende in considerazione le seguenti funzioni:

• il numero di pinguini;
• la posizione di ogni pinguino (e di ogni gruppo di pinguini, una volta formati i gruppi);
• la vista del pinguino;
• l’ambiente esterno;
• una “funzione panico”.

La velocità di ogni pinguino è quindi determinata dall’ambiente esterno e da semplici considerazioni “strategiche” di questo tipo:

• se la distanza di un pinguino dagli altri è troppo grande, il pinguino va nel panico e si blocca (la sua velocità è allora determinata solo dall’ambiente esterno, e in caso di ambiente “neutrale” il pinguino resta completamente fermo);
• se la distanza di un pinguino dagli altri non è troppo grande, allora il pinguino “conta” i suoi compagni e ne valuta la distanza: cercherà allora di muoversi nella direzione in cui ci sono più pinguini, a minore distanza (notare che la funzione panico e la funzione vista sono “indipendenti”, cioè il pinguino potrebbe vedere alcuni compagni, ma giudicarli troppo distanti e quindi arrestarsi);
• con questa strategia, si formano dei gruppi di pinguini, in cui il numero dei componenti è via via crescente: quando il gruppo raggiunge un numero “sufficiente” di membri, allora decide di dirigersi a “passo sostenuto” (dal punto di vista pinguinesco) verso casa.

Piccole modifiche di questa versione possono tenere conto della volontà di qualche pinguino di lasciare un gruppo già formato (ad esempio, nel caso sia all’esterno del gruppo e si senta quindi più esposto al pericolo), dell’arrivo di un predatore, di un’onda più forte che “risucchi via” il pinguino dal bagnasciuga, ecc.

Il sistema di equazioni così ottenuto non è del tutto “standard” dal punto di vista matematico, perché, nel momento in cui un gruppo si forma, la teoria classica di Cauchy non può essere applicata, a causa della formazione di una singolarità. È però possibile risolvere facilmente questo problema con un metodo di “arresto e ripartenza” per l’equazione. Inoltre, si possono dimostrare alcuni risultati rigorosi sull’esito finale della sfilata dei pinguini e sul numero dei pinguini che riesce a far ritorno con successo alla propria tana.

Per favorire l’intuizione e permettere un confronto con il “mondo reale”, abbiamo anche presentato alcuni semplici programmi al computer che implementano numericamente l’equazione proposta e mostrano fenomeni come la formazione dei gruppi di pinguini e il possibile stato di panico.
Nei grafici che seguono, ad esempio, poniamo il tempo $$t$$ sull’asse delle ascisse, e lo spazio $$x$$ sull’asse delle ordinate. La tana dei pinguini è fissata al livello $$x=4$$ e il mare si estende nella regione $$x<0$$ (alcune onde possono però invadere la regione $$x>0$$ e influenzare il movimento dei pinguini anche sul bagnasciuga). Il gruppo considerato è di 20 pinguini, disposti al tempo $$t=0$$ nelle posizioni leggibili sul grafico.
Un primo esempio è il seguente:

Fin da subito i pinguini vanno ad unirsi, senza particolari incertezze. Una volta formatosi il gruppo vero e proprio, inizia la marcia compatta verso casa. Accanto a questo esempio di abilità e coordinazione pinguinesca c’è però la triste storia del pinguino partito più indietro: dopo un primo scatto in avanti, infatti, non riesce a raggiungere il gruppo, che anzi si allontana troppo, al punto da farlo entrare in panico. A questo punto è trascinato via dalle onde: un’onda più grande lo porta a riva, per poi riprenderselo tempo dopo. Ma il lettore non si disperi: i primi metri di oceano sono un luogo abbastanza sicuro per i pinguini (gli squali dovrebbero aggirarsi ben più al largo), sperabilmente il pinguino dimenticato potrà trovare altri compagni con cui arrivare a casa.

Diversa è la situazione del prossimo grafico, nel quale i pinguini sono inizialmente più sparpagliati rispetto al caso precedente.

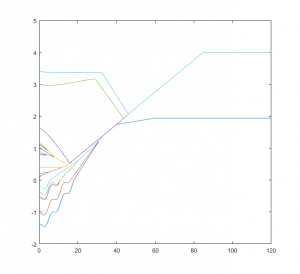
Si deve infatti pensare che l’arrivo dei pinguini sulla spiaggia avviene di continuo e ad ogni gruppo ne segue un altro alcuni minuti dopo, dunque i due pinguini più in alto potrebbero essere stati lasciati indietro da un precedente gruppo. Come ci possiamo aspettare, si forma progressivamente una compagine formata dalle 18 unità inizialmente più vicine: si osservi come i pinguini che partono più indietro rispetto allo zero (cioè in acqua) abbiano un percorso influenzato dalle onde. Si osservi anche il comportamento del pinguino colorato in verde: nei primissimi istanti si muove verso il basso, cercando un avvicinamento agli altri, ma dopo poco, quando questi si allontanano troppo, decide di ripiegare sul pinguino azzurro posto davanti a lui. In questo caso, un pinguino già unitosi agli altri lascia il gruppo: prima rallenta, probabilmente a causa di un agente esterno, poi va in panico e si blocca. Un caso simile ma a lieto fine è il seguente:

Come in precedenza si forma il gruppo, dal quale un pinguino per qualche ragione perde contatto. Anziché andare in panico e bloccarsi come il precedente, decide di fare ritorno velocemente in acqua, dove incontra un altro pinguino in balia delle onde fin dal tempo 0: ad un certo punto i due si incontrano e lentamente procedono verso casa, come mostrato nella parte finale del grafico. Questi grafici possono essere facilmente tradotti in semplici animazioni, come quelle disponibili su questa pagina.

L’ultima figura che proponiamo è quella di noi matematici pinguineschi durante una giornata lavorativa a Melbourne…

[1]

Serena Dipierro, Luca Lombardini, Pietro Miraglio, Enrico Valdinoci, The Phillip Island penguin parade (a mathematical treatment), preprint arXiv:1611.08715, 26 Nov 2016.