Una mini-serie a cura di Gabriele Belegni, dove esploreremo i concetti principali di una delle branche più affascinanti della matematica: la topologia. Cercheremo di scoprire le motivazioni e le idee che hanno spinto ad introdurre certi concetti concentrandoci sull’aspetto intuitivo piuttosto che su quello formale. Oggi impareremo come catturare delle caratteristiche geometriche di spazi anche molto complicati. Trovate tutte le puntate su questa pagina.

Riprendiamo da dove ci eravamo lasciati: stiamo facendo topologia, il che significa che vogliamo capire se degli spazi dati sono omeomorfi oppure no. Per farlo abbiamo introdotto le proprietà topologiche, e abbiamo visto che se due spazi topologici non condividono queste proprietà allora non possono essere omeomorfi. Le proprietà topologiche sono utilissime, ma non sufficienti.
Già, perché con esse non siamo ancora in grado di distinguere molti spazi, ad esempio non riusciamo a capire se un toro ed una sfera sono omeomorfi, nonostante la risposta sembra evidentemente essere un no: il toro ha un buco che la sfera non ha, quindi per deformare uno sull’altra dovremo richiudere questo buco, cioè incollarne i bordi, ma se si incolla non si ha un omeomorfismo, viceversa per deformare una sfera fino a renderla un toro dovremmo bucarla, cioè strapparla da qualche parte, e di nuovo non avremmo un omeomorfismo. Eppure sfera e toro condividono tutte le proprietà topologiche che abbiamo visto (e anche altre): sono entrambi compatti, connessi e \(T_4\), addirittura metrizzabili (cioè possiamo trovare un modo di misurare le distanze su di essi). Ci serve qualcos’altro per distinguerle.

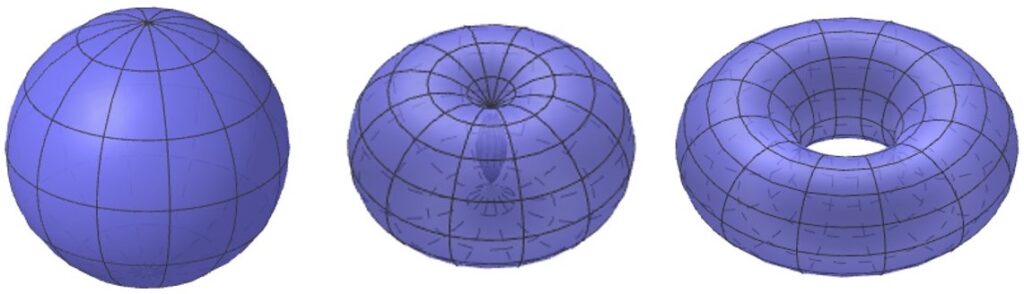
Figura 1: Non possiamo deformare una sfera (a sinistra) su un toro (a destra). Possiamo schiacciare i poli della sfera sempre di più, ma non riusciremo mai a ricreare il buco centrale senza strappare.

La presenza di buchi sembra essere una caratteristica importante, in effetti se due spazi hanno un numero di buchi diverso non possono essere omeomorfi, proprio perché per creare un buco bisogna commettere uno strappo, mentre per richiuderne uno bisogna incollarne il bordo, quindi gli omeomorfismi non possono modificare il numero di buchi. Questo numero sembra essere un ottimo candidato per essere una proprietà topologica, ma il problema è che quando ci viene dato uno spazio non abbiamo modo di capire quanti buchi ha, almeno con gli strumenti visti finora.
Certo, se lo spazio è molto semplice e riusciamo a disegnarlo su un foglio possiamo contarli, ma in generale gli spazi che ci capitano non possono essere disegnati e talvolta nemmeno immaginati in quanto hanno più di 3 dimensioni, è quindi impossibile contarne i buchi. Abbiamo bisogno di nuovi strumenti, nuove trasformazioni: ecco che incontriamo le omotopie.
Metto subito le mani avanti: di tutti i concetti che vedremo in questa serie, le omotopie sono senza dubbio il più vasto e formalmente complicato, per parlarne in modo semplice saremo quindi costretti a tralasciare vari aspetti tecnici, a volte commettendo piccolo imprecisioni.

La definizione rigorosa di omotopia richiede un po’ di formalismo che oggi eviteremo. Intuitivamente, in uno spazio topologico due archi (cioè due curve) con gli stessi estremi sono omotopi se possiamo deformare con continuità uno sull’altro rimanendo dentro lo spazio, eventualmente schiacciandoli o dilatandoli. Non stiamo più proibendo di incollare, ma solo di strappare, insomma abbiamo molta libertà. Detto in modo coinciso, due archi sono omotopi se possiamo deformare uno sull’altro senza romperli.

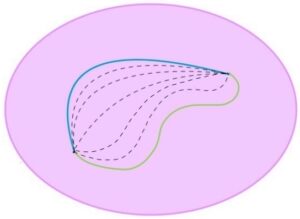
Figura 2: L’arco blu e quello verde sono omotopi. Il processo di deformazione è rappresentato dagli archi tratteggiati.

Gli archi a cui siamo interessati ora sono quelli che iniziano e finiscono nello stesso punto, i cosiddetti cappi. Immaginateli come degli elastici di gomma che possiamo piegare e allungare ma non vogliamo rompere.
In uno spazio senza buchi, ad esempio \(\mathbb{R}^2\) (il piano), è evidente che tutti i cappi che partono in uno stesso punto sono omotopi tra di loro ed omotopi al “cappio banale”, cioè al singolo punto da cui escono, detto punto base. Tutti i vari punti base possono poi essere collegati tra loro da archi, e questo rende in un certo senso equivalenti anche cappi che escono da punti base diversi. Uno spazio con queste caratteristiche è detto semplicemente connesso.
Questa cosa non accade più se lo spazio ha un buco: i cappi che passano attorno a questo buco non possono essere deformati su quelli che non lo racchiudono, per farlo bisognerebbe infatti passarvi sopra, cioè bisognerebbe uscire dallo spazio topologico in cui lavoriamo, e questo non possiamo farlo. In uno spazio bucato non tutti i cappi sono omotopi.

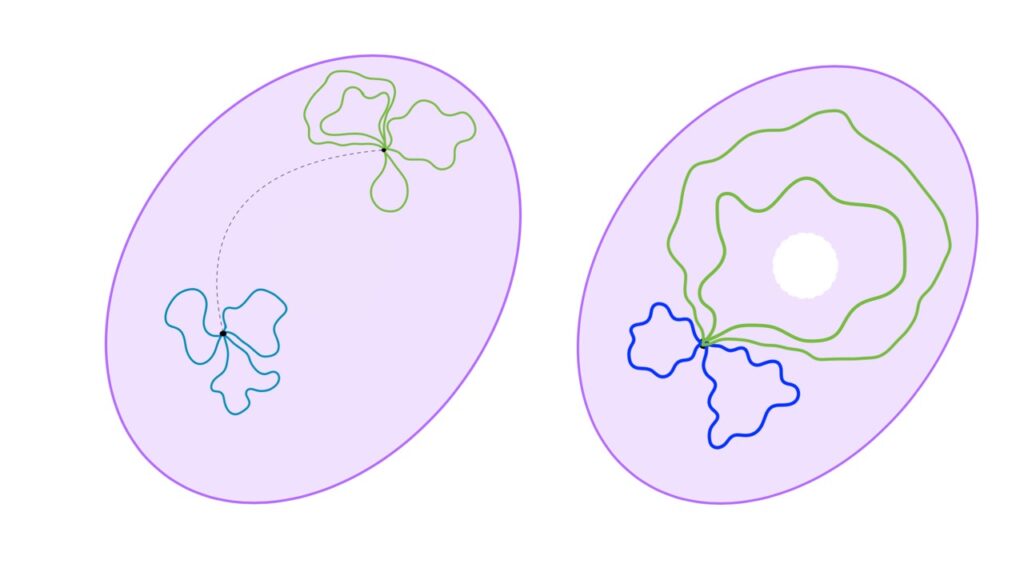 Figura 3: A sinistra uno spazio semplicemente connesso. Tutti i cappi con uno stesso punto base sono omotopi tra loro e i vari punti base possono essere collegati da un arco. A destra uno spazio con un buco. Gli archi verdi non sono omotopi a quelli blu a causa della presenza del buco.

Bene, ma la situazione non sembra molto migliore rispetto a prima… se lo spazio ha molte dimensioni non riusciamo a figurarcelo, quindi neanche a rappresentare i cappi su di esso, e come facciamo a capire se due cappi sono omotopi senza disegnarli? Non possiamo, quindi ci siamo inventati ancora un altro strumento: il gruppo fondamentale.
Nel gruppo fondamentale tutti i cappi omotopi tra loro diventano un singolo elemento, una cosa sola. Ecco, se in uno spazio topologico \(X\) non ci sono buchi, o meglio se è semplicemente connesso, tutti i cappi dentro di esso saranno omotopi, non c’è nulla che impedisce di deformare uno sull’altro, e quindi il gruppo fondamentale di \(X\) (indicato con \(\pi_1(X)\)) conterrà un solo elemento che li rappresenta tutti. Questo è il caso più semplice possibile, si dice infatti che qui il gruppo fondamentale è banale.
Immaginiamo ora che \(X\) sia una superficie, ad esempio un foglio di carta. Se \(X\) ha un buco, come detto sopra i cappi che vi passano attorno non sono omotopi a quelli che non lo racchiudono, quindi possiamo suddividere i cappi in 2 classi: quelli che racchiudono il buco, che saranno tutti omotopi tra loro, e quelli che non lo racchiudono, sempre omotopi tra loro ma non a quelli dell’altra classe. Di conseguenza il gruppo fondamentale di \(X\) avrà 2 elementi, uno per ciascuna di queste classi. La presenza di più elementi nel gruppo fondamentale è il segnale che ci sono buchi.

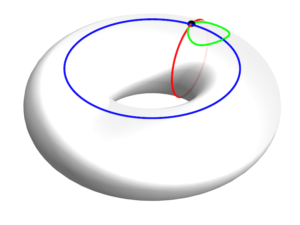Figura 4: Questi 3 archi nel toro non sono omotopi, di conseguenza il suo gruppo fondamentale ha almeno 3 elementi (in realtà sono esattamente 3). In effetti ci sono 2 buchi: quello centrale e quello “interno” (ricorda che il toro è una superficie con interno cavo, come un tubo con gli estremi incollati). [1]

I nomi non sono mai casuali: il gruppo fondamentale si chiama così proprio perché si comporta come un gruppo, uno degli oggetti più importanti di tutta la matematica e alla base dell’algebra. Non abbiamo tempo di definire precisamente i gruppi, per farla breve sono degli insiemi in cui possiamo fare un’operazione che soddisfa alcune semplici proprietà, ad esempio i numeri interi (0,1,-1,2,-2,…) formano un gruppo con l’operazione di addizione. Vi basti sapere che conosciamo molto bene come sono fatti e come si comportano i gruppi e sappiamo trattarli molto meglio rispetto agli spazi topologici, è quindi veramente comodo tradurre informazioni topologiche nel linguaggio dei gruppi, cosa che il gruppo fondamentale riesce a fare abbastanza bene.

Con un po’ di lavoro si dimostra poi che se due spazi hanno gruppi fondamentali diversi allora non possono essere omeomorfi (diversi nel senso specifico dell’algebra, cioè non isomorfi, ma sorvoliamo). Ottimo, sembra che il gruppo fondamentale sia lo strumento giusto per contare i buchi di uno spazio, e ci permette anche di distinguere spazi non omeomorfi, che è sempre stato il nostro obiettivo! Purtroppo anche questa volta le cose non sono così immediate.

Consideriamo una sfera. Ricordate che in topologia quando si parla di sfera la si intende sempre come superficie, quindi essa ha un buco, la cavità interna. Tuttavia, se ci mettessimo a disegnare dei cappi su una sfera ci accorgeremmo che possiamo sempre deformarli su un singolo punto, quindi tutti i cappi sono omotopi tra loro e al cappio banale, di conseguenza il gruppo fondamentale della sfera ha un solo elemento, è banale (figura 5). Ecco, il gruppo fondamentale non è riuscito a catturare la presenza del buco nella sfera, e se non ce l’ha fatta per la sfera figuriamoci per spazi più complicati!
In effetti si può dimostrare che la sfera è semplicemente connessa.
Qui si nasconde una delle tante sottigliezze formali che vi ho nascosto: il gruppo fondamentale è abbastanza bravo nel catturare la presenza di buchi, ma solo di buchi “1-dimensionali”, come quelli che potreste creare su un foglio di carta. La sfera ha invece un buco “2-dimensionale”, e il gruppo fondamentale \(\pi_1\) non riesce a vederlo. Per catturare la presenza di buchi di dimensione maggiore si usano altri “gruppi di omotopia”, che indichiamo con \(\pi_2, \pi_3, \dots\), ciascuno in grado di vedere buchi in dimensione via via maggiore. La presenza del buco della sfera \(S^1\) è ad esempio catturata da \(\pi_2(S^1)\). In generale uno spazio ha un buco \(n\)-dimensionale se e solo se il suo \(n\)-esimo gruppo di omotopia non è banale.
Questo ci consente finalmente di dimostrare quello che avevamo inizialmente intuito su sfera e toro: il gruppo fondamentale della sfera è banale mentre quello del toro non lo è, e di conseguenza questi due spazi non possono essere omeomorfi.

Figura 5: Tutti i cappi su una sfera si possono “richiudere”, contrarre in un punto. [2]

Bene, a questo punto ci resta solo da calcolare il gruppo fondamentale e gli altri gruppi di omotopia. Ecco, questo è un bel problema. Già, perché in generale il loro calcolo (e di conseguenza il conteggio dei loro elementi) è tutt’altro che facile, anzi, sono pochissimi gli spazi per cui sappiamo determinarli in modo soddisfacente.
Si introducono così i gruppi di omologia, uno strumento concettualmente più sofisticato ma il cui calcolo è estremamente più agevole rispetto a quello dei gruppi di omotopia. Preso uno spazio topologico \(X\), il suo primo gruppo di omologia, \(H_0(X)\), ci dice di quanti pezzi distinti è costituito \(X\) (più precisamente ci indica il numero delle sue componenti connesse per archi), il secondo gruppo di omologia, \(H_1(X)\), conta invece il numero di buchi 1-dimensionali di \(X\), \(H_2(X)\) conta il numero di buchi 2-dimensionali, \(H_3(X)\) i buchi tridimensionali e così via.
Anche i gruppi di omologia traducono informazioni topologiche nel più comprensibile linguaggio dei gruppi, e come dicevamo sono più semplici da calcolare rispetto a quelli di omotopia. Questa semplicità ha però un prezzo: i gruppi di omologia ci danno informazioni più “rozze” rispetto a quelle fornite dai gruppi di omotopia, inoltre la loro definizione formale risulta molto (molto) più complicata rispetto a quella dei gruppi di omotopia. Insomma, da una parte abbiamo informazioni poco raffinate ma “facili” da ottenere, dall’altra informazioni abbastanza precise ma difficili da ricavare.

Eravamo partiti cercando ci capire se due spazi sono omeomorfi o no, abbiamo notato che la presenza di buchi ci dà una grossa mano in questo senso e ci siamo così ritrovati con degli strani oggetti, dei gruppi. Siamo sconfinati nella topologia algebrica, quella parte di matematica che si occupa di usare strumenti dell’algebra per risolvere problemi di topologia. I gruppi di omotopia e di omologia sono dei cosiddetti invarianti algebrici di spazi topologici, nel senso che se due spazi topologici hanno gruppi di omologia o di omotopia diversi tra loro allora sicuramente non sono omeomorfi (ma non è detto che se tutti questi gruppi sono a due a due uguali allora gli spazi sono omeomorfi, insomma i gruppi vanno usati solo in senso esclusivo). Non sono esattamente delle proprietà topologiche, sono appunto dei gruppi, ma aiutano comunque a distinguere spazi.

Potremmo parlare di omotopie e omologie ancora per ore, ma penso sia meglio iniziare a concludere. Il conteggio dei buchi è solo uno dei numerosi aspetti che questi strumenti ci permettono di analizzare, potremmo ad esempio definire quando due interi spazi sono omotopi (e non solo gli archi di uno stesso spazio come fatto oggi), e di recente molti matematici si sono accorti che i gruppi di omologia possono rivelarsi molto utili nell’analisi dei dati. Per farla breve, i dati raccolti da un qualche esperimento possono essere trattati come uno spazio topologico le cui caratteristiche, catturate dai gruppi di omologia, possono dare informazioni sul comportamento (presente o futuro) del campione da cui i dati vengono raccolti. Questo approccio si sta rivelando utile in vari ambiti, dall’economia alla medicina, ma ve ne parlerò meglio nell’ultima puntata di questa serie, dove vedremo alcune delle numerose applicazioni della topologia al mondo reale.

Bene, per oggi abbiamo detto molte cose, è ora di salutarci. Ci vediamo nella prossima puntata, dove parleremo degli spazi topologici più usati e studiati: le varietà. A presto!

Image credits: [1] https://www.gregegan.net/DIDICOSM/Loops/Loops.html
[2] By Salix alba at English Wikipedia, CC BY 2.5, https://commons.wikimedia.org/w/index.php?curid=1972330